解三角形的实际应用 知识点题库
2022年冬奥会高山滑雪项目将在延庆小海坨山举行.小明想测量一下小海坨山的高度,他在延庆城区(海拔约500米)一块平地上仰望小海坨山顶,仰角15度,他向小海坨山方向直行3400米后,再仰望小海坨山顶,此时仰角30度,问小明测的小海坨山海拔约有 米.
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?

一只船自西向东匀速航行,上午10时到达灯塔P的南偏西75°距灯塔64海里的M处,下午2时到达这座灯塔东南方向的N处,则这只船航行的速度(单位:海里/小时)( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一艘轮船在江中向正东方向航行,在点P观测到灯塔A、B在一直线上,并与航线成角α(0°<α<90°),轮船沿航线前进b米到达C处,此时观测到灯塔A在北偏西45°方向,灯塔B在北偏东β(0°<β<90°)方向,0°<α+β<90° , 求CB;(结果用α,β,b表示)
如图,A、B两点都在河的对岸(不可到达),在河岸边选定两点C、D,测得CD=1000米,∠ACB=30°,∠BCD=30°,∠BDA=30°,∠ADC=60°,求AB的长.

如图,在平面四边形ABCD中,AD=1,CD=2,AC=  .
.
 .
. 
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣  ,sin∠CBA=
,sin∠CBA=  ,求BC的长.
,求BC的长.
如图,A,B两点在河的对岸,测量者在A的同侧选定一点C,测出A,C之间的距离是100米,∠BAC=105°,∠ACB=45°,则A、B两点之间为米.

一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟后,又测得灯塔S在货轮的东北方向,则货轮的速度为( )
A . 20(  +
+  )
B . 20(
)
B . 20(  ﹣
﹣  )
C . 20(
)
C . 20(  +
+  )
D . 20(
)
D . 20(  ﹣
﹣  )
)
 +
+  )
B . 20(
)
B . 20(  ﹣
﹣  )
C . 20(
)
C . 20(  +
+  )
D . 20(
)
D . 20(  ﹣
﹣  )
)
为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.

在△ABC中,角A,B,C所对的边分别为a.b.c,若A=60°,a=  ,b=
,b=  ,则B=( )
,则B=( )
 ,b=
,b=  ,则B=( )
,则B=( )
A . 30°
B . 45°
C . 135°
D . 45°或135°
某炮兵阵地位于  点,两个观察所分别位于
点,两个观察所分别位于  ,
,  两点,已知
两点,已知  为等边三角形,且
为等边三角形,且  ,当目标出现在
,当目标出现在  点(
点(  ,
,  两点位于
两点位于  两侧)时,测得
两侧)时,测得  ,
,  ,则炮兵阵地与目标的距离约为( )
,则炮兵阵地与目标的距离约为( )
 点,两个观察所分别位于
点,两个观察所分别位于  ,
,  两点,已知
两点,已知  为等边三角形,且
为等边三角形,且  ,当目标出现在
,当目标出现在  点(
点(  ,
,  两点位于
两点位于  两侧)时,测得
两侧)时,测得  ,
,  ,则炮兵阵地与目标的距离约为( )
,则炮兵阵地与目标的距离约为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,某河段的两岸可视为平行线  ,
,  .有一名学生为了测量该河段的宽度,他在河段的一岸边选取相距120米的
.有一名学生为了测量该河段的宽度,他在河段的一岸边选取相距120米的  、
、  两点,并观察对岸的点
两点,并观察对岸的点  ,测得
,测得  ,
,  .(
.(  )
)
 ,
,  .有一名学生为了测量该河段的宽度,他在河段的一岸边选取相距120米的
.有一名学生为了测量该河段的宽度,他在河段的一岸边选取相距120米的  、
、  两点,并观察对岸的点
两点,并观察对岸的点  ,测得
,测得  ,
,  .(
.(  )
) 
-
(1) 求线段
 的长度;
的长度;
-
(2) 求该河段的宽度.
东西向的铁路上有两个道口  、
、  ,铁路两侧的公路分布如图,
,铁路两侧的公路分布如图,  位于
位于  的南偏西
的南偏西  ,且位于
,且位于  的南偏东
的南偏东  方向,
方向,  位于
位于  的正北方向,
的正北方向,  ,
,  处一辆救护车欲通过道口前往
处一辆救护车欲通过道口前往  处的医院送病人,发现北偏东
处的医院送病人,发现北偏东  方向的
方向的  处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要
处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要  分钟,救护车和火车的速度均为
分钟,救护车和火车的速度均为  .
.
 、
、  ,铁路两侧的公路分布如图,
,铁路两侧的公路分布如图,  位于
位于  的南偏西
的南偏西  ,且位于
,且位于  的南偏东
的南偏东  方向,
方向,  位于
位于  的正北方向,
的正北方向,  ,
,  处一辆救护车欲通过道口前往
处一辆救护车欲通过道口前往  处的医院送病人,发现北偏东
处的医院送病人,发现北偏东  方向的
方向的  处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要
处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要  分钟,救护车和火车的速度均为
分钟,救护车和火车的速度均为  .
. 
-
(1) 判断救护车通过道口
 是否会受火车影响,并说明理由;
是否会受火车影响,并说明理由;
-
(2) 为了尽快将病人送到医院,救护车应选择
 、
、  中的哪个道口?通过计算说明.
中的哪个道口?通过计算说明.
管道清洁棒是通过在管道内释放清洁剂来清洁管道内壁的工具,现欲用清洁棒清洁一个如图1所示的圆管直角弯头的内壁,其纵截面如图2所示,一根长度为  的清洁棒在弯头内恰好处于
的清洁棒在弯头内恰好处于  位置(图中给出的数据是圆管内壁直径大小,
位置(图中给出的数据是圆管内壁直径大小,  ).
).
 的清洁棒在弯头内恰好处于
的清洁棒在弯头内恰好处于  位置(图中给出的数据是圆管内壁直径大小,
位置(图中给出的数据是圆管内壁直径大小,  ).
). 

-
(1) 请用角
 表示清洁棒的长L;
表示清洁棒的长L;
-
(2) 若想让清洁棒通过该弯头,清洁下一段圆管,求能通过该弯头的清洁棒的最大长度.
如图,某数学学习兴趣小组的同学要测量学校地面上旗杆CD的高度(旗杆CD垂直于地面),设计如下的测量方案:先在地面选定距离为30米的A, B两点,然后在A处测得  ,在B处测得
,在B处测得  ,
,  ,由此可得旗杆CD的高度为米,
,由此可得旗杆CD的高度为米,  的正切值为.
的正切值为.
 ,在B处测得
,在B处测得  ,
,  ,由此可得旗杆CD的高度为米,
,由此可得旗杆CD的高度为米,  的正切值为.
的正切值为. 
甲船在岛  的正南
的正南  处,以4千米/时的速度向正北方向航行,
处,以4千米/时的速度向正北方向航行,  千米,同时乙船自岛
千米,同时乙船自岛  出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
 的正南
的正南  处,以4千米/时的速度向正北方向航行,
处,以4千米/时的速度向正北方向航行,  千米,同时乙船自岛
千米,同时乙船自岛  出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
A .  B .
B .  C .
C .  D . 2.15h
D . 2.15h
 B .
B .  C .
C .  D . 2.15h
D . 2.15h
“伦敦眼”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,又称“千禧之轮”,该摩天轮的半径为6(单位:  ),游客在乘坐舱
),游客在乘坐舱  升到上半空鸟瞰伦敦建筑
升到上半空鸟瞰伦敦建筑  ,伦敦眼与建筑之间的距离
,伦敦眼与建筑之间的距离  为12(单位:
为12(单位:  ),游客在乘坐舱
),游客在乘坐舱  看建筑
看建筑  的视角为
的视角为  .
.
 ),游客在乘坐舱
),游客在乘坐舱  升到上半空鸟瞰伦敦建筑
升到上半空鸟瞰伦敦建筑  ,伦敦眼与建筑之间的距离
,伦敦眼与建筑之间的距离  为12(单位:
为12(单位:  ),游客在乘坐舱
),游客在乘坐舱  看建筑
看建筑  的视角为
的视角为  .
. 
-
(1) 当乘坐舱
 在伦敦眼的最高点
在伦敦眼的最高点  时,视角
时,视角  ,求建筑
,求建筑  的高度;
的高度;
-
(2) 当游客在乘坐舱
 看建筑
看建筑  的视角
的视角  为
为  时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑
时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑  的最低高度.
的最低高度. (说明:为了便于计算,数据与实际距离有误差,伦敦眼的实际高度为
 )
)
如图,曲柄连杆机构中,曲柄CB绕C点旋转时,通过连杆AB的传递,活塞做直线往复运动.当曲柄在CB0位置时,曲柄和连杆成一条直线,连杆的端点A在A0处.设连杆AB长200 , 曲柄CB长70
, 曲柄CB长70 , 则曲柄自CB0按顺时针方向旋转53.2°时,活塞移动的距离(即连杆的端点A移动的距离A0A)约为
, 则曲柄自CB0按顺时针方向旋转53.2°时,活塞移动的距离(即连杆的端点A移动的距离A0A)约为 .(结果保留整数)(参考数据:sin53.2°≈0.8)
.(结果保留整数)(参考数据:sin53.2°≈0.8)
 , 曲柄CB长70
, 曲柄CB长70 , 则曲柄自CB0按顺时针方向旋转53.2°时,活塞移动的距离(即连杆的端点A移动的距离A0A)约为
, 则曲柄自CB0按顺时针方向旋转53.2°时,活塞移动的距离(即连杆的端点A移动的距离A0A)约为 .(结果保留整数)(参考数据:sin53.2°≈0.8)
.(结果保留整数)(参考数据:sin53.2°≈0.8)
如图,经过城市 有两条夹角为60°的公路
有两条夹角为60°的公路 ,
,  , 实行垃圾分类政策后,政府决定在两条公路之间的区域内建造一座垃圾处理站
, 实行垃圾分类政策后,政府决定在两条公路之间的区域内建造一座垃圾处理站 , 并分别在两条公路边上建造两个垃圾中转站
, 并分别在两条公路边上建造两个垃圾中转站 ,
,  (异于城市
(异于城市 ),为方便运输,要求
),为方便运输,要求 (单位:km).设
(单位:km).设 .
.
 有两条夹角为60°的公路
有两条夹角为60°的公路 ,
,  , 实行垃圾分类政策后,政府决定在两条公路之间的区域内建造一座垃圾处理站
, 实行垃圾分类政策后,政府决定在两条公路之间的区域内建造一座垃圾处理站 , 并分别在两条公路边上建造两个垃圾中转站
, 并分别在两条公路边上建造两个垃圾中转站 ,
,  (异于城市
(异于城市 ),为方便运输,要求
),为方便运输,要求 (单位:km).设
(单位:km).设 .
.
-
(1) 当
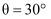 时,求垃圾处理站
时,求垃圾处理站 与城市
与城市 之间的距离
之间的距离 ;
;
-
(2) 当
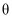 为何值时,能使得垃圾处理站
为何值时,能使得垃圾处理站 与城市
与城市 之间的距离最远?
之间的距离最远?
某兴起小组为了测量某古塔的高度,如图所示,在地面上一点A处测得塔顶B的仰角为60°,塔底C处测得A处的俯角为45°.已知山岭高CD为256米,则塔高BC为( )

A .  米
B .
米
B .  米
C .
米
C .  D .
D .  米
米
 米
B .
米
B .  米
C .
米
C .  D .
D .  米
米
最近更新
- 下列物质不能杀菌的是: A.苯酚溶液
- 已知△ ABC的两边方程是AB:5x-y-12=0,CA:x-5y+12=0,
- 如图,是一个圆柱体笔筒和一个正方体箱子.
- 一定条件下的密闭容器中:4NH3(g)+5O2(g)
- 材料一 孔子对晋铸刑鼎予以猛烈抨击:“晋
- 下列属于纯净物的是( ) A.合金 B.干冰 C
- 据《人民日报》报道,既不同于集体经济占主
- 分布在欧洲的人种主要是 A.黄色人种
- (本小题满分14分) 已知函数 . (1)解关于
- 欧州人多是白皮肤蓝眼睛,决定眼球颜色的结
- 观察下图,结合所学知识回答问题。 (1)、
- 如下图,这四位同学描述的可能同是下面的
- 可逆反应N2+3H2 2NH3的正、逆反应速率可用各反
- (08年哈三中理)已知等式成立,则 �
- 影响光合作用强度的环境因素包括 �
- 已知:如图,△DAC、△EBC均是等边三角形,点
- 在做“互成角度的两个力的合成”实验时,橡
- Professor Smith, along with his assistants,____ on the proje
- 如下图所示,水平轻弹簧与物体A和B相连,放
- 如图所示,假定一国现有资源用来生产两种产



