解三角形的实际应用 知识点题库
 , 若
, 若 , 则
, 则 的形状为( )
的形状为( )
A . 等腰三角形
B . 等腰直角三角形
C . 直角三角形
D . 等边三角形
在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:
方案﹣:直角顶点Q在斜边AB上,R,P分别在直角边AC,BC上;
方案二:直角顶点Q在直角边BC上,R,P分别在直角边AC,斜边AB上.请问应选用哪一种方案?并说明理由.

为了绘制海底地图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,A,B两点的距离为 海里.
海里.
(1)求△ABD的面积;
(2)求C,D之间的距离.

航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时),飞机先看到山顶的俯角为15°,经过420s(秒)后又看到山顶的俯角为45°,求山顶的海拔高度(取  ,
,  ).
).
 ,
,  ).
). 
在某次测量中,在A处测得同一方向的B点的仰角为60°,C点的俯角为70°,则∠BAC等于( )

A . 10°
B . 50°
C . 120°
D . 130°
在△ABC中,B=  ,BC边上的高等于
,BC边上的高等于  BC,则sinA=( )
BC,则sinA=( )
 ,BC边上的高等于
,BC边上的高等于  BC,则sinA=( )
BC,则sinA=( )
A . 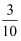 B .
B . 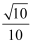 C .
C .  D .
D . 
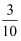 B .
B . 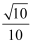 C .
C .  D .
D . 
为了测量灯塔AB的高度,第一次在C点处测得∠ACB=30°,然后向前走了20米到达点D处测得∠ADB=75°,点C,D,B在同一直线上,则灯塔AB的高度为.

某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:  ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73) 
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.

如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离.(计算结果精确到0.1km)参考数据:  ,
,  ≈2.45.
≈2.45.
 ,
,  ≈2.45.
≈2.45. 
如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E.

-
(1) 求BD2的值;
-
(2) 求线段AE的长.
某电力部门需在A、B两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离.现测量人员在相距  km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的
km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的  倍,问施工单位应该准备多长的电线?
倍,问施工单位应该准备多长的电线?
 km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的
km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的  倍,问施工单位应该准备多长的电线?
倍,问施工单位应该准备多长的电线? 
蓝军和红军进行军事演练,蓝军在距离  的军事基地
的军事基地  和
和  ,测得红军的两支精锐部队分别在
,测得红军的两支精锐部队分别在  处和
处和  处,且
处,且  ,
,  ,
,  ,
,  ,如图所示,则红军这两支精锐部队间的距离是 ( )
,如图所示,则红军这两支精锐部队间的距离是 ( )
 的军事基地
的军事基地  和
和  ,测得红军的两支精锐部队分别在
,测得红军的两支精锐部队分别在  处和
处和  处,且
处,且  ,
,  ,
,  ,
,  ,如图所示,则红军这两支精锐部队间的距离是 ( )
,如图所示,则红军这两支精锐部队间的距离是 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,一座建筑物AB的高为 (30-10  )m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为 ( )
)m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为 ( )
 )m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为 ( )
)m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为 ( ) 
A . 30 m
B . 60 m
C . 30 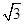 m
D . 40
m
D . 40 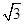 m
m
在地平面上有一旗杆 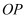 (
(  在地面),为了测得它的高度h,在地平面上取一长度为20m的基线
在地面),为了测得它的高度h,在地平面上取一长度为20m的基线  ,在A处测得P点的仰角为30°,在B处测得P点的仰角为45°,又测得
,在A处测得P点的仰角为30°,在B处测得P点的仰角为45°,又测得  ,则旗杆的高h等于m.
,则旗杆的高h等于m.
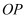 (
(  在地面),为了测得它的高度h,在地平面上取一长度为20m的基线
在地面),为了测得它的高度h,在地平面上取一长度为20m的基线  ,在A处测得P点的仰角为30°,在B处测得P点的仰角为45°,又测得
,在A处测得P点的仰角为30°,在B处测得P点的仰角为45°,又测得  ,则旗杆的高h等于m.
,则旗杆的高h等于m. 
俗语云:天王盖地虎,宝塔镇河妖.萍乡塔多,皆因旧时萍城多水患,民不聊生.迷信使然,建塔以辟邪镇邪.坐落在萍城小西门汪公潭境内的宝塔岭上就有这么一座“如愿塔”.此塔始建于唐代,后该塔曾因久失修倒塌,在清道光年间重建.某兴趣小组为了测量塔的高度,如图所示,在地面上一点A处测得塔顶B的仰角为  ,在塔底C处测得A处的俯角为
,在塔底C处测得A处的俯角为  .已知山岭高
.已知山岭高  为36米,则塔高
为36米,则塔高  为( )
为( )
 ,在塔底C处测得A处的俯角为
,在塔底C处测得A处的俯角为  .已知山岭高
.已知山岭高  为36米,则塔高
为36米,则塔高  为( )
为( ) 
A .  米
B .
米
B .  米
C .
米
C .  米
D .
米
D .  米
米
 米
B .
米
B .  米
C .
米
C .  米
D .
米
D .  米
米
如图,从气球  上测得正前方的河流的两岸
上测得正前方的河流的两岸  ,
,  的俯角分别为75°,30°,此时气球的高是
的俯角分别为75°,30°,此时气球的高是  ,则河流的宽度
,则河流的宽度  等于.
等于.
 上测得正前方的河流的两岸
上测得正前方的河流的两岸  ,
,  的俯角分别为75°,30°,此时气球的高是
的俯角分别为75°,30°,此时气球的高是  ,则河流的宽度
,则河流的宽度  等于.
等于. 
如图所示,为测量山高  选择A和另一座山的山顶
选择A和另一座山的山顶  为测量观测点,从A点测得
为测量观测点,从A点测得  点的仰角
点的仰角  点的仰角
点的仰角  以及
以及  从
从  点测得
点测得  ,若山高
,若山高  米,则山高
米,则山高  等于( )
等于( )
 选择A和另一座山的山顶
选择A和另一座山的山顶  为测量观测点,从A点测得
为测量观测点,从A点测得  点的仰角
点的仰角  点的仰角
点的仰角  以及
以及  从
从  点测得
点测得  ,若山高
,若山高  米,则山高
米,则山高  等于( )
等于( ) 
A . 300米
B . 360米
C . 240米
D . 320米
如图甲,首钢滑雪大跳台是冬奥历史上第一座与工业遗产再利用直接结合的竞赛场馆,大跳台的设计中融入了世界文化遗产敦煌壁画中“飞天”的元素.如图乙,某研究性学习小组为了估算赛道造型最高点A距离地面的高度AB(AB与地面垂直),在赛道一侧找到一座建筑物CD,测得CD的高度为h,并从C点测得A点的仰角为30°;在赛道与建筑物CD之间的地面上的点E处测得A点,C点的仰角分别为75°和30°(其中B,E,D三点共线).该学习小组利用这些数据估算得AB约为60米,则 的高h约为( )米
的高h约为( )米
 的高h约为( )米
的高h约为( )米(参考数据: ,
,  ,
,  )
)

A . 11
B . 20.8
C . 25.4
D . 31.8
江西浮梁地大物博,山清水秀;据悉,某建筑公司在浮梁投资建设玻璃栈道、摩天轮等项目开发旅游产业,考察后觉得当地两座山之间适合建造玻璃栈道,现需要测量两山顶M,N之间的距离供日后施工需要,特请昌飞公司派直升机辅助测量,飞机沿水平方向在A,B两点进行测量A,B,M,N在同一个铅垂平面内(如示意图).飞机测量的数据有在A处观察山顶M,N的俯角为: , 在B处观察山顶M,N的俯角为;
, 在B处观察山顶M,N的俯角为; , 飞机飞行的距离AB为
, 飞机飞行的距离AB为 , 请问:用以上测得的数据能否计算出两山顶间的距离MN,若能,请帮助该建筑公司求出MN,结果精确到
, 请问:用以上测得的数据能否计算出两山顶间的距离MN,若能,请帮助该建筑公司求出MN,结果精确到 , 若不能,请说明理由.
, 若不能,请说明理由.
 , 在B处观察山顶M,N的俯角为;
, 在B处观察山顶M,N的俯角为; , 飞机飞行的距离AB为
, 飞机飞行的距离AB为 , 请问:用以上测得的数据能否计算出两山顶间的距离MN,若能,请帮助该建筑公司求出MN,结果精确到
, 请问:用以上测得的数据能否计算出两山顶间的距离MN,若能,请帮助该建筑公司求出MN,结果精确到 , 若不能,请说明理由.
, 若不能,请说明理由.(参考数据: )
)

最近更新
- --Did you ask Jerry for help? -- I _____ need to --- I ma
- 判断下列连线题不正确的是
- 安德森认为“很多吊诡的是,前现代的帝国与
- 压强变化不会使下列化学反应的平衡发生移动
- It is a usual practice for Billy Crystal to keep _______toot
- 在空中喷洒干冰是人工增雨的一种方法。干冰
- 配制一定体积、一定物质的量浓度的溶液时,
- 国家实验室一个研小组发现首例带结晶水的晶
- 如图是周期表中短周期的一部分,A、B、C三种
- (1)至于夏水襄陵,____________。或王命急宣,有
- 在探究“影响电流热效应的因素”实验中:
- 如图所示为某一点电荷Q产生的电场中的一条
- 植物体细胞杂交的目的是( ) A.用酶解
- 某溶液中可能含有Na+、NH4+、Fe2+、K+、I-、SO
- 在汉武帝以后,儒学长期成为封建统治阶级的
- 《爱我中华》中有一句歌词说:“五十六个星
- 盛碱液的试剂瓶若使用磨口玻璃塞,时间长了
- These days my classmates are busy ____ ready for the gradu
- 矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,
- 某鱼贩一次贩运草鱼、青鱼、鲢鱼、鲤鱼及鲫



