解三角形的实际应用 知识点题库
如图,在倾斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的倾斜度为15°,向山顶前进100 m后,又从点B测得倾斜度为45°,假设建筑物高  ,设山坡对于地平面的倾斜度为
,设山坡对于地平面的倾斜度为  ,则
,则  ( ).
( ).

A .  B .
B .  C .
C .  D .
D . 
如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=(单位:m).

飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海波25000米,速度为3000米/分,飞行员先在点A看到山顶C的俯角为30°,经过8分钟后到达点B,此时看到山顶C的俯角为60°,则山顶的海拔高度为多少米.(参考数据:  =1.414,
=1.414,  =1.732,
=1.732,  =2.449).
=2.449).
 =1.414,
=1.414,  =1.732,
=1.732,  =2.449).
=2.449).
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=30米,并在点C测得塔顶A的仰角为60°,则塔高AB=米.

如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元.

-
(1) 设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
-
(2) 问中转站D建在何处时,运输总费用S最小?并求出最小值.
如图,CD是京九铁路线上的一条穿山隧道,开凿前,在CD所在水平面上的山顶外取点A,B,并测得四边形ABCD中,∠ABC=  ,∠BAD=
,∠BAD=  π,AB=BC=400米,AD=2米,求应开凿的隧道CD的长.
π,AB=BC=400米,AD=2米,求应开凿的隧道CD的长.
 ,∠BAD=
,∠BAD=  π,AB=BC=400米,AD=2米,求应开凿的隧道CD的长.
π,AB=BC=400米,AD=2米,求应开凿的隧道CD的长. 
如图,一栋建筑物AB的高为(30﹣10  )m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )
)m,在该建筑物的正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为( )

A . 30m
B . 60m
C . 30  m
D . 40
m
D . 40  m
m
 m
D . 40
m
D . 40  m
m
福州青运会开幕式上举行升旗仪式,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10  米,求旗杆的高度.
米,求旗杆的高度.
 米,求旗杆的高度.
米,求旗杆的高度.
在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进10  m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
 m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
m至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高. 
某舰艇在A处测得一遇险渔船在北偏东45°距离A处10海里的C处,此时得知,该渔船正沿南偏东75°方向以每小时9海里的速度向一小岛靠近,舰艇时速为21海里,求舰艇追上渔船的最短时间(单位:小时)
如图,OA、OB是两条公路(近似看成两条直线),  ,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N.
,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N.
 ,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N.
,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N. 
-
(1) 求纪念塔P到两条公路交点O处的距离;
-
(2) 若纪念塔P为小路MN的中点,求小路MN的长.
为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括:

-
(1) 指出需要测量的数据(用字母表示,并在图中标出);
-
(2) 用文字和公式写出计算山顶M海拔高度的步骤.
在三角形  中,角
中,角  及其对边
及其对边  满足:
满足:
 中,角
中,角  及其对边
及其对边  满足:
满足: .
.
-
(1) 求角
 的大小;
的大小;
-
(2) 求函数
 的值域.
的值域.
如图,一辆汽车在一条水平的公路上向正西行驶,到  处时测得公路北侧一山顶D在西偏北
处时测得公路北侧一山顶D在西偏北  的方向上,行驶600 m后到达
的方向上,行驶600 m后到达  处,测得此山顶在西偏北
处,测得此山顶在西偏北  的方向上,仰角为
的方向上,仰角为  ,则此山的高度
,则此山的高度  m.
m.
 处时测得公路北侧一山顶D在西偏北
处时测得公路北侧一山顶D在西偏北  的方向上,行驶600 m后到达
的方向上,行驶600 m后到达  处,测得此山顶在西偏北
处,测得此山顶在西偏北  的方向上,仰角为
的方向上,仰角为  ,则此山的高度
,则此山的高度  m.
m.
甲船在岛的正南方  处,
处,  千米,甲船以每小时4千米的速度向正北匀速航行,同时乙船自
千米,甲船以每小时4千米的速度向正北匀速航行,同时乙船自  出发以每小时6千米的速度向北偏东
出发以每小时6千米的速度向北偏东  的方向匀速航行,当甲、乙两船相距最近时,它们所航行的时间是( )
的方向匀速航行,当甲、乙两船相距最近时,它们所航行的时间是( )
 处,
处,  千米,甲船以每小时4千米的速度向正北匀速航行,同时乙船自
千米,甲船以每小时4千米的速度向正北匀速航行,同时乙船自  出发以每小时6千米的速度向北偏东
出发以每小时6千米的速度向北偏东  的方向匀速航行,当甲、乙两船相距最近时,它们所航行的时间是( )
的方向匀速航行,当甲、乙两船相距最近时,它们所航行的时间是( )
A . 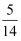 小时
B .
小时
B . 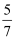 小时
C .
小时
C . 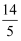 小时
D .
小时
D .  小时
小时
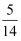 小时
B .
小时
B . 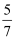 小时
C .
小时
C . 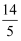 小时
D .
小时
D .  小时
小时
如图,某建筑物的高度  ,一架无人机
,一架无人机  上的仪器观测到建筑物顶部
上的仪器观测到建筑物顶部  的仰角为
的仰角为  ,地面某处
,地面某处  的俯角为
的俯角为  ,且
,且  ,则此无人机距离地面的高度
,则此无人机距离地面的高度  为
为 
 ,一架无人机
,一架无人机  上的仪器观测到建筑物顶部
上的仪器观测到建筑物顶部  的仰角为
的仰角为  ,地面某处
,地面某处  的俯角为
的俯角为  ,且
,且  ,则此无人机距离地面的高度
,则此无人机距离地面的高度  为
为 

如图,港口  在港口
在港口  的正东120海里处,小岛
的正东120海里处,小岛  在港口
在港口  的北偏东
的北偏东  的方向,且在港口
的方向,且在港口  北偏西
北偏西  的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口  出发,沿北偏东
出发,沿北偏东  的
的  方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口  .一艘给养快艇从港口
.一艘给养快艇从港口  以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛  ,在
,在  岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
 在港口
在港口  的正东120海里处,小岛
的正东120海里处,小岛  在港口
在港口  的北偏东
的北偏东  的方向,且在港口
的方向,且在港口  北偏西
北偏西  的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口  出发,沿北偏东
出发,沿北偏东  的
的  方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口  .一艘给养快艇从港口
.一艘给养快艇从港口  以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛  ,在
,在  岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时. 
-
(1) 求给养快艇从港口
 到小岛
到小岛  的航行时间;
的航行时间;
-
(2) 给养快艇驶离港口
 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
如图所示,为了测定河的宽度,在一岸边选定两点A,B,望对岸标记物C,测得  ,
,  ,
,  ,则河的宽度为.
,则河的宽度为.
 ,
,  ,
,  ,则河的宽度为.
,则河的宽度为. 
某人向正东走了x km后向右转了150°,然后沿新方向走3 km,结果离出发点恰好  km,那么x的值是( )
km,那么x的值是( )
 km,那么x的值是( )
km,那么x的值是( )
A .  B .
B .  C . 3
D .
C . 3
D .  或
或 
 B .
B .  C . 3
D .
C . 3
D .  或
或 
数学家研究发现,对于任意的  ,
,  ,称为正弦函数的泰勒展开式.在精度要求不高的情况下,对于给定的实数
,称为正弦函数的泰勒展开式.在精度要求不高的情况下,对于给定的实数  ,可以用这个展开式来求
,可以用这个展开式来求  的近值.如图,百货大楼的上空有一广告气球,直径为6米,在竖直平面内,某人测得气球中心
的近值.如图,百货大楼的上空有一广告气球,直径为6米,在竖直平面内,某人测得气球中心  的仰角
的仰角  ,气球的视角
,气球的视角  ,则该气球的高
,则该气球的高  约为米.(精确到1米)
约为米.(精确到1米)
 ,
,  ,称为正弦函数的泰勒展开式.在精度要求不高的情况下,对于给定的实数
,称为正弦函数的泰勒展开式.在精度要求不高的情况下,对于给定的实数  ,可以用这个展开式来求
,可以用这个展开式来求  的近值.如图,百货大楼的上空有一广告气球,直径为6米,在竖直平面内,某人测得气球中心
的近值.如图,百货大楼的上空有一广告气球,直径为6米,在竖直平面内,某人测得气球中心  的仰角
的仰角  ,气球的视角
,气球的视角  ,则该气球的高
,则该气球的高  约为米.(精确到1米)
约为米.(精确到1米) 
最近更新
- Bill Gates was born on October 28, 1955. He grew up in Seatt
- 如图,在正三角形中,,,分别是,,上的点
- 散文诗是介于诗与散文之间的一种文体,它采
- 读图4,回答13--14题。 13.甲、乙两区域共同
- 3.下列各句中,加横线的成语使用恰当的一
- —David, ______ you ______ your report?—No. I finished wr
- 将“挂绝壁松枯倒倚,落残霞孤鹜齐飞”(卢
- 世博会山东展馆的外形,体现了“海岱交融”
- 弗洛姆深刻地指出“19世纪的问题是上帝死了
- “沧海桑田”在地理科学上的含义( ) A
- CHICAGO (AP) On Jan. l,an order went into effect
- 每个时代,都有它特定的时代主题。在世界政
- 假如你是李华。你看到美国留学生Sharon 在网
- 函数的图象一定过定点__________.
- 已知某溶液中存在较多的H+、Ba2+、,则溶液中
- p{font-size:10.5pt;line-height:150%;margin:0;padding:0;}td{f
- 戴·克汽车公司曾宣布,将于2012年正式销售氢
- 完形填空 One Sunday afternoon,my younger brother and
- 中国特色文化建设的中心环节是( ) A.思
- 电视机的遥控器可以发射一种不可见光,叫做



