初中 数学
下列命题:①面积相等的两个三角形全等;②三角形三条高所在的直线交于一点;③等腰三角形两底角的平分线相等;④等腰三角形边上的高、中线和对角的平分线互相重合.其中真命题有( )个.
A . 1
B . 2
C . 3
D . 4.
某风景区的门票价格如下表所示:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
票价 | 100元/人 | 80元/人 | 50元/人 |
某校七年级甲、乙两班共100多人去该公园举行联欢活动,其中甲班50多人,乙班不足50人.如果以班为单位分别买票,两个班一共应付9200元;如果两个班联合起来作为一团体购票,一共只要付5150元.问:甲、乙两班分别有多少人?
不等式y+2≤3的正整数解为( )
A . 1,2
B . 2,3
C . 2
D . 1
下列计算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
长度分别为  ,
, 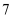 ,
,  的三条线段能组成一个三角形,
的三条线段能组成一个三角形,  的值可以是( )
的值可以是( )
 ,
, 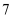 ,
,  的三条线段能组成一个三角形,
的三条线段能组成一个三角形,  的值可以是( )
的值可以是( )
A .  B .
B .  C .
C .  D .
D . 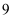
 B .
B .  C .
C .  D .
D . 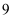
x=时,式子 与
与 互为相反数.
互为相反数.
 与
与 互为相反数.
互为相反数.
找出以下图形变化的规律,则第2016个图形中黑色正方形的数量是( )
![]()
A . 3021
B . 3022
C . 3023
D . 3024
观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.


与图形(1)相似的有;(填序号)
与图形(2)相似的有;
与图形(3)相似的有.
如图,三角形A′B′C′是由三角形ABC经过某种平移得到的,点A与点A′,点C与点C′分别对应,且这六个点都在格点(小正方形的顶点)上,解答下列问题:

-
(1) 分别写出点A和点A′的坐标,并说明三角形A′B′C′是由三角形ABC经过怎样的平移得到的.
-
(2) 连接BC′,∠CBC′与∠B′C′O之间的数量关系为.
-
(3) 若M(a﹣2,2b﹣3)是三角形ABC内一点,它随三角形ABC按(1)(2a﹣7,9﹣b),分别求a和b的值.
-
(4) 三角形A′B′C′的面积为.
下列方程的变形,正确的是( )
A . 由  ,得
,得  B . 由
B . 由  ,得
,得  C . 由
C . 由  ,得
,得 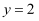 D . 由
D . 由  ,得
,得 
 ,得
,得  B . 由
B . 由  ,得
,得  C . 由
C . 由  ,得
,得 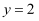 D . 由
D . 由  ,得
,得 
化简:(8x3y3﹣4x2y2)÷2xy2=.
京剧是我国的国粹,剪纸是流传已久的民间艺术,这两者的结合无疑是最能代表中国特色的艺术形式之一.图中京剧脸谱剪纸中是轴对称图形的个数是( )

A . 1个
B . 2个
C . 3个
D . 4个
使分式  等于0的x的值是( )
等于0的x的值是( )
 等于0的x的值是( )
等于0的x的值是( )
A . 1
B .  C .
C .  D . 不存在
D . 不存在
 C .
C .  D . 不存在
D . 不存在
某一次函数图象过点(﹣1,5),且函数y的值随自变量x的值的增大而增大,请你写出一个符合上述条件的函数关系式.
已知命题:“如图,点B、F、C、E在同一条直线上,则AB∥DE.”判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,在不添加其他辅助线的情况下,请添加一个适当的条件使它成为真命题,并加以证明.

已知关于  的方程
的方程  是一元二次方程,则m的取值范围是( )
是一元二次方程,则m的取值范围是( )
 的方程
的方程  是一元二次方程,则m的取值范围是( )
是一元二次方程,则m的取值范围是( )
A .  B .
B .  C .
C .  D . 任意实数
D . 任意实数
 B .
B .  C .
C .  D . 任意实数
D . 任意实数
如图,已知△ABC,请用尺规在BC的下方求作∠CBD,使得∠CBD=∠ACB.(保留作图痕迹,不写作法)

据统计,全球每分钟有8500000吨污水排入江河湖海,用科学记数法表示为
如图,已知Rt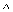 ABC中,∠C=90°
ABC中,∠C=90°
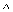 ABC中,∠C=90°
ABC中,∠C=90°
-
(1) 请按如下要求完成尺规作图(不写作法,保留作图痕迹)
①作∠BAC的角平分线AD,交BC于点D
②作线段AD的垂直平分线EF与AB相交于点O
③以点O为圆心,以OD长为半径画圆,交边AB于点M.
-
(2) 在(1)的条件成立下,若AM=3BM,AC=16,求圆O的半径.
菱形 ABCD 的周长为 24,其相邻两内角的度数比为  ,则此菱形的面积为( )
,则此菱形的面积为( )
 ,则此菱形的面积为( )
,则此菱形的面积为( )
A . 18
B . 18  C . 24
D . 9
C . 24
D . 9 
 C . 24
D . 9
C . 24
D . 9 
最近更新
- 雾凇通称“树挂”,其形成过程是:空气中湿
- 阅读下面语段,完成1—4题。 亮躬耕陇亩,好
- 一边吃东西一边说笑时,食物容易误入气管的
- 纵观哲学发展的历史,存在的两个对子是:
- 由于受日本大地震的影响,国内出现了抢购“
- 3.在下列语段横线处依次填入的句子,衔接
- 一个从静止开始作匀加速直线运动的物体,从
- 走进A省某市群众工作局大门时首先映入眼帘
- 决定化学反应速率的本质因素是( ) A.浓度
- 据报道,科学家成功制得了CO2的原子晶体(以
- 写作
- 张生在街口昕完说书后,又在自己居住的街区
- (1)如图(a),两个相同密闭盛水容器装有
- 如图是二氧化碳循环的部分过程。 该循环中
- 关于下列图示的说法错误的是 A.图一所
- 小明家厨房有一瓶失去标签的无色液体,妈妈
- In New York, students at 18 schools participate in a
- 分解因式:x2+2xy+y2=
- 2010年1月17日,中国八名维和警察在海地地震
- 质量为0.3kg的物体在水平面上运动,图中的



