初中 数学
如图,已知  中,
中,  =8,
=8,  =6,点
=6,点  是线段
是线段  的中点,点
的中点,点  在线段
在线段  上,若
上,若  与
与  相似,求
相似,求  的长.
的长.
 中,
中,  =8,
=8,  =6,点
=6,点  是线段
是线段  的中点,点
的中点,点  在线段
在线段  上,若
上,若  与
与  相似,求
相似,求  的长.
的长. 
小芳说:“我的矩形面积为6.”小丽说:“我的矩形周长为6.”下面说法错误的是( ).
A . 小芳:我的矩形一组邻边满足反比例函数关系,你的矩形一组邻边满足一次函数关系
B . 小丽:你的矩形周长不可能是6,我的矩形面积也不可能是6
C . 同学小文:你们的矩形都可能是正方形
D . 同学小华:小丽的矩形面积没有最大值
右边有两个大小形状完全相同的直角三角形,请你在平面上把这两个三角形拼出所有不同形状的四边形,并画出所拼四边形的示意图(标出图中的直角).

若x=1是方程mx2+3x+n=0的根,求(m﹣n)2+4mn的值.
计算: 

无论  取什么值,下列代数式中,值一定是正数的是( )
取什么值,下列代数式中,值一定是正数的是( )
 取什么值,下列代数式中,值一定是正数的是( )
取什么值,下列代数式中,值一定是正数的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
有理数3.645精确到百分位的近似数为( )
A . 3.6
B . 3.64
C . 3.7
D . 3.65
在实数1、0、﹣1、﹣2中,最小的实数是( )
A . ﹣2
B . ﹣1
C . 1
D . 0
如图,B、F、E、C四点在同一条直线上,AB=CD,AE=DF,CE=FB,判断∠B与∠C的关系,并证明.

计算:2﹣1+|﹣5|﹣sin30°﹣  .
.
 .
.
小明用计算器计算(a+b)c的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知a是b的3倍,则正确的结果是( )
A . 24
B . 39
C . 48
D . 96
在平面直角坐标系中,点  关于x轴的对称点的坐标是( )
关于x轴的对称点的坐标是( )
 关于x轴的对称点的坐标是( )
关于x轴的对称点的坐标是( )
A .  B .
B .  C .
C .  D .
D . 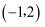
 B .
B .  C .
C .  D .
D . 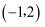
如图,在  中,
中,  ,将
,将  绕点
绕点  逆时针旋转
逆时针旋转  得到
得到  连接
连接  ,则
,则  的长为.
的长为.
 中,
中,  ,将
,将  绕点
绕点  逆时针旋转
逆时针旋转  得到
得到  连接
连接  ,则
,则  的长为.
的长为. 
除夕夜,父母给自己的一双儿女发压岁钱,先每人发了200元,然后在三个红包里面分别装有标有100元,300元,500元的卡片,每个红包和卡片除数字不同外,其余均相同,妹妹从三个红包中随机抽取了一个红包,记录数字后放回洗匀,哥哥再随机抽取一个红包,请用列表法或画树状图的方法,求父母给自己的一双儿女发压岁钱总和大于800元的概率.
如图,已知二次函数y=ax2+  x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
 x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
-
(1) 请直接写出二次函数y=ax2+
 x+c的表达式;
x+c的表达式;
-
(2) 判断△ABC的形状,并说明理由;
-
(3) 若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
-
(4) 若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
如图①,半径为R,圆心角为n°的扇形面积是S扇形= ,由弧长l=
,由弧长l= ,得S扇形=
,得S扇形= =
= •
• •R=
•R= lR.通过观察,我们发现S扇形=
lR.通过观察,我们发现S扇形= lR类似于S三角形=
lR类似于S三角形= ×底×高.
×底×高.
类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分交作扇环)的面积公式及其应用.

-
(1)
设扇环的面积为S扇环 ,
 的长为l1 ,
的长为l1 ,  的长为l2 , 线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=
的长为l2 , 线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形= ×(上底+下底)×高,用含l1 , l2 , h的代数式表示S扇环 , 并证明;
×(上底+下底)×高,用含l1 , l2 , h的代数式表示S扇环 , 并证明; -
(2) 用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?
下列图形中,是轴对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
空调安装在墙上时,一般都会象如图所示的方法固定在墙上,这种方法应用的数学知识是.

如图,  是两根木条,用
是两根木条,用  两根钉子钉在墙上,其中木条
两根钉子钉在墙上,其中木条  可以绕点
可以绕点  转动,木条
转动,木条  被固定不动.这一生活现象用你学过的数学知识解释为.
被固定不动.这一生活现象用你学过的数学知识解释为.
 是两根木条,用
是两根木条,用  两根钉子钉在墙上,其中木条
两根钉子钉在墙上,其中木条  可以绕点
可以绕点  转动,木条
转动,木条  被固定不动.这一生活现象用你学过的数学知识解释为.
被固定不动.这一生活现象用你学过的数学知识解释为. 
在  中,
中,  ,
,  ,将线段
,将线段  绕点
绕点 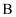 逆时针旋转
逆时针旋转  得到线段
得到线段  .
.
 中,
中,  ,
,  ,将线段
,将线段  绕点
绕点 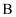 逆时针旋转
逆时针旋转  得到线段
得到线段  .
. 
-
(1) 如图①,直接写出
 的大小(用含
的大小(用含  的式子表示);
的式子表示);
-
(2) 如图②,
 ,
,  ,判断
,判断  的形状并加以证明.
的形状并加以证明.
最近更新
- 已知向量,,,且,则的值分别为 A. ,1 B.,2 C.
- 如图9所示的图象表示做直线运动的某一物体在0~5 s内的运动情况,由于画图人粗心未标明此图是v-t图还是x-t图,但已知
- 下列句子中标点符号使用正确的一项是( ) A.2006年5月1日,温家宝来到首钢餐厅,他对工人们说,今天是“五一”
- 下图是小华同学用氢氧化钠固体和水配制500g溶质质量分数2.5%的NaOH溶液的操作过程,该同学在称量氢氧化钠时,先将天
- 1.下列词语中加横线的字,注音全都正确的一项是 A.脖颈(jǐng) 蹙缩(cù) 喧阗(tián)
- 现有三组混合物:①乙酸乙酯和乙酸钠溶液 ②乙醇和丁醇 ③溴化钠和单质溴的水溶液,分离以上各混合物的正确方法依次为(
- (08年安庆市三模)阅读下面的文字,完成5―7题。和而不同 中国文化的基本特质是追求人与自然、人与人、人与自我的普
- 如图所示,物体A和B的质量分别为2kg和1kg,用跨过定滑轮的细线相连,静止地又叠放在倾角为=300的光滑斜面上,A与B
- 下列说法中,错误的是( )A.氧原子的半径比氮原子小B.氯原子的最外层电子数比硫原子的多C.金属钠投入氯化镁溶液中
- 建国62年、建党90年来,中华大地沧桑巨变,其原因有 () ①坚持了中国特色社会主义
- 为探究物质的燃烧条件,某同学进行了如图所示的实验,下列有关说法正确的() A、现象①③说明物质燃烧需要达到一定的温度 B
- 如图6所示,为了捉到一条鱼,猩猩用矛拼命地刺向水里却没有成功.这主要是由于光的_______现象.猩猩看到水中的鱼比实际
- (2011•淮安)如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点A按逆时针方向旋转15°后得
- 若|a+b|=|a-b|=2|a|,则向量a+b与a的夹角为()
- 如图是某森林生态系统碳循环示意图。甲、乙、丙、丁代表系统的不同成分,以下说法正确的是( )A、甲通过某项生理活动将
- 已知双曲线的一条渐近线为,则该双曲线的离心率为 A. B. C. D.
- 已知函数f(x)=xex(e为自然对数的底数).(1)求函数f(x)的单调递增区间;(2)求曲线y=f(x
- 使5.6 L CO2气体迅速通过Na2O2固体后得到4.48 L(标准状况下)气体,这4.48 L气体的质量为(
- 13.阅读下面这首词,回答问题。 采桑子 【清】纳兰性德 谁翻乐府凄凉曲?风也萧萧,雨也萧萧,瘦尽灯花又一宵。 不知何事
- 电饭锅工作时有两种状态:一种是锅内水烧干前的加热状态,另一种是锅内水烧干后的保温状态.图5-3-14所示是电饭锅电路的示



