初中 数学
如图所示,观察下面的国旗,是轴对称图形的是( )。 
A . (1)(2)(3)
B . (1)(2)(4)
C . (2)(3)(4)
D . (1)(3)(4)
平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为(0,0)、A(a,0)、C(0,b),且a、b满足  .
.
 .
. 
-
(1) 矩形的顶点B的坐标是.
-
(2) 若D是OC中点,沿AD折叠矩形OABC使O点落在E处,折痕为DA,连CE并延长交AB于F,求直线CE的解析式;
-
(3) 将(2)中直线CE向左平移
 个单位交y轴于M,N为第二象限内的一个动点,且∠ONM=135°,求FN的最大值.
个单位交y轴于M,N为第二象限内的一个动点,且∠ONM=135°,求FN的最大值.
若有一组数据:  ,其中整数
,其中整数  是这组数据的中位数,则这组数据的平均数不可能是( )
是这组数据的中位数,则这组数据的平均数不可能是( )
 ,其中整数
,其中整数  是这组数据的中位数,则这组数据的平均数不可能是( )
是这组数据的中位数,则这组数据的平均数不可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知反比例函数  的图象与直线
的图象与直线  相交于点
相交于点  ,
,  .
.
 的图象与直线
的图象与直线  相交于点
相交于点  ,
,  .
. 
-
(1) 求出直线
 的表达式;
的表达式;
-
(2) 在x轴上有一点
 使得
使得  的面积为18,求出点P的坐标.
的面积为18,求出点P的坐标.
用总长为  的篱笆围成矩形场地,矩形面积
的篱笆围成矩形场地,矩形面积  随矩形一边长
随矩形一边长  的变化而变化.
的变化而变化.
 的篱笆围成矩形场地,矩形面积
的篱笆围成矩形场地,矩形面积  随矩形一边长
随矩形一边长  的变化而变化.
的变化而变化.
-
(1) 当矩形边长
 为多少米时,矩形面积为
为多少米时,矩形面积为  ;
;
-
(2) 求出
 关于
关于  的函数关系式,并直接写出当
的函数关系式,并直接写出当  为何值时,场地的面积
为何值时,场地的面积  最大.
最大.
一个菱形两条对角线长的和是 , 面积是
, 面积是 . 求菱形的周长.
. 求菱形的周长.
 , 面积是
, 面积是 . 求菱形的周长.
. 求菱形的周长.
一个数的平方根和它的立方根相等,则这个数是( )
A . 1
B . 0
C . 1或0
D . 1或0或-1
下列运算正确的是 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一次函数y=-x+1的图象不经过的象限是( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
如果单项式﹣3x2ayb+1与  是同类项,那么这两个单项式的积是.
是同类项,那么这两个单项式的积是.
 是同类项,那么这两个单项式的积是.
是同类项,那么这两个单项式的积是.
某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
|
星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
|
增减 |
-5 |
+7 |
-3 |
+4 |
+10 |
-9 |
-25 |
-
(1) 本周星期六生产多少辆摩托车?
-
(2) 本周总产量与计划产量相比,是增加了还是减少了?为什么?
-
(3) 产量最多的那天比产量最少的那天多生产多少辆?
如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.当AC=4,BC=3时,则阴影部分的面积为( )

A . 6
B .  C .
C .  D . 12
D . 12
 C .
C .  D . 12
D . 12
已知:如图,BD是△ABC的角平分线,点E、F分别在AB、BC上,且ED//BC,EF//AC.

-
(1) 求证:BE=DE;
-
(2) 当AB=AC时,试说明四边形EFCD为菱形.
如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x﹣15|+  =0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=
=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD= 
 =0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=
=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD= 

-
(1) 求点B的坐标;
-
(2) 求直线BN的解析式;
-
(3) 将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
如图,该图是一个正方体的展开图,把展开图折叠成正方体后,有“少”字一面的相对面上的字是.

如图,半径为2的⊙O在第一象限与直线y=x交于点A,反比例函数y=  (k>0)的图象过点A,则k=
(k>0)的图象过点A,则k=
 (k>0)的图象过点A,则k=
(k>0)的图象过点A,则k= 
某中学九(1)班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.训练后篮球定时定点投篮测试进球数统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 ;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%,参加训练之前的人均进球数为 .

请你用学习“一次函数”时积累的经验和方法研究函数  的图象和性质,并解决问题.
的图象和性质,并解决问题.
 的图象和性质,并解决问题.
的图象和性质,并解决问题. 
-
(1) 完成下列步骤,画出函数
 的图象;
的图象; ①列表、填空;
x


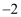

0
1
2
3

y

3
1
1
2
3

②描点:
③连线
-
(2) 观察图象,当x时,y随x的增大而增大;
-
(3) 结合图象,不等式
 的解集为.
的解集为.
已知线段 AB=16 cm ,直线 AB 上有一点 C ,且 BC=10 cm,M 是线段 AC 的中点,则 AM 的长为 ________ cm.
要设计一幅长15㎝, 宽10㎝的长方形图案, 其中有一横一竖两个彩条, 横竖彩条![]() 宽度比为3 :2, 如果要使彩条所占面积为原长方形面积的
宽度比为3 :2, 如果要使彩条所占面积为原长方形面积的![]() , 求每个彩条的宽度.
, 求每个彩条的宽度.
 |
最近更新
- 如图为两个点电荷在真空中所产生电场的电场线(方向未标出).图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为
- PM2.5是指大气中直径小于或等于2.5微米的可吸入颗粒物。下列做法不会改变PM2.5检测结果的是( ) A.海
- 1880年,薛福成写道:“中国立约之初,有视若寻常而贻害于无穷者,大要有二:一则曰,一国获利各国均沾也。……一则曰,洋人
- -- Goodbye, Peter, remember me to your parents. -- __
- 11.下列句子表达得体的一项是( ) A. 日前身份证不慎遗失,幸亏您能够及时送回,实在感激不尽。明天我将于百忙
- 已知反应:( ) ①2C(s)+O2(g)=2CO(g)△H=-221kJ/mol ②H+(aq)+OH-(aq)=
- 现有两个非常大的某昆虫种群,个体间随机交配,没有迁入和迁出,无突变,自然选择对A和a基因控制的形状没有作用.种群1的A基
- 1......
- 一些政府官员在煤矿投资入股而形成“官煤勾结”,庇护一些矿主从事非法生产,是近年来造成煤炭生产安全事故频发的重要原因之一。
- —What should we do for the disabledchildren in the Children'
- 下列各句中,括号中成语使用恰当的一句是( ) A.小镇的马路上,行人车马,(比肩接踵),络绎不绝。 B.这几年短跑
- 有“虫眼”的水果农药含量少。( )
- 一个带电粒子沿垂直于磁场的方向射入该匀强磁场,粒子的后段轨迹如图2-6所示,轨迹上的每一小段都可以近似看成圆弧.由于带电
- 已知复数(为虚数单位),则在复平面内对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第
- 同学们在学习酸碱的化学性质时构建了如右图知识网络,A、B、C、D是不同类别的无机化合物,“—”表示物质在一定条件下可以发
- 哲学上的“两个对子”是 ①可知论和不可知论 ②一元论和二元论③唯物主义和唯心主义
- 如图是小明同学研究串联电路中电流、电压特点的实物连接图,当开关闭合时,灯L1不亮,灯L2亮,电流表的指针明显偏转,电压表
- 基础知识积累与运用:(26分) 1、潮平两岸阔,_________________。(1分) 2、明月别
- 如图,已知直线∥∥∥,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为
- 8、生物体生命活动的主要承担者、遗传信息的携带者、生命活动的主要能源物质依次是( ) A.核酸、蛋白质、



