解三角形的实际应用 知识点题库
在 中,
中, 则使
则使 有两解的x的范围是( )
有两解的x的范围是( )
 中,
中, 则使
则使 有两解的x的范围是( )
有两解的x的范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知在等边△ABC中,AB=3,O为中心,过O的直线与△ABC的边分别交于点M、N,则  +
+  的最大值是( )
的最大值是( )
 +
+  的最大值是( )
的最大值是( )
A .  B . 2
C .
B . 2
C .  D .
D . 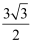
 B . 2
C .
B . 2
C .  D .
D . 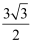
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.

-
(1) 若a=1.5,问:观察者离墙多远时,视角θ最大?
-
(2) 若tanθ=
 ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
我舰在敌岛A处南偏西50°的B处,且A,B距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行.若我舰要用2小时追上敌舰,则其速度大小为海里/小时.
南沙群岛自古以来都是中国领土,南沙海域有A、B两个岛礁相距100海里,从A岛礁望C岛礁和B岛礁成60°的视角,从B岛礁望C岛礁和A岛礁成75°的视角,我国兰州号军舰航在A岛礁处时候B岛礁处指挥部的命令,前往C岛礁处驱赶某国入侵军舰,则我军舰此时离C岛礁距离是( )
A . 100(  +1)海里
B . 50(
+1)海里
B . 50(  +1)海里
C . 50
+1)海里
C . 50  海里
D . 50
海里
D . 50  海里
海里
 +1)海里
B . 50(
+1)海里
B . 50(  +1)海里
C . 50
+1)海里
C . 50  海里
D . 50
海里
D . 50  海里
海里
如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8  n mile.此船的航速是 n mile/h.
n mile.此船的航速是 n mile/h.
 n mile.此船的航速是 n mile/h.
n mile.此船的航速是 n mile/h. 
海滨某城市A附近海面上有一台风,在城市A测得该台风中心位于方位角150°、距离400km的海面P处,并正以70km/h的速度沿北偏西60°的方向移动,如果台风侵袭的范围是半径为250km的圆形区域.
-
(1) 几小时后该城市开始受到台风侵袭?
-
(2) 该台风将持续影响该城市多长时间?
(参考数据:
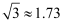 )
)
一艘海轮从A处出发,以40海里/时的速度沿东偏南50°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,求B,C两点间的距离.
如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5  km.
km.
 km.
km. 
-
(1) 求居民区A与C的距离;
-
(2) 现要经过点O铺设一条总光缆直线EF(E在直线OA的上方),并从A,B,C分别铺设三条最短分光缆连接到总光缆EF.假设铺设每条分光缆的费用与其长度的平方成正比,比例系数为m(m为常数).设∠AOE=θ(0≤θ<π),铺设三条分光缆的总费用为w(元).
①求w关于θ的函数表达式;
②求w的最小值及此时tanθ的值.
如图所示,长为  的木棒
的木棒  斜靠在石堤旁,木棒的一端
斜靠在石堤旁,木棒的一端  在离堤足
在离堤足  处
处  的地面上,另一端
的地面上,另一端  在离堤足
在离堤足  处
处  的石堤上,石堤的倾斜角为
的石堤上,石堤的倾斜角为  ,则坡度值
,则坡度值  等于 ( )
等于 ( )
 的木棒
的木棒  斜靠在石堤旁,木棒的一端
斜靠在石堤旁,木棒的一端  在离堤足
在离堤足  处
处  的地面上,另一端
的地面上,另一端  在离堤足
在离堤足  处
处  的石堤上,石堤的倾斜角为
的石堤上,石堤的倾斜角为  ,则坡度值
,则坡度值  等于 ( )
等于 ( )
A .  B .
B . 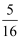 C .
C .  D .
D . 
 B .
B . 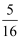 C .
C .  D .
D . 
 的三个内角
的三个内角  所对的边分别为
所对的边分别为  ,且满足
,且满足  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D .  或
或 
 B .
B .  C .
C .  D .
D .  或
或 
如图所示,一辆汽车从  市出发沿海岸一条直公路以
市出发沿海岸一条直公路以  的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在  市南偏东30°方向距
市南偏东30°方向距  市
市  的海上
的海上  处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以  的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在  市南偏东30°方向距
市南偏东30°方向距  市
市  的海上
的海上  处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
两灯塔A,B与海洋观察站C的距离都等于a(km),灯塔A在C北偏东30°,B在C南偏东60°,则A,B之间相距( )
A .  a(km)
B .
a(km)
B . 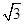 a(km)
C . a(km)
D . 2a(km)
a(km)
C . a(km)
D . 2a(km)
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得  .已知山高BC=100m,则山高MN=m.
.已知山高BC=100m,则山高MN=m.
 .已知山高BC=100m,则山高MN=m.
.已知山高BC=100m,则山高MN=m. 
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度  的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为
的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为  和
和  ,第一排和最后一排的距离为
,第一排和最后一排的距离为  米(如图所示),旗杆底部与第一排在同一个水平面上.若国歌长度约为50秒,要使国歌结束时国旗刚好升到旗杆顶部,升旗手升旗的速度应为( )(米/秒)
米(如图所示),旗杆底部与第一排在同一个水平面上.若国歌长度约为50秒,要使国歌结束时国旗刚好升到旗杆顶部,升旗手升旗的速度应为( )(米/秒)
 的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为
的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为  和
和  ,第一排和最后一排的距离为
,第一排和最后一排的距离为  米(如图所示),旗杆底部与第一排在同一个水平面上.若国歌长度约为50秒,要使国歌结束时国旗刚好升到旗杆顶部,升旗手升旗的速度应为( )(米/秒)
米(如图所示),旗杆底部与第一排在同一个水平面上.若国歌长度约为50秒,要使国歌结束时国旗刚好升到旗杆顶部,升旗手升旗的速度应为( )(米/秒) 
A . 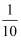 B .
B . 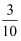 C .
C .  D .
D . 
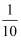 B .
B . 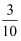 C .
C .  D .
D . 
目前,中国已经建成全球最大的5G网络,无论是大山深处还是广袤平原,处处都能见到5G基站的身影.如图,某同学在一条水平公路上观测对面山项上的一座5G基站AB,已知基站高  ,该同学眼高1.5m(眼睛到地面的距离),该同学在初始位置C处(眼睛所在位置)测得基站底部B的仰角为37°,测得基站顶端A的仰角为45°.
,该同学眼高1.5m(眼睛到地面的距离),该同学在初始位置C处(眼睛所在位置)测得基站底部B的仰角为37°,测得基站顶端A的仰角为45°.
 ,该同学眼高1.5m(眼睛到地面的距离),该同学在初始位置C处(眼睛所在位置)测得基站底部B的仰角为37°,测得基站顶端A的仰角为45°.
,该同学眼高1.5m(眼睛到地面的距离),该同学在初始位置C处(眼睛所在位置)测得基站底部B的仰角为37°,测得基站顶端A的仰角为45°. 
参考数据:  ,
,  ,
,  ,
,  .
.
-
(1) 求出山高BE(结果保留整数);
-
(2) 如图,当该同学面向基站AB前行时(保持在同一铅垂面内),记该同学所在位置M处(眼睛所在位置)到基站AB所在直线的距离
 ,且记在M处观测基站底部B的仰角为
,且记在M处观测基站底部B的仰角为  ,观测基站顶端A的仰角为
,观测基站顶端A的仰角为  .试问当
.试问当  多大时,观测基站的视角
多大时,观测基站的视角  最大?
最大?
汽车最小转弯半径是指当转向盘转到极限位置,汽车以最低稳定车速转向行驶时,外侧转向轮的中心平面在支承平面上滚过的轨迹圆半径.如图中的BC即是.已知某车在低速前进时,图中A处的轮胎行进方向与AC垂直,B处的轮胎前进方向与BC垂直,轴距AB为2.92米,方向盘转到极限时,轮子方向偏了30°,则该车的最小转弯半径BC为米.

旅游区的玻璃栈道、玻璃桥、玻璃景观台等近年来热搜不断,因其惊险刺激的体验备受追捧.某景区顺应趋势,为扩大营收,准备在如图所示的 山峰和
山峰和 山峰间建一座空中玻璃观景桥.已知两座山峰的高度都是
山峰间建一座空中玻璃观景桥.已知两座山峰的高度都是 , 从
, 从 点测得
点测得 点的仰角
点的仰角 ,
,  点的仰角
点的仰角 以及
以及 , 则两座山峰之间的距离
, 则两座山峰之间的距离 ( )
( )
 山峰和
山峰和 山峰间建一座空中玻璃观景桥.已知两座山峰的高度都是
山峰间建一座空中玻璃观景桥.已知两座山峰的高度都是 , 从
, 从 点测得
点测得 点的仰角
点的仰角 ,
,  点的仰角
点的仰角 以及
以及 , 则两座山峰之间的距离
, 则两座山峰之间的距离 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,经过村庄B有两条夹角为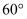 的公路BA和BC,根据规划拟在两条公路之间的区域内建一工厂F,分别在两条公路边上建两个仓库D和E(异于村庄B),设计要求
的公路BA和BC,根据规划拟在两条公路之间的区域内建一工厂F,分别在两条公路边上建两个仓库D和E(异于村庄B),设计要求 (单位:千米).
(单位:千米).
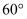 的公路BA和BC,根据规划拟在两条公路之间的区域内建一工厂F,分别在两条公路边上建两个仓库D和E(异于村庄B),设计要求
的公路BA和BC,根据规划拟在两条公路之间的区域内建一工厂F,分别在两条公路边上建两个仓库D和E(异于村庄B),设计要求 (单位:千米).
(单位:千米).
-
(1) 若
 , 求
, 求 的值(保留根号);
的值(保留根号);
-
(2) 若设
 , 当
, 当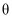 为何值时,工厂产生的噪音对村庄B的居民影响最小(即工厂F与村庄B的距离最远),并求其最远距离.(精确到0.1,取
为何值时,工厂产生的噪音对村庄B的居民影响最小(即工厂F与村庄B的距离最远),并求其最远距离.(精确到0.1,取 )
)
如图,一同学利用所学习的解三角形知识想测量河对岸的塔高 时,他选取了塔底B在同一水平面内的两个测量基点C与D.
时,他选取了塔底B在同一水平面内的两个测量基点C与D. ,
,  ,
,  , 在点C处塔顶A的仰角为60°,则塔高为( )
, 在点C处塔顶A的仰角为60°,则塔高为( )
 时,他选取了塔底B在同一水平面内的两个测量基点C与D.
时,他选取了塔底B在同一水平面内的两个测量基点C与D. ,
,  ,
,  , 在点C处塔顶A的仰角为60°,则塔高为( )
, 在点C处塔顶A的仰角为60°,则塔高为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- “频闪摄影”是研究物体运动时常用的一种实
- 观察下列等式: ①3﹣2=(﹣1)2, ②5﹣2=
- 设椭圆的左焦点为F, 离心率为, 过点F且与x轴
- 下列有关物理学史的说法中正确的是 A. 伽利
- 下列溶液分别加热蒸干,可以得到该物质晶体
- 民主革命时期的标语宣传了党的政策,播撒了
- 函数y=2x2+4x+1①;y=2x2- 4x+1②的图象的位置关
- 词形变换;用括号内所给单词的适当形式填空
- 如图12-2-12所示为一列简谐波某时刻的波形图
- 下列说法中,正确的是D A.BF3分子中没有原子
- 用0.1 mol·L-1 NaOH溶液滴定100 mL 0.1 mol·L-1盐酸时
- 中国网2014年3月5日讯:李克强说今年将继续实
- 指出下列句子翻译的错误及原因。 (1)是女
- 如图,在△ABC中,D是BC边上的点(不与B,C重
- 如图5所示,“套圈”出手后,从a点到c点的过
- (2009年合肥市高三第一次教学质量检测)When you
- 下列化合物的一氯代物的数目排列顺序正确的
- 如图所示,在地面A点斜向上抛出一个小球,
- 目前我国已经建成比较完备的公路网,它既是
- 下列实验操作中,正确的是( ) A. B. C



