解直角三角形的应用﹣仰角俯角问题 知识点题库
如图,一次函数y=kx+b的图象与反比例函数y=﹣ 的图象交于A(﹣1,m)、B(n,﹣1)两点。
的图象交于A(﹣1,m)、B(n,﹣1)两点。

-
(1) 求一次函数的解析式;
-
(2) 求
 的面积。
的面积。
小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)(参考数据:sin37°
 ,tan37°
,tan37°
 ,sin48°
,sin48°
 ,tan48°
,tan48°
 )
)

如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8  m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的高度是( )m.
m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的高度是( )m.
 m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的高度是( )m.
m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的高度是( )m. 
A . 8  +24
B . 8
+24
B . 8  +8
C . 24+8
+8
C . 24+8  D . 8+8
D . 8+8 
 +24
B . 8
+24
B . 8  +8
C . 24+8
+8
C . 24+8  D . 8+8
D . 8+8 
某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ 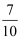 ,tan48°≈
,tan48°≈ 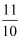 ,sin64°≈
,sin64°≈ 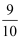 ,tan64°≈2)
,tan64°≈2)

如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(  =1.732,结果精确到0.1米)
=1.732,结果精确到0.1米)
 =1.732,结果精确到0.1米)
=1.732,结果精确到0.1米)
图①为平地上一幢建筑物与铁塔图,图②为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=20m,在A点测得D点的俯角为45°,测得C点的仰角为58°.求铁塔CD的高度.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)

随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为 开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测 量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°,测得瀑布底端 B 点的俯角是 10°,AB与水平面垂直.又在瀑布下的水平面测得 CG=27m, GF=17.6m(注:C、G、F 三点在同一直线上,CF⊥AB 于点 F).斜坡 CD=20m, 坡角∠ECD=40°.求瀑布 AB 的高度.(参考数据:  ≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
 ≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
如图,小明所在教学楼的每层高度为3.5m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1m.

-
(1) AB=m;
-
(2) 求旗杆MN的高度.(结果保留两位小数)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为m(结果保留根号).

如图,某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=60m,山坡的坡比为1:2.

-
(1) 求该建筑物的高度(即AB的长,结果保留根号);
-
(2) 求此人所在位置点P的铅直高度(即PD的长,结果保留根号).
如图,长沙九龙仓国际金融中心主楼  高达
高达  ,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼
,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼  高
高  ,为了测量高楼
,为了测量高楼  上发射塔
上发射塔 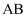 的高度,在楼
的高度,在楼 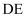 底端
底端  点测得
点测得  的仰角为α,
的仰角为α,  ,在顶端E测得A的仰角为
,在顶端E测得A的仰角为  ,求发射塔
,求发射塔 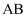 的高度.
的高度.
 高达
高达  ,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼
,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼 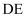 高
高  ,为了测量高楼
,为了测量高楼  上发射塔
上发射塔 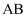 的高度,在楼
的高度,在楼 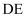 底端
底端  点测得
点测得  的仰角为α,
的仰角为α,  ,在顶端E测得A的仰角为
,在顶端E测得A的仰角为  ,求发射塔
,求发射塔 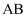 的高度.
的高度. 
如图所示,王林到某景区参观大佛(AB),他在E点直立测得大佛顶端的仰角为 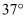 ,当其再次前行6. 43米在G点测得大佛顶端的仰角为
,当其再次前行6. 43米在G点测得大佛顶端的仰角为  ,若已知大佛(AB)的高度为21米,请你依据数据计算王林同学的身高为多少米?(结果精确到0. 1米)
,若已知大佛(AB)的高度为21米,请你依据数据计算王林同学的身高为多少米?(结果精确到0. 1米)
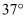 ,当其再次前行6. 43米在G点测得大佛顶端的仰角为
,当其再次前行6. 43米在G点测得大佛顶端的仰角为  ,若已知大佛(AB)的高度为21米,请你依据数据计算王林同学的身高为多少米?(结果精确到0. 1米)
,若已知大佛(AB)的高度为21米,请你依据数据计算王林同学的身高为多少米?(结果精确到0. 1米) (参考数据:  )
)


如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,  =1.73,精确到0.1m)
=1.73,精确到0.1m)
 =1.73,精确到0.1m)
=1.73,精确到0.1m) 
如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( )

A . 60m
B . 40  m
C . 30
m
C . 30  m
D . 60
m
D . 60  m
m
 m
C . 30
m
C . 30  m
D . 60
m
D . 60  m
m
如图,某建筑物  顶部有一旗杆
顶部有一旗杆  ,且点A , B , C在同一条直线上,小红在D处观测旗杆顶部A的仰角为
,且点A , B , C在同一条直线上,小红在D处观测旗杆顶部A的仰角为  ,观测旗杆底部B的仰角为
,观测旗杆底部B的仰角为  ,已知点D到地面的距离
,已知点D到地面的距离  为
为  ,
,  ,求旗杆
,求旗杆  的高度和建筑物
的高度和建筑物  的高度(结果保留小数点后一位).参考数据:
的高度(结果保留小数点后一位).参考数据:  .
.
 顶部有一旗杆
顶部有一旗杆  ,且点A , B , C在同一条直线上,小红在D处观测旗杆顶部A的仰角为
,且点A , B , C在同一条直线上,小红在D处观测旗杆顶部A的仰角为  ,观测旗杆底部B的仰角为
,观测旗杆底部B的仰角为  ,已知点D到地面的距离
,已知点D到地面的距离  为
为  ,
,  ,求旗杆
,求旗杆  的高度和建筑物
的高度和建筑物  的高度(结果保留小数点后一位).参考数据:
的高度(结果保留小数点后一位).参考数据:  .
. 
如图,小明所在的兴趣小组站在广场的  ,
,  处,用一定高度的测角仪分别于
处,用一定高度的测角仪分别于  ,
,  两处测得雕像顶部
两处测得雕像顶部  的仰角分别为
的仰角分别为  ,
,  .已知
.已知  ,
,  两点的距离为
两点的距离为  ,雕像下的基座高度
,雕像下的基座高度  为
为  ,求雕像
,求雕像  的高度.(精确到
的高度.(精确到  ,
,  )
)
 ,
,  处,用一定高度的测角仪分别于
处,用一定高度的测角仪分别于  ,
,  两处测得雕像顶部
两处测得雕像顶部  的仰角分别为
的仰角分别为  ,
,  .已知
.已知  ,
,  两点的距离为
两点的距离为  ,雕像下的基座高度
,雕像下的基座高度  为
为  ,求雕像
,求雕像  的高度.(精确到
的高度.(精确到  ,
,  )
) 
避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼  顶部避雷针
顶部避雷针  的长度(
的长度(  ,
,  ,
,  三点共线),在水平地面
三点共线),在水平地面  点测得
点测得  ,
,  ,
,  点与大楼底部
点与大楼底部  点的距离
点的距离  ,求避雷针
,求避雷针  的长度.(结果精确到
的长度.(结果精确到  .参考数据:
.参考数据:  ,
,  ,
,  ,
, 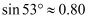 ,
,  ,
,  )
)
 顶部避雷针
顶部避雷针  的长度(
的长度(  ,
,  ,
,  三点共线),在水平地面
三点共线),在水平地面  点测得
点测得  ,
,  ,
,  点与大楼底部
点与大楼底部  点的距离
点的距离  ,求避雷针
,求避雷针  的长度.(结果精确到
的长度.(结果精确到  .参考数据:
.参考数据:  ,
,  ,
,  ,
, 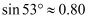 ,
,  ,
,  )
) 
2020年12月8日,中国、尼泊尔两国向全世界正式宣布,珠穆朗玛峰的最新高程为8848.86米.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,则山高BC是多少米.

如图,某大楼(DE)的顶部树有一块广告牌CD,实践小组在斜坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°.已知斜坡的坡比为 ,
,  米,
米, 米.求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
米.求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ,
,  )
)
 ,
,  米,
米, 米.求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
米.求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ,
,  )
)
镇北台位于陕西省榆林城北4公里之红山顶上.据险临下,控南北之咽喉,如巨锁扼边关要隘,为古长城沿线现存最大的要塞之一.某“综合与实践”小组开展了测量镇北台高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量、如图,他们先在镇北台底部所在的平地上,放置一个平面镜E,甲同学后退到点D时,刚好从镜子中看到镇北台的顶端点A的像,测得 , 甲同学的眼睛到地面的距离
, 甲同学的眼睛到地面的距离 为1.5m;然后,利用测角仪在点F处测得镇北台的顶端点A的仰角为45°,测角仪的高
为1.5m;然后,利用测角仪在点F处测得镇北台的顶端点A的仰角为45°,测角仪的高 ,
,  .已知
.已知 ,
,  ,
,  , 点B、E、D、F在一条直线上,请你求出镇北台的高度
, 点B、E、D、F在一条直线上,请你求出镇北台的高度 .
.
 , 甲同学的眼睛到地面的距离
, 甲同学的眼睛到地面的距离 为1.5m;然后,利用测角仪在点F处测得镇北台的顶端点A的仰角为45°,测角仪的高
为1.5m;然后,利用测角仪在点F处测得镇北台的顶端点A的仰角为45°,测角仪的高 ,
,  .已知
.已知 ,
,  ,
,  , 点B、E、D、F在一条直线上,请你求出镇北台的高度
, 点B、E、D、F在一条直线上,请你求出镇北台的高度 .
.
最近更新
- 解不等式组,并把解集在数轴上表示出来.
- 如图所示,若电解5min时,测得铜电极的质量
- 某列从杭州到温州的火车,包括起始和终点在
- 下列各组词语中,加点字的读音都正确的一项
- Jack had traveled six miles across the Channel ______ his en
- With all factors ________,we think this program may be bette
- 下表是2014年前三季度我国三大产业发展情况
- 如下图是四位同学设计的用伏安法测电阻R的
- In June, 2007, a group of students from eight high schools i
- 吉安读水 江西的南部,有一条美丽的水叫章
- (1)已知x<,求函数y=4x-2+的最大值;(2)已知x>0,
- 关于乙炔分子结构的描述错误的是( ) A.乙炔
- 下列离子方程式书写正确的是 A.钠和冷水反
- 下列属于同一结构层次的是( ) A.番茄表皮与
- 心脏内血流方向是( )A. 心房→心室→动
- 某同学做物质在氧气中燃烧的实验,方法如图
- 第二节:完形填空(共20小题;每小题1.5分,
- 截至9月底,2010年全国已有30个省份调整了最
- 阅读下面两首唐诗,然后回答问题。 江亭夜
- 要解决世界和平与发展问题的主要障碍问题,



