解直角三角形的应用﹣仰角俯角问题 知识点题库
在寻找马航MH370航班过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=1500米,  =
= , 则飞机距疑似目标B的水平距离BC为( )
, 则飞机距疑似目标B的水平距离BC为( )
 =
= , 则飞机距疑似目标B的水平距离BC为( )
, 则飞机距疑似目标B的水平距离BC为( )
A . 2400 米
B . 2400
米
B . 2400 米
C . 2500
米
C . 2500 米
D . 2500
米
D . 2500 米
米
 米
B . 2400
米
B . 2400 米
C . 2500
米
C . 2500 米
D . 2500
米
D . 2500 米
米
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)

如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为米.(精确到1米,参考数据:  ≈1.73)
≈1.73)

如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:  ≈1.73)
≈1.73)

如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.

-
(1) 用α和β的三角函数表示CE;
-
(2) 当α=30°、β=60°时,求EF(结果精确到1m).
(参考数据:
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为米.

吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:  ≈1.73,结果保留整数)
≈1.73,结果保留整数)
 ≈1.73,结果保留整数)
≈1.73,结果保留整数)
如图,在教学楼距地面8米高的窗口中C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°.升旗时,国旗上端悬挂在距地面2米处.若国旗随国歌声冉冉升起,并在国歌播放40秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上,求旗杆AB的高度.(结果精确到0.1m,参考数据:  ≈1.41,
≈1.41,  =1.73)
=1.73)
 ≈1.41,
≈1.41,  =1.73)
=1.73) 
大雁塔南广场玄奘铜像是为纪念唐代高僧玄奘而设计.在一次课外活动中,甲、乙两位同学测量玄奘铜像的高度他们分别在A,B两处用高度为1.8m的测角仪测得铜像顶部C的仰角分别为30°,60°,两人间的水平距离AB为10m,求玄奘铜像的高度CF.(结果保留根号)

如图,为加快5G网络建设,某通信公司在一个坡度i=1:2.4的山坡AB上建了一座信号塔CD,信号塔底端C到山脚A的距离AC=13米,在距山脚A水平距离18米的E处,有一高度为10米的建筑物EF,在建筑物顶端F处测得信号塔顶端D的仰角为37°(信号塔及山坡的剖面和建筑物的剖面在同一平面上),则信号塔CD的高度约是( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A . 22.5米
B . 27.5米
C . 32.5米
D . 45.0米
“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔  的高度,他从点D处的观景塔出来走到点A处.沿着斜坡AB从A点走了8米到达B点,此时回望观景塔,更显气势宏伟.在B点观察到观景塔顶端的仰角为
的高度,他从点D处的观景塔出来走到点A处.沿着斜坡AB从A点走了8米到达B点,此时回望观景塔,更显气势宏伟.在B点观察到观景塔顶端的仰角为  且
且  ,再往前走到C处,观察到观景塔顶端的仰角
,再往前走到C处,观察到观景塔顶端的仰角 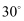 ,测得BC之间的水平距离
,测得BC之间的水平距离  米,则观景塔的高度DE约为( ) 米. (
米,则观景塔的高度DE约为( ) 米. (  )
)
 的高度,他从点D处的观景塔出来走到点A处.沿着斜坡AB从A点走了8米到达B点,此时回望观景塔,更显气势宏伟.在B点观察到观景塔顶端的仰角为
的高度,他从点D处的观景塔出来走到点A处.沿着斜坡AB从A点走了8米到达B点,此时回望观景塔,更显气势宏伟.在B点观察到观景塔顶端的仰角为  且
且  ,再往前走到C处,观察到观景塔顶端的仰角
,再往前走到C处,观察到观景塔顶端的仰角 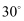 ,测得BC之间的水平距离
,测得BC之间的水平距离  米,则观景塔的高度DE约为( ) 米. (
米,则观景塔的高度DE约为( ) 米. (  )
) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者,在消防车上点A处测得点B和点C的仰角分别为45和65°,点A距地面2.5米,点B距地面10.5米,为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?
(结果保留整数,参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,  ≈1.4)
≈1.4)

如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为  ,从A处看风筝的仰角为
,从A处看风筝的仰角为  ,小明的父母从C处看风筝的仰角为
,小明的父母从C处看风筝的仰角为 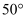 .
.
 ,从A处看风筝的仰角为
,从A处看风筝的仰角为  ,小明的父母从C处看风筝的仰角为
,小明的父母从C处看风筝的仰角为 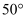 .
. 
-
(1) 风筝离地面多少m?
-
(2) AC相距多少m?(结果保留小数点后一位,参考数据:
 ,
,  ,
,  ,
,  ,
,  ,
,  )
)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B、C、E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B、C两点间的距离(结果精确到0.1m).(参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732) 
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°,若亮亮身高1.70米,则无人机距离地面的高度约为米.(结果保留根号)

镇淮楼巍峨高大,古色古香,是淮安古老而文明的象征之一.如图,AB为镇淮楼楼身,已知AB⊥BC,CD⊥BC,BC=22米,CD=1.7米,从D点看楼顶A的仰角为37.5°.请你根据题中提供的相关信息,求出镇淮楼的高AB的长度.(结果精确到0.1米,参考数据:sin37.5°≈0.609,cos37.5°≈0.793,tan37.5°≈0.767)

如图,教学楼AB与旗杆CD的距离BC=12m,O在AB上,且OB= 1.5m,在某次数学活动课中,甲小组在A测得旗杆顶部D的俯角为30°,同时乙小组从0处测得旗杆顶部D的仰角为38.7°,求教学楼AB的高度(精确到0.1m),(参考数据::sin38.7°≈0.63,cos38.7≈0.78,tan38.7°=0.80, =1.73)
=1.73)
 =1.73)
=1.73)
如图,岸边堤坝和湖中分别伫立着甲、乙两座电线塔,甲塔底  和堤坝
和堤坝  段均与水平面
段均与水平面  平行,
平行,  为
为  中点,
中点,  米,
米,  米.某时刻甲塔顶
米.某时刻甲塔顶 
 影子恰好落在斜坡底端
影子恰好落在斜坡底端  处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点
处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点  处,发现点
处,发现点  ,
,  ,
,  三点共线,并在
三点共线,并在  处测得甲塔底
处测得甲塔底  和乙塔顶
和乙塔顶  的仰角均为
的仰角均为  ,则塔高
,则塔高  的长为米;若小章继续向右行驶10米至点
的长为米;若小章继续向右行驶10米至点  ,且在
,且在  处测得甲、乙两塔顶
处测得甲、乙两塔顶  ,
,  的仰角均为
的仰角均为  .若点
.若点  ,
,  ,
,  ,
,  在同一水平线上,
在同一水平线上,  ,则甲、乙两塔顶
,则甲、乙两塔顶  ,
,  的距离为米.(参考数据:
的距离为米.(参考数据:  ,
,  ,
,  ,
,  )
)
 和堤坝
和堤坝  段均与水平面
段均与水平面  平行,
平行,  为
为  中点,
中点,  米,
米,  米.某时刻甲塔顶
米.某时刻甲塔顶 
 处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点
处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点  处,发现点
处,发现点  ,
,  ,
,  三点共线,并在
三点共线,并在  处测得甲塔底
处测得甲塔底  和乙塔顶
和乙塔顶  的仰角均为
的仰角均为  ,则塔高
,则塔高  的长为米;若小章继续向右行驶10米至点
的长为米;若小章继续向右行驶10米至点  ,且在
,且在  处测得甲、乙两塔顶
处测得甲、乙两塔顶  ,
,  的仰角均为
的仰角均为  .若点
.若点  ,
,  ,
,  ,
,  在同一水平线上,
在同一水平线上,  ,则甲、乙两塔顶
,则甲、乙两塔顶  ,
,  的距离为米.(参考数据:
的距离为米.(参考数据:  ,
,  ,
,  ,
,  )
)

最近更新
- 已知甲为恒温、恒压容器,乙为恒温、恒容容
- 第二次世界大战期间,中国参与签署的反法西
- He is old enough to travel ____. After all, he is alrea
- 下列各句中,没有错别字的一项是 (
- 下列各选项中两种粒子所含电子数不相等的是
- 朝鲜于2012年12月12日发射了光明星3号卫星。对
- 要了解近几天的天气情况,主要渠道有(
- 二面角的大小是60°,线段.,与所成的角为30°
- 图是一列简谐横波在某时刻的波形图,已知图
- 《什么是民主》指出:“公元前五、六世纪
- 2013年3月31日,由清华大学和美国健康影响研
- 硫酸铜晶体常用作农业和渔业的杀虫剂、杀菌
- 在复平面内,复数对应的点位于( )
- 用纯种高茎黄子叶(DDYY)和纯种矮茎绿子叶(ddyy)
- 关于地质构造和构造地貌的叙述,错误的是(
- 明清时期商业继续繁荣,促进了城市的发展。
- 在“DIS描绘电场等势线”的实验中,(1)给
- 读图,以下叙述正确的是 A.在河段C,河谷
- 蝴蝶和家蚕的发育过程为完全变态发育,一般
- 文艺工作者必须虚心向人民群众学习,从人民



