解直角三角形的应用﹣仰角俯角问题 知识点题库
如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数, ≈1.7,
≈1.7, ≈1.4 ).
≈1.4 ).

如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°,1s后,火箭到达B点,此时测得仰角为45.5°,这枚火箭从点A到点B的平均速度是多少?(结果精确到0.01)

这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5  米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )

如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )

 米
C . 15
米
C . 15  米
D . 5
米
D . 5  米
米
 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
-
(1) 求点B距水平面AE的高度BH;
-
(2) 求广告牌CD的高度.




![]()

 )
) 

(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°=1.192)

(参考数据:  ,
,  ,
,  ,
,  )
)


 )始终以
)始终以  的速度在离地面
的速度在离地面  高的上空匀速向右飞行,2号试飞机(看成点
高的上空匀速向右飞行,2号试飞机(看成点  )一直保持在1号机
)一直保持在1号机  的正下方 , 2号机从原点
的正下方 , 2号机从原点  处沿
处沿  仰角爬升,到
仰角爬升,到  高的
高的  处便立刻转为水平飞行,再过
处便立刻转为水平飞行,再过  到达
到达  处开始沿直线
处开始沿直线  降落,要求
降落,要求  后到达
后到达  处.
处. 
-
(1) 求
 的
的  关于
关于  的函数解析式,并直接写出2号机的爬升速度;
的函数解析式,并直接写出2号机的爬升速度;
-
(2) 求
 的
的  关于
关于  的函数解析式,并预计2号机着陆点的坐标;
的函数解析式,并预计2号机着陆点的坐标;
-
(3) 通过计算说明两机距离
 不超过
不超过  的时长是多少.
的时长是多少. (注:(1)及(2)中不必写
 的取值范围)
的取值范围)
 )进行测量.因塔底部
)进行测量.因塔底部  无法直接到达,制定了如下的测量方案:先在该塔正前方广场地面
无法直接到达,制定了如下的测量方案:先在该塔正前方广场地面  处测得塔尖
处测得塔尖  的仰角(
的仰角(  )为45°,因广场面积有限,无法再向
)为45°,因广场面积有限,无法再向  点的正后方移动,故操控无人机飞到
点的正后方移动,故操控无人机飞到  点正上方10米的
点正上方10米的  处测得塔尖
处测得塔尖  的仰角为32°,
的仰角为32°,  ,
,  ,
,  ,
,  四点在同一个平面内,求塔高(
四点在同一个平面内,求塔高(  )为多少米.(结果精确到0.1米,参考数据:
)为多少米.(结果精确到0.1米,参考数据:  ,
,  ,
,  )
) 


课题 | 测量公关铜像的高度 | |||
成员 | 组长:×××,组员:×××,×××,××× | |||
工具 | 侧倾器,皮尺等 | |||
设计方案 | 方案一 测量示 意图 |
| 说明:线段 | |
方案二 测量示 意图 |
| 说明:线段 | ||
实施方案 | 方案二的 测量数据 |
|
|
|
|
|
| ||
-
(1) “综合与实践”小组为什么放弃方案一,你认为原因可能是什么?(写出一条即可)
-
(2) 请你根据他们的测量数据计算公关铜像的高度.
(参考数据:
 ,
,  ,
,  )
)
 前点A处垂直升空一无人机巡查小区,当无人机升高到离地面100米的点D处时,以5米每秒的速度沿
前点A处垂直升空一无人机巡查小区,当无人机升高到离地面100米的点D处时,以5米每秒的速度沿 方向飞行,已知点A观察楼顶C的仰角是
方向飞行,已知点A观察楼顶C的仰角是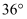 , 问自D点飞行多少秒时无人机刚好离开张明的视线?参考数据:
, 问自D点飞行多少秒时无人机刚好离开张明的视线?参考数据: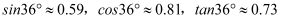

- 阅读材料,完成下列要求。 2016年3月《
- 已知三角形的两边长分别为4,5,它们夹角的余
- 在一不可变容器中发生如下反应:2NO2 2NO + O
- 从首次提出 “建立两岸经济合作机制”
- 依次填入下列各句横线上的词语,恰当的一组
- 影响我国外流河水量变化的主要因素是
- 钢是用量最大、用途最广的合金,下列说法不
- 下图是我国某地区等高线地形图,读图回答。
- 根据拼音写汉字,给加横线的字注音。(2分
- 根据下面的情境,补写小鸟与雄鹰的心理活动
- 阅读下面的材料,根据要求作文。 扁鹊兄弟
- 下面图示中,图甲是反射弧的结构模式图,图
- 已知不重合的直线a,b和平面β. ①若a∥β,b
- 人的神经系统中, 有些神经细胞既能传导兴
- 我国公有制经济是社会主义制度的经济基础。
- 现有八种物质:①熟石灰、②纯碱、③磷矿粉
- 如图所示为氢原子的能级图,现让一束单色光
- 下图中A、B、C、D、E、F、G均为有机化合物。
- 为了研究兴奋在神经元轴突上的传导是单向的
- Many people believe we are heading for environment disaster

 表示侧倾器,
表示侧倾器, 米,点
米,点 在
在 的度数.
的度数.
 表示侧倾器,
表示侧倾器, 的高度为
的高度为 ,
,  在同一平面内.需要测量的数据有
在同一平面内.需要测量的数据有 的距离,倾斜角
的距离,倾斜角 的度数.
的度数.
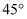
 米
米


