解直角三角形的应用﹣仰角俯角问题 知识点题库
小莉站在离一棵树水平距离为a米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为( )
A .  米
B .
米
B .  米
C .
米
C .  米
D .
米
D .  米
米
 米
B .
米
B .  米
C .
米
C .  米
D .
米
D .  米
米
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).

如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m.
(1)求建筑物BC的高度;
(2)求旗杆AB的高度.
(结果精确到0.1m.参考数据: ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)

一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62米,到达D点,在测得山顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC(结果精确的1米,参考数值:  )
)

如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.

如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:  ≈1.41,
≈1.41,  ≈2.45)
≈2.45)
 ≈1.41,
≈1.41,  ≈2.45)
≈2.45)
如图,在某建筑物AB的顶部点A处观测,测得河对岸C处的俯角为30°,河的这一岸D处的俯角为60°,已知建筑物的高AB等于18米,求河宽CD.(结果保留根号)

乌鞘岭隧道群是连霍国道主干线上隧道最密集、路线最长、海拔最高、地质条件最复杂、施工难度最大的咽喉工程.乌鞘岭特长公路隧道群的全部贯通,将使连霍国道主干线在甘肃境内1608公里路段全部实现高速化,同时也使甘肃河西五市与省会兰州及东南沿海省、市实现全线高速连接.如图,在建设中为确定某隧道AB的长度,测量人员在离地面2700米高度C处的飞机上,测得正前方A、B两点处的俯角分别是60°和30°,求隧道AB的长(结果保留根号)

如图,为了测量旗杆的高度BC,在距旗杆底部B点10米的A处,用高1.5米的测角仪DA测得旗杆顶端C的仰角∠CDE为52°,求旗杆BC的高度.(结果精确到0.1米)【参考数据sin52°=0.79,cos52°=0.62,tan52°=1.28】

如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度.(sin30°=0.50,cos30°≈0.87,tan30°≈0.58)

如图,利用一幢已知高度的楼房CD(楼高为20m),来测量一幢高楼AB的高在DB上选取观测点E、F,从E测得楼房CD和高楼AB的顶部C、A的仰角分别为58°、45°.从F测得C,A的仰角分别为22°,70°.求楼AB的高度(精确到1m)(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75)

在距离大足城区的1.5公里的北山之上,有一处密如峰房的石窟造像点,今被称为北山石窟.北山石窟造像在两宋时期达到鼎盛,逐渐都成了以北山佛湾为中心,环绕营盘坡、佛耳岩,观音坡、多宝塔等多处造像点的大型石窟群.多宝塔,也称为“白塔”“北塔”,于岩石之上,为八角形阁式砖塔,外观可辨十二级,其内有八层楼阁,可沿着塔心内的梯道逐级而上,元且期间,小华和妈妈到大足北山游玩,小华站在坡度为l=1:2的山坡上的B点观看风景,恰好看到对面的多宝培,测得眼睛A看到塔顶C的仰角为30°,接着小华又向下走了10  米,刚好到达坡底E,这时看到塔顶C的仰角为45°,若AB=1.5米,则多宝塔的高度CD约为( )(精确到0.1米,参考数据
米,刚好到达坡底E,这时看到塔顶C的仰角为45°,若AB=1.5米,则多宝塔的高度CD约为( )(精确到0.1米,参考数据  ≈1.732)
≈1.732)
 米,刚好到达坡底E,这时看到塔顶C的仰角为45°,若AB=1.5米,则多宝塔的高度CD约为( )(精确到0.1米,参考数据
米,刚好到达坡底E,这时看到塔顶C的仰角为45°,若AB=1.5米,则多宝塔的高度CD约为( )(精确到0.1米,参考数据  ≈1.732)
≈1.732) 
A . 51.0米
B . 52.5米
C . 27.3米
D . 28.8米
如图,为了测量某风景区内一座古塔AB的高度,小明分别在塔的对面CD楼楼底C、楼顶D处,测得塔顶A的仰角分别为45°和30°,已知楼CD的高为10米,则塔AB的高度为米(结果保留根号)。

如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角∠APQ为15°,山脚B处的俯角∠BPQ为60°,已知该山坡的坡度i(即tan∠ABC)为1:  ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
 ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC. 
-
(1) 求出山坡坡角(∠ABC)的大小;
-
(2) 求A、B两点间的距离(结果精确到0.1米,参考数据:
 ≈1.732).
≈1.732).
鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度  .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为
.如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为  ,无人机沿水平线
,无人机沿水平线 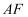 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段
方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段  的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中
的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中  米.
米.
 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为
.如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为  ,无人机沿水平线
,无人机沿水平线 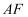 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段
方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段  的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中
的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中  米.
米. 
-
(1) 求无人机的飞行高度
 ;(结果保留根号)
;(结果保留根号)
-
(2) 求河流的宽度
 .(结果精确到1米,参考数据:
.(结果精确到1米,参考数据:  )
)
2020年5月5日,为我国载人空间站工程研制的长征五号运较火箭在海南文昌首飞成功.运载火箭从地面  处发射、当火箭到达点
处发射、当火箭到达点  时,地面
时,地面  处的雷达站测得
处的雷达站测得  米,仰角为
米,仰角为  .3秒后,火箭直线上升到达点
.3秒后,火箭直线上升到达点  处,此时地面
处,此时地面  处的雷达站测得
处的雷达站测得  处的仰角为
处的仰角为  .已知
.已知  两处相距
两处相距  米,求火箭从
米,求火箭从  到
到  处的平均速度(结果精确到
处的平均速度(结果精确到  米,参考数据:
米,参考数据:  )
)
 处发射、当火箭到达点
处发射、当火箭到达点  时,地面
时,地面  处的雷达站测得
处的雷达站测得  米,仰角为
米,仰角为  .3秒后,火箭直线上升到达点
.3秒后,火箭直线上升到达点  处,此时地面
处,此时地面  处的雷达站测得
处的雷达站测得  处的仰角为
处的仰角为  .已知
.已知  两处相距
两处相距  米,求火箭从
米,求火箭从  到
到  处的平均速度(结果精确到
处的平均速度(结果精确到  米,参考数据:
米,参考数据:  )
) 
如图,楼顶上有一个广告牌AB,从与楼BC相距15 m的D处观测广告牌顶部A的仰角为 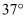 ,观测广告牌底部B的仰角为
,观测广告牌底部B的仰角为  ,求广告牌AB的高度(结果保留小数点后一位,参考数据:
,求广告牌AB的高度(结果保留小数点后一位,参考数据:  ,
,  ,
,  ,
,  ,
, 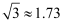 ).
).
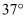 ,观测广告牌底部B的仰角为
,观测广告牌底部B的仰角为  ,求广告牌AB的高度(结果保留小数点后一位,参考数据:
,求广告牌AB的高度(结果保留小数点后一位,参考数据:  ,
,  ,
,  ,
,  ,
, 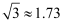 ).
). 
如图,一架无人机静止悬浮在空中P处,小明在山坡A处测得无人机的仰角为  ,小亮在水平地面C处测得无人机的仰角为
,小亮在水平地面C处测得无人机的仰角为  ,已知山坡
,已知山坡  的坡度
的坡度  ,斜坡
,斜坡  长为52米,水平地面
长为52米,水平地面  长为62米,求此时无人机离地面的高度
长为62米,求此时无人机离地面的高度 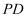 的长.(参考数据:
的长.(参考数据:  )
)
 ,小亮在水平地面C处测得无人机的仰角为
,小亮在水平地面C处测得无人机的仰角为  ,已知山坡
,已知山坡  的坡度
的坡度  ,斜坡
,斜坡  长为52米,水平地面
长为52米,水平地面  长为62米,求此时无人机离地面的高度
长为62米,求此时无人机离地面的高度 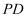 的长.(参考数据:
的长.(参考数据:  )
) 
在一次课外活动中,某数学兴趣小组测量一棵树  的高度.如图所示,测得斜坡
的高度.如图所示,测得斜坡  的坡度
的坡度  ,坡底
,坡底  的长为8米,在
的长为8米,在  处测得树
处测得树  顶部
顶部  的仰角为
的仰角为  ,在
,在  处测得树
处测得树  顶部
顶部  的仰角为
的仰角为  ,求树高
,求树高  .(结果保留根号)
.(结果保留根号)
 的高度.如图所示,测得斜坡
的高度.如图所示,测得斜坡  的坡度
的坡度  ,坡底
,坡底  的长为8米,在
的长为8米,在  处测得树
处测得树  顶部
顶部  的仰角为
的仰角为  ,在
,在  处测得树
处测得树  顶部
顶部  的仰角为
的仰角为  ,求树高
,求树高  .(结果保留根号)
.(结果保留根号)

嵩岳寺塔位于登封市区西北6千米嵩山南麓嵩岳寺院内,为北魏时期佛塔.该塔是我国现存最早的砖塔,反映了中外建筑文化交流融合创新的历程,在结构、造型等方面具有很大价值,对后世砖塔建筑有着巨大影响.某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.

|
课题 |
测量嵩岳寺塔的高度 |
|
|
测量工具 |
测量角度的仪器,皮尺等 |
|
|
测量方案 |
在点C处放置高为1.3米的测角仪CD,此时测得塔顶端A的仰角为45°,再沿BC方向走22米到达点E处,此时测得塔顶端A的仰角为32°. |
说明:点E、C、B三点在同一水平线上. |
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔AB的高度.(精确到0.1米,参考数据: ,
,  ,
,  )
)
最近更新
- 我国是一个历史悠久的农业大国,但各地农业
- 下列各句中加点成语的使用恰当的一组是( �
- 当你遇到下列情况时,你会怎样做,并简要说
- 下列物质中可一次性鉴别乙酸、乙醇、苯和氢
- 完形填空(共20小题;每小题1分,满分20分)
- Most green vegetables, such as spinach cabbage,____ for too
- —How often do you chat with your friends online?—_______
- 把一段确定的导线做成线圈,在确定的磁场中
- 一个同学在进行多边形的内角和计算时,所得
- 某工厂6年来生产某种产品的情况是:前3年年
- 写出通过尺轨作图确定线段AB一个5等分点的算
- 在一块水平固定的光滑板面中心开一个小孔(
- Body language is very important in communication. Studies
- 4p轨道填充一半的元素,其原子序数是( �
- “均衡供求,就是要使物价有高有低,不经
- (2013·天津宝坻高三模拟,5题)利用霍尔效
- 下列饮食习惯中,不正确的是 A.一日三餐,按
- C﹣12和C﹣14是碳元素的两种不同的原子,二者
- 一个三角形的三个内角成等差数列,那么
- 一物体以恒定的加速度由静止开始下落,1s末



