九年级(初三)数学下学期下册试题
已知,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角时90°的扇形ABC(如图),用剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

如图,AB是⊙O的直径,延长AB至点C,使 , CD与⊙O相切于点D.
, CD与⊙O相切于点D. 于点E.
于点E.
 , CD与⊙O相切于点D.
, CD与⊙O相切于点D. 于点E.
于点E.
-
(1) 求证:
 ;
;
-
(2) 点F是直径AB下方⊙O上的一动点(不与点A,B重合),连接FE,FC,FO.
①求
 的值;
的值;②当F运动到何处时?∠OFE的度数最大,请直接写出此时∠OFE的度数.
如果地图上A,B两处的图距是4cm,表示这两地实际的距离是20km,那么实际距离500km的两地在地图上的图距是 cm.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.

-
(1) 求证:CB∥PD;
-
(2) 若BC=3,sin∠BPD=
 ,求⊙O的直径.
,求⊙O的直径.
如图,小敏同学想测量一棵大树的高度 . 她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m , 测得仰角为60°,已知小敏同学身高(AB)为1.6m , 则这棵树的高度为( )(结果精确到0.1m ,  ≈1.73) .
≈1.73) .

A . 3.5m
B . 3.6m
C . 4.3m
D . 5.1m.
小明在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小明所有玩具的进价均2元/个.在销售过程中发现:每天玩具销售量  (件)与销售价格
(件)与销售价格  (元/件)的关系如图所示,其中
(元/件)的关系如图所示,其中  段为反比例函数图象的一部分,
段为反比例函数图象的一部分,  段为一次函数图象的一部分,设小明销售这种玩具的日利润为
段为一次函数图象的一部分,设小明销售这种玩具的日利润为 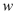 元.
元.
 (件)与销售价格
(件)与销售价格  (元/件)的关系如图所示,其中
(元/件)的关系如图所示,其中  段为反比例函数图象的一部分,
段为反比例函数图象的一部分,  段为一次函数图象的一部分,设小明销售这种玩具的日利润为
段为一次函数图象的一部分,设小明销售这种玩具的日利润为 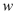 元.
元. 
-
(1) 根据图象,求出
 与
与  之间的函数关系式;
之间的函数关系式;
-
(2) 求销售这种玩具的日利润
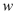 (元)与
(元)与  (元/件)之间的函数关系式,并求每天利润的最大值.
(元/件)之间的函数关系式,并求每天利润的最大值.
如图,直角三角形  纸片中,
纸片中,  ,点
,点  是
是  边上的中点,连接
边上的中点,连接  ,将
,将  沿
沿  折叠,点
折叠,点  落在点
落在点  处,此时恰好有
处,此时恰好有  .若
.若  ,那么
,那么  .
.
 纸片中,
纸片中,  ,点
,点  是
是  边上的中点,连接
边上的中点,连接  ,将
,将  沿
沿  折叠,点
折叠,点  落在点
落在点  处,此时恰好有
处,此时恰好有  .若
.若  ,那么
,那么  .
.

如图是一个正六棱柱,它的俯视图是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
自4月以来,我市推出了一项“共享单车”的便民举措,为人们的城市生活出行带来了方便.图(1)所示的是某款单车的实物图.图(2)是这辆单车的部分几何示意图,其中车支架BC的长为20cm,且∠CBA=75°,∠CAB=30°.求车架档AB的长.(参考数据:sin75°=  ,cos75°=
,cos75°=  ,tan75°=2+
,tan75°=2+  )
)
 ,cos75°=
,cos75°=  ,tan75°=2+
,tan75°=2+  )
)
在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:2,把三角形ABC缩小,得到△AB1C1 , 则点C的对应点C1的坐标为.
如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.( )

A . 40  B . 60﹣20
B . 60﹣20  C . 20
C . 20  D . 20
D . 20
 B . 60﹣20
B . 60﹣20  C . 20
C . 20  D . 20
D . 20
在Rt△ABC中,∠C=90°,如果AC=2,cosA=  ,那么AB的长是( )
,那么AB的长是( )
 ,那么AB的长是( )
,那么AB的长是( )
A . 3
B .  C .
C .  D .
D . 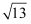
 C .
C .  D .
D . 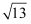
在  中,
中,  是
是  边上的中线,点D在射线
边上的中线,点D在射线  上,过点A作
上,过点A作  交
交  的延长线于点F.
的延长线于点F.
 中,
中,  是
是  边上的中线,点D在射线
边上的中线,点D在射线  上,过点A作
上,过点A作  交
交  的延长线于点F.
的延长线于点F.
-
(1) 如图1,点D在
 边上,
边上,  与
与 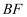 交于点P,证明:
交于点P,证明:  ;
;

-
(2) 如图2,点D在
 的延长线上,
的延长线上,  与
与 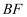 交于点
交于点 
 .
.

①求
 的值;
的值;②若
 ,求
,求  的值
的值
如图在平面直角坐标系xOy中,直线y=﹣  x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
 x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.

-
(1) 如果点Q的速度为每秒
 个单位长度,那么当t=5时,求证:△APQ∽△ABO;
个单位长度,那么当t=5时,求证:△APQ∽△ABO;
-
(2) 如果点Q的速度为每秒2个单位长度,那么多少秒时,△APQ的面积为16?
-
(3) 若点H为平面内任意一点,当t=4时,以点A,P,H,Q四点为顶点的四边形是矩形,请直接写出此时点H的坐标.
如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 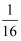 时,则
时,则  为( )
为( )
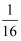 时,则
时,则  为( )
为( ) 
A .  B . 2
C .
B . 2
C . 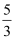 D . 4
D . 4
 B . 2
C .
B . 2
C . 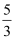 D . 4
D . 4
如图,在  中,
中,  ,
, 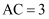 ,
,  ,点D是AB的中点,点P是直线BC上一点,将
,点D是AB的中点,点P是直线BC上一点,将  沿DP所在的直线翻折后,点B落在
沿DP所在的直线翻折后,点B落在  处,若
处,若  ,则点P与点B之间的距离为.
,则点P与点B之间的距离为.
 中,
中,  ,
, 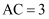 ,
,  ,点D是AB的中点,点P是直线BC上一点,将
,点D是AB的中点,点P是直线BC上一点,将  沿DP所在的直线翻折后,点B落在
沿DP所在的直线翻折后,点B落在  处,若
处,若  ,则点P与点B之间的距离为.
,则点P与点B之间的距离为. 
反比例函数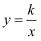 (k≠0)的图象经过点(-2,3),则它还经过点( )
(k≠0)的图象经过点(-2,3),则它还经过点( )
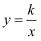 (k≠0)的图象经过点(-2,3),则它还经过点( )
(k≠0)的图象经过点(-2,3),则它还经过点( )
A . (-1,-6)
B . (6,-1)
C . (3,2)
D . (-2,-3)
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )


A . ∠C=∠AED
B . 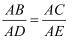 C . ∠B=∠D
D .
C . ∠B=∠D
D . 
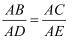 C . ∠B=∠D
D .
C . ∠B=∠D
D . 
如图,为探测某座山的高度AB,某飞机在空中C处测得山顶A处的俯角为31°,此时飞机的飞行高度为CH=4千米;保持飞行高度与方向不变,继续向前飞行2千米到达D处,测得山顶A处的俯角为50°,求此山的高度AB.(参考数据:tan31°≈0.6,tan50°≈1.2)

一个均匀的立方体六个面上分别标有1,2,3,4,5,6,下图是这个立方体表面的展开图,抛掷这个立方体,则朝上一面的数恰好等于朝下一面的数的0.5的概率是( )

A .  B .
B .  C .
C .  D .
D . 
最近更新
- 阅读材料,回答下列问题。 材料一1929年,中国青年学者裴文中发现第一个北京人头盖骨化石,同年又发现用火遗迹。此后,北京
- 多米尼克·莫西伊在采访法国外长于贝尔·韦德里纳时提出:“全球化与美国化是相同的吗?在这个新的全球世界为什么美国似乎是水中
- 有关生物固氮的叙述错误的是( ) A.大气中的氮必须经过生物固氮才能被植物利用 B.土壤中反硝化细菌在氧气不足时,
- 已知函数f(x)=sinxcosx+cos2x.(1)写出函数f(x)的最小正周期和单调递增区间;(2)若函数f(x)的
- 下列实例属于超重现象的是( )A.汽车驶过拱形桥顶端 B.荡秋千的小孩通过最
- 2008年6月20日银行间外汇市场美元对人民币汇率的中间价为1美元对6.88元人民币。随着人民币的升值,一些聪明的消费者
- It is wrong of him to ___________all his friends. A. br
- 如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之
- 周杰伦歌曲《爱在西元前》的歌词写道:“古巴比伦王颁布了……,刻在黑色的玄武岩,距今已经三千七百多年。”请你说出歌词所唱“
- 在中,,则的最大值为
- 分别以“我们生存的物质基底”和“每一个热爱独立思考的人”开头,重组下面两句话。 作为物理学家的爱因斯坦,他的贡献已部分地
- 已知椭圆中心在原点,焦点在x轴上,长轴长等于12,离心率为. (1)求椭圆的标准方程; (2)过椭圆左顶点作直线l,
- 下图为某地地质构造简图,读图判断1~3题。1.图中岩层,最晚形成的是() A.①
- I would appreciate _______ if you could help meget a ticket
- 阅读下面的文言文,完成1~4题。 《范文正公文集》序 苏 轼 庆历三年,轼始总角,入乡校。士有自京师来者,以
- 两个相似多边形,如果它们对应顶点所在的直线______,那么这样的两个图形叫做位似图形.
- 下列关于工业地域的叙述,正确的是( ) A.工业地域都是自发形成的 B.工业集聚而形成的地域,我们称之为工业地域
- 煤作为一种常规能源,随着时代及科技进步,其利用方式有多种多样。读下图,完成1-3题。1.对消费地而言,最清洁且已大规模
- 书面表达(满分25分) 有人说, 父母为孩子包办一切是孩子成长的最大杀手。的确,太多的中国家长习惯于为孩子包办一切。假设
- 分析下表某种大肠杆菌细胞的分子组成,能够做出的推论是 () 成分 水 蛋白质 DNA



