九年级(初三)数学下学期下册试题
如图,已知关于x的函数y=k(x﹣1)和y=  (k≠0),它们在同一坐标系内的图象大致是( )
(k≠0),它们在同一坐标系内的图象大致是( )
 (k≠0),它们在同一坐标系内的图象大致是( )
(k≠0),它们在同一坐标系内的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
有一支夹子如图所示,AB=2BC,BD=2BE,在夹子前面有一个长方体硬物,厚PQ为6cm,如果想用夹子的尖端A、D两点夹住P、Q两点,那么手握的地方EC至少要张开cm.

一个几何体的三视图如图所示,则该几何体可能是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.

如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?(  ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)
已知点P是线段AB的黄金分割点,且PA>PB,若PA=2,AB=x,PB=y,则y与x之间的函数关系式为.
如图,某游乐场一山顶滑梯的高为  ,滑梯的坡角为
,滑梯的坡角为  ,那么滑梯长
,那么滑梯长  为( )
为( )
 ,滑梯的坡角为
,滑梯的坡角为  ,那么滑梯长
,那么滑梯长  为( )
为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,
(1)求证:AC=BD;
(2)若sinC= , BC=36,求AD的长.
, BC=36,求AD的长.

有x个小朋友平均分20个苹果,每人分得的苹果y(每人每个)与x(个)之间的函数关系式为.
如图,在△ABC中,AB=3,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则  的最大值为.
的最大值为.
 的最大值为.
的最大值为. 
如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:  米,
米, 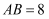 米,
米,  ,
,  ,则
,则  的长为米.(结果保留根号)
的长为米.(结果保留根号)
 米,
米, 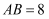 米,
米,  ,
,  ,则
,则  的长为米.(结果保留根号)
的长为米.(结果保留根号) 
一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )

A . 6
B . 8
C . 12
D . 24
下列四个几何体:

其中左视图与俯视图相同的几何体共有( )
A . 1个
B . 2个
C . 3个
D . 4个
如图,铁道路口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高为.(杆的宽度忽略不计)

已知圆锥的母线长为6,侧面积为12  ,则圆锥的半径长为.
,则圆锥的半径长为.
 ,则圆锥的半径长为.
,则圆锥的半径长为.
计算:  .
.
 .
.
下面四组线段中,成比例的是( )
A . a = 2, b = 3, c = 4, d = 5
B . a = 1, b = 2, c = 2, d = 4
C . a = 4, b = 6, c = 5 d = 10
D . a =  , b =
, b =  , c = 3, d =
, c = 3, d = 
 , b =
, b =  , c = 3, d =
, c = 3, d = 
一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.

-
(1) A的对面是,B的对面是,C的对面是;(直接用字母表示)
-
(2) 若A=﹣2,B=|m﹣3|,C=m﹣3n﹣
 , E=(
, E=( +n)2 , 且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
+n)2 , 且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆,则该几何体是( )
A . 圆柱
B . 长方体
C . 圆锥
D . 四棱锥
如图,折叠矩形纸片ABCD时,进行如下操作:①把△BCE翻折使点B落在DC边上的点F处,折痕为CE , 点E在AB边上;②把纸片展开并铺平;③把△CDH翻折使点D落在线段AE上的点G处,折痕为CH , 点H在AD边上.若  ,BC=6,则EG的长为.
,BC=6,则EG的长为.
 ,BC=6,则EG的长为.
,BC=6,则EG的长为. 
最近更新
- 已知1个DNA分子中有8000个碱基对,其中胞嘧啶有4400个,这个DNA分子中应含有的脱氧核苷酸的数目和腺嘌呤的数目分
- 下列关于组成细胞的分子的叙述,正确的是() A. 蔗糖和麦芽糖水解的产物中都有葡萄糖 B.
- 孟德尔利用“假说—演绎法”发现了遗传的基本规律。下列对孟德尔的研究过程的分析中,正确的是() A.孟德尔在豌豆纯合亲本杂
- --- I’m so tired after a whole night work. --- ______ a r
- 糖蛋白在细胞的识别以及细胞内外的信息传导中有重要作用,下列生物结构中,糖蛋白含量最多的是 (
- 英国历史学家J·R·格林说“七年战争是世界历史上的一个转折点,也是我国历史上的一个转折点。”对此理解有误的是( )
- I have afriend named Monty Roberts who owns a horse ranch
- 一位学者这样评价某国政治制度演进:“较少的腥风血雨,较少的声色俱厉……是一路随和,一路感觉,顺着经验走,绕着障碍走,怎么
- 如图所示,在探究串联电路中的电压关系时,小华同学用电压表测出ab、bc、ac两端的电压分别为Uab=2V,Ubc=2V,
- 下列各句中加点的成语使用正确的一项是( ) A. 虽然炎热的夏季早已过去,可怕的秋老虎也已经被秋风赶走,可是特丽珑
- 若|sinxcosx|+|sin2x-cos2x|=,则x= .
- 右图是大西洋部分地区年均逐日从海洋输入大气的总热量分布图(单位:W/m2),导致甲、乙两海区输出热量多少不同的主要因素是
- 纳米材料的表面微粒占总微粒数的比例极大,这是它有许多特殊性质的原因。假设某氯化钠纳米颗粒的大小和形状恰好与氯化钠晶胞的大
- 下列关于氧气的说法中错误的是 A. 氧气能支持燃烧,可作燃料 B. 空气成分中氧气约占空气体积的21% C. 水中的生物
- (12分)如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:(1)将点B向右移动三个单位长度后到达点D,
- 以下二倍体生物的细胞中含有两个染色体组的是( ) ①有丝分裂中期细胞 ②有丝分裂后期细胞 ③减数第
- 高中生小杨所在的研究性学习小组,想给当地政府有关负责人写一份《关于提升政府权威的建议书》。他们列出的建议中有以下几点,你
- 吴某是一家国有企业工程师,去年工资收入是36000元,奖金8000元,个人专利转让收入5000元;其妻开一家个体杂货店,
- 图甲是果醋发酵装置。发酵初期不通气,溶液中有气泡产生;中期可以闻到酒香;后期接种醋酸菌,适当升高温度并通气,酒香逐渐变
- 下列关于科学实验的“操作—现象—结论”的描述正确的是() A.在某固体物质中加入稀盐酸,产生大量气泡,该物质一定是碳酸盐



