九年级(初三)数学下学期下册试题
一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最少是( )

A . 3
B . 4
C . 5
D . 6
下面四个关系中,y是x的反比例函数的是( )
A .  B . yx=-
B . yx=-  C . y=5x+6
D .
C . y=5x+6
D . 
 B . yx=-
B . yx=-  C . y=5x+6
D .
C . y=5x+6
D . 
-
(1) 计算:
 +20190+
+20190+ 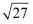 ﹣2cos30°
﹣2cos30°
-
(2) 先化简,再求值,
 ÷
÷  ﹣
﹣  ,其中a=﹣5.
,其中a=﹣5.
如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为.

如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F.

-
(1) 求证:直线EF是⊙O的切线;
-
(2) CF=5,cos∠A=
 ,求AE的长.
,求AE的长.
如图,DE∥BC,且过△ABC的重心,分别与AB,AC交于点D,E,点P是线段DE上一点,CP的延长线交AB于点Q,如果  =
=  ,那么S△DPQ:S△CPE的值是.
,那么S△DPQ:S△CPE的值是.
 =
=  ,那么S△DPQ:S△CPE的值是.
,那么S△DPQ:S△CPE的值是. 
在4×4网格中,∠α的位置如图所示,则tan  的值为( )
的值为( )
 的值为( )
的值为( ) 
A .  B .
B .  C . 2
D .
C . 2
D . 

 B .
B .  C . 2
D .
C . 2
D . 
在一盏路灯的周围有一圈栏杆,则下列叙述中不正确的是( )
A . 若栏杆的影子落在围栏里,则是在太阳光照射下形成的
B . 若这盏路灯有影子,则说明是在白天形成的影子
C . 若所有的栏杆的影子都在围栏外,则是在路灯照射下形成的
D . 若所有的栏杆的影子都在围栏外,则是在太阳光照射下形成的
如图,a∥b∥c,
(1)若AC=6cm,EC=4cm,BD=8cm,则线段DF的长度是多少厘米?
(2)若AE:EC=5:2,DB=5cm,则线段DF的长度是多少厘米?

如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

如图,在  中,D、E分别为AB、AC边上的点,
中,D、E分别为AB、AC边上的点,
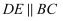 ,BE与CD相交于点F,则下列结论一定正确的是( )
,BE与CD相交于点F,则下列结论一定正确的是( )
 中,D、E分别为AB、AC边上的点,
中,D、E分别为AB、AC边上的点,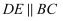 ,BE与CD相交于点F,则下列结论一定正确的是( )
,BE与CD相交于点F,则下列结论一定正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在矩形ABCD中,AB=4,BC=2.点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是.

如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.

-
(1) 求∠CBA的度数.
-
(2) 求出这段河的宽(结果保留根号).
如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和10米.已知小华的身高为1.6米,那么他所住楼房的高度为( )
A . 8米
B . 16米
C . 32米
D . 48米
如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=  的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( ) 
A . 72
B . 36
C . 16
D . 9
抛物线y=a(x-3)(x+1)与x轴交于点A,B(点A在点B的左边),与y轴交于点C(0,-2),过点C作x轴的平行线交抛物线于点D,连D0,并延长交抛物线于点E,点P是∠CDE内的抛物线CE之间部分上的动点,过P点作PF⊥CD于点F,PG⊥DE于点G,点H为PG的中点,连FH,DP。当FH⊥DP时,点P的坐标是
.

我校的北大门是由相同菱形框架组成的伸缩电动推拉门,如图是大门关闭时的示意图,此时 菱形的边长为0.5m,锐角都是50°.求大门的宽(结果精确到0.01,参考数据:sin25°≈0.422 6,cos25°≈0.906 3).

小华同学将笔记本电脑水平放置在桌子上,当是示屏的边缘线  与底板的边缘线
与底板的边缘线  所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,
所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,  ,
,  ,
,  .
.
 与底板的边缘线
与底板的边缘线  所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,
所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,  ,
,  ,
,  .
. 
-
(1) 求
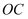 的长;
的长;
-
(2) 如图④,垫入散热架后,要使显示屏的边缘线
 与水平线的夹角仍保持120°,求点
与水平线的夹角仍保持120°,求点 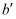 到
到  的距离.(结果保留根号)
的距离.(结果保留根号)
由5个相同的小正方体搭成的几何体如图所示,则它的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知圆锥底面圆的半径为6cm,它的侧面积为60πcm2 , 则这个圆锥的高是 cm.
最近更新
- 一物体m受到一个撞击力后沿光滑斜面向上滑动,如图所示,在滑动过程中,物体m受到的力是( )
- 热化学方程式:C(s)+H2O(g)CO(g)+H2(g) ΔH=+131.3kJ/mol和H(g)+H(g)===H
- 环渤海经济区包括辽宁、河北、北京、天津、山东5省市,是继珠江三角洲、长江 三角洲后又一个经济快速发展的地区。读图,回
- 记一个两位数的个位数字与十位数字的和为A.若A是不超过5的奇数,则从这些两位数中任取一个,其个位数为1的概率为.
- 下图是家蚕个体发育过程中的四种虫态图,请据图回答。(1)家蚕个体发育正确顺序是
- 表示一个地区人口疏密程度的是: A.人口总数的多少 B.人口居住面积的大小 C.人口的自然增长率 D.人口密度
- 下列史实最早发生在武汉的有 ①中国第一个近代化钢铁工厂 ②发起二次革命 ③建立国民政府 ④
- (16分)联合国第63届大会决定将2011年作为国际化学年(IYC2011),其主题是“化学——人类的生活,人类的未来”
- After the long journey, the three of them went back home, __
- 如图表示一个由三条多肽链形成的蛋白质分子,共含271个氨基酸,图中每条虚线表示由两个R基中的硫基(﹣SH)脱氢形成一个二
- 下列叙述中,错误的是 A.正常情况下,细胞分裂可以无限进行下去 B.癌细胞具有无限增殖的特点 C.高度分化的细胞有可能永
- This couple have strange habits . He’d like to sleep with la
- 关于我国水资源时空分布的说法,正确的是 A.夏秋多、冬春少
- 在△ABC中,点P在BC上,且=2,点Q是AC的中点,若=(4,3),=(1,5),则=.
- 下列有关水的叙述中,错误的是() ①参与运输营养物质和代谢废物的水为自由水 ②生物体内的化学反应离不开水 ③水是细胞结构
- 中国古代封建官制取代世袭制,适应了君主专制的需要,主要是因为( )A.拓宽了官吏的选拔途径 B.扩大了统治
- 2011年3月至6月,湖北省委集中开展了“万名干部进万村人万户”活动 (简称 “三万”活动),10万多名干部进村入户
- 下列物质的分类合理的是 () A.酸:HNO3、H2SO4、
- 直线2x-y+9=0和直线4x-2y+1=0的位置关系是 () A.平行
- Weknow a lot about these early years of European settlement



