九年级(初三)数学下学期下册试题
有一轮船由东向西航行,在A处测得西偏北15°有一灯塔P.继续航行20海里后到B处,又测得灯塔P在西偏北30°.如果轮船航向不变,则灯塔与船之间的最近距离是海里.
如图:一次函数的图象与反比例函数  的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)
 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n) 
-
(1) 求反比例函数的解析式和B点坐标
-
(2) 根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
如图,河堤横断面如图所示,迎水坡AB的坡比为1: ,则坡角∠A的度数为
,则坡角∠A的度数为
在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12  米,CD=6米,∠D=30°,(其中点A , B , C , D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
米,CD=6米,∠D=30°,(其中点A , B , C , D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
 米,CD=6米,∠D=30°,(其中点A , B , C , D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
米,CD=6米,∠D=30°,(其中点A , B , C , D均在同一平面内)则垂直升降电梯AB的高度约为( )米. 
A . 10  B . 10
B . 10  ﹣12
C . 12
D . 10
﹣12
C . 12
D . 10  +12
+12
 B . 10
B . 10  ﹣12
C . 12
D . 10
﹣12
C . 12
D . 10  +12
+12
如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则下列结论:
①AE=BF;②S四边形ECFG=S△ABG;③△BFQ是等腰三角形;④  .
.
其中一定正确的个数是( )

A . 1个
B . 2个
C . 3个
D . 4个
已知点(3,﹣1)在反比例函数  的图象上,则下列各点也在该反比例函数图象上的是( )
的图象上,则下列各点也在该反比例函数图象上的是( )
 的图象上,则下列各点也在该反比例函数图象上的是( )
的图象上,则下列各点也在该反比例函数图象上的是( )
A . (1,3)
B . (﹣3,﹣1)
C . (﹣1,3)
D . (3,1)
已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.

如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )

A . (0,0)
B . (0,1)
C . (1,﹣1)
D . (1,0)
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )

A . 美
B . 丽
C . 萃
D . 县
作图与推理:如图,是由一些大小相同的小正方体组合成的简单几何体

-
(1) 图中有块小正方体;
-
(2) 从正面看到该几何体的形状图如图所示,请在下面方格纸中分别画出从左面,上面看到该几何体的形状图
已知:∠A为锐角,且cosA≥ , 则( )
, 则( )
 , 则( )
, 则( )
A . 0°<∠A≤60°
B . 60°≤∠A<90°
C . 0°<∠A≤30°
D . 30°≤∠A<90°
如图,在  中,
中,  ,
,  于点
于点  ,则下列结论不正确的是( ).
,则下列结论不正确的是( ).
 中,
中,  ,
,  于点
于点  ,则下列结论不正确的是( ).
,则下列结论不正确的是( ). 
A . 
 B .
B .  C .
C . 
 D .
D . 

 B .
B .  C .
C . 
 D .
D . 
如图,l1∥l2∥l3 , 直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若  ,DE=4,则EF的长是( )
,DE=4,则EF的长是( )
 ,DE=4,则EF的长是( )
,DE=4,则EF的长是( ) 
A . 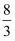 B .
B . 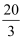 C . 6
D . 10
C . 6
D . 10
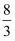 B .
B . 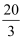 C . 6
D . 10
C . 6
D . 10
如图,大楼AB高16米,远处有一塔CD,某人在楼底B处测得塔顶的仰角为38.5°,爬到楼顶A处测得塔顶的仰角为22°,求塔高CD及大楼与塔之间的距离BD的长.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )

如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我航海区域的C处截获可疑渔船,问我渔政船的航行路程是海里(结果保留根号).

若 , 则反比例函数
, 则反比例函数 与一次函数
与一次函数 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
 , 则反比例函数
, 则反比例函数 与一次函数
与一次函数 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算: 

如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?

如图,某校教学楼  的后面有一建筑物
的后面有一建筑物  ,当光线与地面的夹角是
,当光线与地面的夹角是  时,教学楼在建筑物的墙上留下高2米的影子
时,教学楼在建筑物的墙上留下高2米的影子 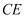 ;而当光线与地面夹角是
;而当光线与地面夹角是  时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B , F , C在一条直线上),求教学楼
时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B , F , C在一条直线上),求教学楼  的高结果保留整数).参考数据:
的高结果保留整数).参考数据:  .
.
 的后面有一建筑物
的后面有一建筑物  ,当光线与地面的夹角是
,当光线与地面的夹角是  时,教学楼在建筑物的墙上留下高2米的影子
时,教学楼在建筑物的墙上留下高2米的影子 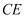 ;而当光线与地面夹角是
;而当光线与地面夹角是  时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B , F , C在一条直线上),求教学楼
时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B , F , C在一条直线上),求教学楼  的高结果保留整数).参考数据:
的高结果保留整数).参考数据:  .
. 
某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l(即AD+AB+BC的长).

最近更新
- 下列实验能获得成功的是() A.将乙醛滴入银氨溶液中,加热煮沸制银镜 B.苯与浓溴水反应制取溴苯 C.向浓溴水中加几滴苯
- 下列有关文学常识的表述有误的一项是( ) A.词,兴于隋唐,盛于两宋,又称“曲子”、“曲子词”、“诗余”、“长短句
- 在谈到要根据形势的变化增强政策的针对性和灵活性时,温家宝总理引用古语“时进则进,时退则退,动静不失其时”。此古语蕴含的主
- 一个圆锥形的零件的母线长为4,底面半径为1,则这个圆锥形零件的全面积是 .
- (7分).下图是周期表中短周期的一部分,A.B.C三种元素的原子核外电子数之和等于B的质子数的2倍。1、(用元素符号表示
- 实验桌上有两只大烧杯,其中一杯盛有纯净水,另一杯盛有盐水。老师告诉小敏盐水的密度大于纯净水的密度,希望她用压强计将它们区
- It ______ be thevocabulary that caused you the problem in t
- The international human rights NGO, Lightfor the World, anno
- 右图为血糖调节模型,下列判断中正确的是A.激素甲的分泌细胞是胰岛A细胞 B.激素乙的分泌细胞是胰岛B细胞 C.激素乙是胰
- —Did you go to visit the Acropolisyesterday? —Ihad meant to,
- 甲、乙两个物体的质量分别为和,并且=2,它们与水平桌面的动摩擦因数相同,当它们以相同的初动能在桌面上滑动时,它们滑行的最
- (1)古代戏剧以“戏”和“曲”为主要因素,称为“戏曲”,主要包括 、杂剧、传奇以及各种地方戏,
- 关于反比例函数的图象,下列说法正确的是( )A.必经过点(1,1)
- Injuries anddeaths caused by driving after drinking are prev
- 右图是某个化学反应前后各种物质微观模拟图, 图中“”“”表示不同元素的原子。根据图 示判断,该反应属于 反应
- 美国的金门大桥是“4+4”八车道模式,由于上下班车流在不同时段出现两个半边分布不均的现象,桥上经常发生堵车问题。一个年轻
- I'm terribly sorry to have kept you waiting so long, but it'
- 设NA为阿伏加德罗常数的值,下列有关说法正确的是 A.1 mol苯分子中含有C=C双键数为3NA B.1 mol甲基
- 若a的相反数是最大的负整数,b的绝对值为2,则a+b=__________.
- 我省生产的奇瑞A3汽车油箱的容量为55L。已知汽油的热值q=3.7×107J/L,则一箱汽油完全燃烧能释放的热量为



