九年级(初三)数学下学期下册试题
根据要求完成下列题目.

-
(1) 图中有块小正方体.
-
(2) 请在方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影).
-
(3) 用小正方体搭一几何体,使得它的俯视图和左视图与你在下图方格中所画的图一致,则这样的几何体最少要个小正方体,最多要个小正方体.
如图,直线  ,直线
,直线 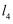 ,
,  被
被  ,
,  ,
,  所截,截得的线段分别为
所截,截得的线段分别为  ,
,  ,
,  ,
,  .若
.若 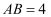 ,
,  ,
,  ,则
,则  的长是( )
的长是( )
 ,直线
,直线 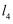 ,
,  被
被  ,
,  ,
,  所截,截得的线段分别为
所截,截得的线段分别为  ,
,  ,
,  ,
,  .若
.若 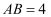 ,
,  ,
,  ,则
,则  的长是( )
的长是( ) 
A . 4
B . 4.5
C . 5
D . 5.5
某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“青”字所在面相对的面上的汉字是( )

A . 青
B . 春
C . 梦
D . 想
如图,白炽灯正下方有一个乒乓球,当乒乓球沿竖直方向越来越远离白炽灯时,它在地面上的影子( )

A . 越来越大
B . 越来越小
C . 先变大后变小
D . 先变小后变大
如图,以原点为圆心的圆与反比例函数y= 的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
 的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
A . -3
B . -2
C . -1
D . -4
如图,已知OB的方向是南偏东60°,OA、OC分别平分∠NOB和∠NOE,

-
(1) 请直接写出OA的方向是,OC的方向是.
-
(2) 求∠AOC的度数.
(材料阅读)2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度,其基本原理之一是三角高程测量法,在山顶上立一个标杆,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300m时,还要考虑球气差,球气差计算公式为  (其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.
(其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.
 (其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.
(其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差. (问题解决)某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图,点A,B的水平距离d=800m,测量仪AC=1.5m,觇标DE=2m,点E,D,B在垂直于地面的一条直线上,在测量点A处用测量仪测得山顶标杆顶端E的仰角为37°,测量点A处的海拔高度为1800m.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).请你计算该山的海拔高度(要计算球气差,结果精确到0.01m).

北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为 丈.

如图,点A在曲线到 上,点B在双曲线
上,点B在双曲线 上,AB
上,AB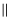 x轴,点C是x轴上一点,连接
x轴,点C是x轴上一点,连接 、
、 , 若
, 若 的面积是6,则k的值为.
的面积是6,则k的值为.
 上,点B在双曲线
上,点B在双曲线 上,AB
上,AB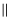 x轴,点C是x轴上一点,连接
x轴,点C是x轴上一点,连接 、
、 , 若
, 若 的面积是6,则k的值为.
的面积是6,则k的值为.
如图,  是
是  的直径,过O作弦AC的垂线,交
的直径,过O作弦AC的垂线,交  于点D,分别交AE、AC于点E、点F,已知
于点D,分别交AE、AC于点E、点F,已知  .
.
 是
是  的直径,过O作弦AC的垂线,交
的直径,过O作弦AC的垂线,交  于点D,分别交AE、AC于点E、点F,已知
于点D,分别交AE、AC于点E、点F,已知  .
. 
-
(1) 判断AE与
 的位置关系,并说明理由;
的位置关系,并说明理由;
-
(2) 若
 ,
,  ,求
,求  的长.
的长.
已知反比例函数  的图象位于第二、四象限,
的图象位于第二、四象限,  两点在该图象上,下列命题:
两点在该图象上,下列命题:
 的图象位于第二、四象限,
的图象位于第二、四象限,  两点在该图象上,下列命题:
两点在该图象上,下列命题: ①过点  作
作  轴,
轴,  为垂足,连结OA.若
为垂足,连结OA.若  的面积为3,则
的面积为3,则  ;②若
;②若  ,则
,则  ;③若
;③若  ,则
,则  .其中真命题个数是( )
.其中真命题个数是( )
A . 0
B . 1
C . 2
D . 3
如图,点A在反比例函数  的图象上,过点A作
的图象上,过点A作  轴,垂x足为点B,点C在y轴上,则
轴,垂x足为点B,点C在y轴上,则  的面积为( )
的面积为( )
 的图象上,过点A作
的图象上,过点A作  轴,垂x足为点B,点C在y轴上,则
轴,垂x足为点B,点C在y轴上,则  的面积为( )
的面积为( ) 
A . 3
B . 2
C . 1.5
D . 1
如图是由八个相同小正方体组合而成的几何体,其俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,四边形ABCD是正方形,点E , F 分别在边 , BC 上,且CE=DF ,DE ,AF 交于点G ,AF的中点为点H ,连接BG ,DH ,现有以下结论:①
 ;②
;②


 ;③
;③
 ;④
;④


 .其中正确的结论有.(填写所有正确结论的序号)
.其中正确的结论有.(填写所有正确结论的序号)
 ;②
;②


 ;③
;③
 ;④
;④


 .其中正确的结论有.(填写所有正确结论的序号)
.其中正确的结论有.(填写所有正确结论的序号)

如图所示物体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
下列函数中,y可以看作是x的反比例函数的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列几何体中,从正面看到的形状为三角形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,四边形  与四边形
与四边形 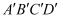 位似,点O为位似中心,已知
位似,点O为位似中心,已知  ,则四边形
,则四边形  与四边形
与四边形 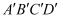 的面积比为( )
的面积比为( )
 与四边形
与四边形 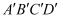 位似,点O为位似中心,已知
位似,点O为位似中心,已知  ,则四边形
,则四边形  与四边形
与四边形 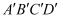 的面积比为( )
的面积比为( ) 
A . 1:4
B . 1:2
C . 1:9
D . 1:3
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线  的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题: 
-
(1) 恒温系统在这天保持大棚内温度18℃的时间有多少小时?
-
(2) 求k的值;
-
(3) 当x=16时,大棚内的温度约为多少度?
如图,直线l1∥l2∥l3 , 直线AC依次交l1 , l2 , l3于A,B,C三点,直线DF依次交l1 , l2 , l3于D,E,F三点,若
 ,DE=12,求EF的长.
,DE=12,求EF的长.
 ,DE=12,求EF的长.
,DE=12,求EF的长.

最近更新
- 2012年3月22日是第二十届“世界水日”,3月22-28日是第二十五届“中国水周”。 联合国确定今年 “世界水日”的
- 关于x的不等式组的所有整数解的和是-7,则m的取值范围是_______
- 1.那儿的人们怎么样? How ___________ the people there? 2.那个孩子迷路了,我们帮他
- 下列四种物质的溶液,其中一种与其它三种能发生离子反应,这种物质是( ) A.BaCl2 B.KOH
- 下列变化属于物理变化的是() A.铁钉生锈 B.干冰升华 C.呼吸作用 D.食物腐败
- 下列抗生素药品中属于真菌产生的是( ) A.青霉素
- 求满足下列条件的双曲线方程(1)以2x±3y=0为渐近线,且经过点(1,2);(2)离心率为,虚半轴长为2;(3)与椭圆
- 科学家发现银河系中存在大量的放射性同位素铝26 。 铝26的半衰期为 72 万年,其衰变方程为 ,下列说法正确的是(
- An unhealthy obsession (着迷)with celebrity(名人) culture is dam
- 请用三个四字短语来概括《边城》的主人公翠翠的性格特征。
- 图1为甲、乙、丙、丁四国人口增长状况图,图2为不同阶段人口发展模式图。读图回答1~2题。 1.图1中四个国家人口增长特点
- 列宁主义诞生的历史条件是:( )。 ①19世纪70年代,俄国无产阶级登上历史舞台 ②普列汉诺夫积极传播马克思主义
- 君主立宪制的含义是什么?在这种制度下君主的权力发生了什么变化?
- 2009年4月22日清晨,金星、火星出现在东方低空,金星、火星这对夜空最明亮的星星与一弯细细的娥眉月相依相偎,远看犹如一
- When she wants to be picked ______, Washsoe points up with o
- 选出下列句子中表达得体的一项 ( ) A.
- Don’tworry. Let me _______ you after _______. A. to help;
- 阅读下面的文字,根据要求作文。(60分) 各位朋友: 我们是环球享乐公司的代表,我们的宗旨是让您快乐地度过这一生,
- 一物体运动的v﹣﹣t图象如图所示,设向右为正,下列关于前4s内物体运动情况的判断,下列说法正确的是( )
- 单项填空 Peteris 15 years old. He is __________ than his father.



