九年级(初三)数学下学期下册试题
已知圆锥的底面半径为7cm,它的侧面积是35πcm,则这个圆锥的母线长为.
已知两个相似三角形的周长比为4:9,则它们的面积比为( )
A . 4:9
B . 2:3
C . 8:18
D . 16:81
下列四个几何体中,左视图为圆的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA的值为( )
A .  B .
B .  C .
C .  D . 以上都不对
D . 以上都不对
 B .
B .  C .
C .  D . 以上都不对
D . 以上都不对
如图,是反比例函数 的图象的一个分支,对于下列说法:
的图象的一个分支,对于下列说法:
①常数k的取值范围是k>5;
②图象的另一个分支在第四象限;
③在函数图象上取点A(a1 , b1)和B(a2 , b2),当a1>a2时,则b1>b2;
④在函数图象的某一个分支上取点A(a1 , b1)和B(a2 , b2),当a1>a2时,则b1>b2;
其中正确的是( )

A . ①②③④
B . ①②③
C . ②③④
D . ①②④
如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是.

如图,一块矩形ABCD绸布的长AB=a,宽AD=1,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )

A .  B .
B .  C . 2
D .
C . 2
D . 
 B .
B .  C . 2
D .
C . 2
D . 
已知函数  是反比例函数.
是反比例函数.
 是反比例函数.
是反比例函数.
-
(1) 求m的值;
-
(2) 求当
 时,y的值
时,y的值
下面几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,A是反比例函数  的图象上一点,过点A作AB∥y轴交反比例函数
的图象上一点,过点A作AB∥y轴交反比例函数  的图象交于点B,已知△OAB的面积为5,则k的值为.
的图象交于点B,已知△OAB的面积为5,则k的值为.
 的图象上一点,过点A作AB∥y轴交反比例函数
的图象上一点,过点A作AB∥y轴交反比例函数  的图象交于点B,已知△OAB的面积为5,则k的值为.
的图象交于点B,已知△OAB的面积为5,则k的值为. 
先化简,再求值:  ,其中a=2tan60°•sin30°.
,其中a=2tan60°•sin30°.
 ,其中a=2tan60°•sin30°.
,其中a=2tan60°•sin30°.
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
, 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设 ,
,  ,
,  .
.
 , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
, 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设 ,
,  ,
,  .
. 
特例探索
-
(1) ①如图1,当
 ,
,  时,
时,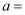 ▲ ,
▲ , 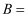 ▲ ;
▲ ;②如图2,当
 ,
,  时,求a和b的值.
时,求a和b的值. -
(2) 请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
-
(3) 利用(2)中的结论,解答下列问题:
在菱形ABCD中,对角线
 ,
,  , O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求
, O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求 的值.
的值.
-
(1) 计算:
 ;
;
-
(2) 先化简,再求值:
 ,其中
,其中  .
.
如图,在△ABC中,点D是边AB上的一点,∠ACD=∠B,AD=2,BD=6,则边AC的长为.

如图,已知△ABC中AD⊥BC于D,BE⊥AC于E.

-
(1) 求证:△CDE
 △CAB.
△CAB.
-
(2) 若∠C=60°,求S△CDE:S△CAB的值.
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )

A . 7个
B . 8个
C . 9个
D . 10个
如图,直线  ,直线m , n分别与a , b , c相交于点A , B , C , D , E , F , 若
,直线m , n分别与a , b , c相交于点A , B , C , D , E , F , 若  ,
, 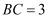 ,
,  ,则
,则  .
.
 ,直线m , n分别与a , b , c相交于点A , B , C , D , E , F , 若
,直线m , n分别与a , b , c相交于点A , B , C , D , E , F , 若  ,
, 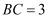 ,
,  ,则
,则  .
. 
如图所示几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:

-
(1) 矩形奇妙四边形(填“是”或“不是”);
-
(2) 如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为8,∠BCD=60°.求奇妙四边形ABCD的面积;
-
(3) 如图3,已知⊙O的内四边形ABCD是奇妙四边形,作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于( )
A . 11π
B . 10π
C . 9π
D . 8π
最近更新
- “小时不识月,呼作白玉盘。又疑瑶台镜,飞在青云端。”看到月亮,一个小孩会形象地把它同日常生活中得某些东西联系起来;而一个
- It’s impolite ___ you to ask one’s private affairs. A. for
- 柳宗元认为,秦末农民起义“咎在人怨,非郡邑之制失也”;西汉七国之乱“有叛国而无叛郡”,“秦制之得亦明矣”。下列哪种说法最
- Our kind teacher wanted to teach us _____ he knew athis less
- 中国运动员获得的第一枚奥运会金牌是在A.第23届洛杉矶奥运会上B.第27届悉尼奥运会上C.第28雅典届奥运会上D.第29
- 但丁被誉为“旧时代的最后一位诗人,新时代的最初一位诗人。”开辟这个“新时代”的是A.文艺复兴运动 B.启蒙运动
- 一定条件下,水在密闭容器里的冷却过程中,温度和时间的关系如下图所示,①、②、③表示水在不同时刻的存在状态,下列说法正确的
- Having a trip abroad is certainly good for the old couple, b
- 下图为某河流示意图,读图回答问题。关于图示河流所在国工业的叙述,正确的是
- 下列各项与蛋白质的作用无关的是() A.催化与调节 B.运动 C.运送物质 D.储存遗传信息
- (1)某兴趣小组为测一遥控电动小车的额定功率,进行了如下实验: ①用天平测出电动小车的质量为0.4 kg;②将电动小车、
- 下图是桃的果实结构示意图,据此可判断桃属于()A.藻类植物 B.蕨类植物 C.裸子植物
- 更好地完善自我,“吾日三省我身”,这是对自我负责;经营者生产价廉质优的商品,诚实守信,这是对消费者负责;报纸杂志撰文真实
- 我国古代出现了很多政治清明、经济发达、文化繁荣的治世局面。下列的繁荣局面与唐太宗在位时期有关的是A.开皇之治B.贞观之治
- 洗发产品中含有的柠檬酸(C6H8O7)能使头发柔顺有弹性且气味清香.下列关于柠檬酸的说法中正确的是() A.柠檬酸属于氧
- “X基因”是DNA分子上一个有遗传效应的片段,若要用PCR技术特异性地拷贝“X基因”,需在PCR反应中加入引物1和引物2
- (2012年3月山东省淄博市一模)矩形导线框abcd放在匀强磁场中静止不动,磁场方向与线圈平面垂直,磁感应强度B随时间t
- Every personhas its own way of saying things, and it’s their
- 曹操《短歌行》中引古起兴,婉转吐露求贤才而不得时日夜思慕之情的诗句是“____________,悠悠我心。_______
- 俄罗斯专家发现图中标示的某种地理事物与实际分布不符。它是( )A. B. C.



