九年级(初三)数学下学期下册试题
如图是在写字台上放置一个折叠式台灯时的截面示意图,已知台灯灯管  长40
长40  ,灯杆
,灯杆  长50
长50  ,台灯灯管、灯杆的夹角即
,台灯灯管、灯杆的夹角即  ,灯杆
,灯杆  与写字台
与写字台  的夹角即
的夹角即  .
.
 长40
长40  ,灯杆
,灯杆  长50
长50  ,台灯灯管、灯杆的夹角即
,台灯灯管、灯杆的夹角即  ,灯杆
,灯杆  与写字台
与写字台  的夹角即
的夹角即  .
. 
-
(1) 求台灯灯管
 与水平线的夹角(锐角)?
与水平线的夹角(锐角)?
-
(2) 求灯管顶端E到写字台
 的距离,即
的距离,即  的长?(台灯底座的宽度、高度都忽略不计,A , F , C , B在同一条直线上,参考数据:
的长?(台灯底座的宽度、高度都忽略不计,A , F , C , B在同一条直线上,参考数据:  ,
,  ,
,  ;结果精确到0.1
;结果精确到0.1  )
)
如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC﹣CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).

-
(1) 当点F在边QH上时,求t的值;
-
(2) 当正方形PDEF与△QGH重叠部分图形是四边形时,求S与t之间的函数关系式;
-
(3) 当FH所在的直线平行或垂直于AB时,直接写出t的值.
如图,  ,
,  ,若
,若  ,则CE的长是( )
,则CE的长是( )
 ,
,  ,若
,若  ,则CE的长是( )
,则CE的长是( ) 
A .  B . 2
C .
B . 2
C . 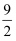 D . 5
D . 5
 B . 2
C .
B . 2
C . 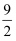 D . 5
D . 5
如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=  ,那么当点P运动一周时,点Q运动的总路程为.
,那么当点P运动一周时,点Q运动的总路程为.

计算或化简:
-
(1) 计算:

-
(2) 化简:

如图,  ,
, 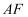 与
与  相交于点
相交于点  ,若
,若  ,
,  ,
,  ,则
,则  的值是( )
的值是( )
 ,
, 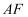 与
与  相交于点
相交于点  ,若
,若  ,
,  ,
,  ,则
,则  的值是( )
的值是( ) 
A .  B .
B .  C .
C . 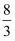 D .
D . 
 B .
B .  C .
C . 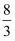 D .
D . 
如图,锐角△ABC内接于⊙O,AB=AC,BD为直径,过点B作BF⊥AB交⊙O于点E,交DC的延长线于点F.

-
(1) 求证:∠ABD=∠CBF.
-
(2) 连结DE,若DE=20,sin∠A=
 ,求BF的长.
,求BF的长.
如图,某个反比例函数的图象经过点P,则它的解析式为( )

A . y=  (x>0)
B . y=-
(x>0)
B . y=-  (x>0)
C . y=
(x>0)
C . y=  (x<0)
D . y=-
(x<0)
D . y=-  (x<0)
(x<0)
 (x>0)
B . y=-
(x>0)
B . y=-  (x>0)
C . y=
(x>0)
C . y=  (x<0)
D . y=-
(x<0)
D . y=-  (x<0)
(x<0)
如图,一船以每小时36海里的速度向正北航行到A处,发现它的东北方向有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在它的北偏东75°方向,则此时船与灯塔的距离为( )

A . 24
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为,当S=2 cm2时, R=(Ω)

计算:  |.
|.
 |.
|.
如图,△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.

-
(1) 求证:直线AC是⊙O的切线;
-
(2) 如果∠ACB=75°,⊙O的半径为2,求BD的长.
如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )

A . 
B .
B . 
C .
C . 
D .
D . 

B .
B . 
C .
C . 
D .
D . 
计算题:  ﹣3+(3.14﹣π)0﹣(5
﹣3+(3.14﹣π)0﹣(5  ﹣3)+2sin30°
﹣3)+2sin30°
 ﹣3+(3.14﹣π)0﹣(5
﹣3+(3.14﹣π)0﹣(5  ﹣3)+2sin30°
﹣3)+2sin30°
如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2米.若梯子与地面的夹角为  ,则梯子顶端到地面的距离(BC的长)为( )
,则梯子顶端到地面的距离(BC的长)为( )
 ,则梯子顶端到地面的距离(BC的长)为( )
,则梯子顶端到地面的距离(BC的长)为( ) 
A .  米
B .
米
B .  米
C .
米
C .  米
D .
米
D .  米
米
 米
B .
米
B .  米
C .
米
C .  米
D .
米
D .  米
米
如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和相等,则  .
.
 .
. 
如图是一个正方体骰子的表面展开图,请根据要求回答问题:
(1)如果1点在上面,3点在左面,几点在前面?
(2)如果5点在下面,几点在上面?

如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 

如图,已知抛物线  经过
经过  ABC的三个顶点,其中点A(0,1),点B(-9,10),
ABC的三个顶点,其中点A(0,1),点B(-9,10),  轴,点P是直线AC下方抛物线上的动点.
轴,点P是直线AC下方抛物线上的动点.
 经过
经过  ABC的三个顶点,其中点A(0,1),点B(-9,10),
ABC的三个顶点,其中点A(0,1),点B(-9,10),  轴,点P是直线AC下方抛物线上的动点.
轴,点P是直线AC下方抛物线上的动点. 
-
(1) 直接写出:b= ,c=;
-
(2) 过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;
-
(3) 当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与
 ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.
ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.
如图,正方形ABOC的边长为2,反比例函数y= 的图象过点A,则k的值是( )
的图象过点A,则k的值是( )
A . 2
B . ﹣2
C . 4
D . ﹣4
最近更新
- 向如图试管里的水中加入下述某种物质后,原来U型管内在同一水平上的红墨水,右边液面降低了些,左边液面上升了些,则加入的物质
- It was a very foggy day inLondon Mr. Smith from Edinburg
- All the debts be paid off by the end of the month, o
- 如图A-6所示电路中电阻R1、R2、R3的阻值相等,电池的内阻不计.那么,开关S接通后,流过R2的电流是S接通前的___
- 阅读下面的文字,完成下题。 窗中戏剧 女人倚在窗子边,朝对面望去。风微微地从河边吹来,感觉和平常没什么不一样。她住在顶楼
- ,其中
- 读“不同纬度山地垂直自然带分布示意图”。 甲山地苔原带分布的海拔高度较丁山地高,其主要原因是甲山地A.海拔较高
- 《圣经》中“马太福音”第25章有这么几句话:“凡有的,还要加给他,叫他多余;没有的,连他们所有的,也要夺过来。”1973
- 两人用同一标准盐酸滴定同一瓶NaOH溶液,甲将锥形瓶用NaOH待测液润洗后,使用水洗过的移液管移取碱液于锥形瓶中。乙用甲
- Suppose you are thinking aboutattending college in the Unite
- 北京市中心(天安门广场一带)的建筑物平均高度约35m,上海市中45(外滩一陆家嘴一带)的建筑物平均高度约75m。造成这一
- 2010年广州亚运会,我国选手郑幸娟以背越式成功地跳过1.90m高度,如图所示.下列有关郑幸娟跳高的说法正确的是 A.跨
- 2003年1月16日,北京市民李起在北京召开人大会期间,给人大代表写了一份谈对某项政策的信,到人大代表所住宾馆交信,既没
- 下列变化属于化学变化的是() A. 蜡烛燃烧 B. 冰雪融化 C. 汽油挥发 D.
- 如图所示是王洪同学连接的“电流跟电压关系”实验的电路图,各器件和连接都良好,闭合开关S后,可能出现的现象是(
- I don’t think ___ possible to master a foreign language with
- 一定温度下的密闭容器中发生可逆反应C(s) + H2O(g)CO(g) + H2(g),一定能说明该反应已达到平衡状态的
- 2015年8月12日,天津滨海新区某公司仓库发生爆炸,事发仓库里存放了大量的硝酸铵 (NH4NO3)、氰化钠(NaCN)
- His strength had almost when they found him in the des
- 国内网站纷纷开设“两会直通车”“网上大会堂”等论坛,网民热论国是。这表明 ①网络有利于政府了解社情民意,促进决策科学化和



