九年级(初三)数学下学期下册试题
已知:如图△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).

-
(1) 以点B 为位似中心,在网格内画出△A1BC1使△A1BC1与△ABC位似,且相似比为2:1,点C1的坐标是;
-
(2) △A1BC1的面积是平方单位.
下列图形的主视图与左视图不相同的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列四个几何体中,主视图是三角形的是( )
A .  B .
B .  C .
C .  D .
D . 
 D .
D . 
如图,点P(3a,a)是反比例函y= (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为
 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为 
学校教学楼前面有一根高是4.2米的旗杆,在某时刻太阳光下的影子长是6.3米,与此同时, 在旗杆周边的一棵大树在地面上投影出的影子长是9米,则此大树的高度是( )
A . 4.8米
B . 8.4米
C . 6米
D . 9米
若一个几何体的表面展开图如图所示,则这个几何体是( )

A . 三棱柱
B . 四棱柱
C . 三棱锥
D . 四棱锥
如图,过原点的直线与反比例函数  的图象交于
的图象交于  、
、  两点,点
两点,点  在第一象限,点
在第一象限,点  在
在  轴正半轴上,连接
轴正半轴上,连接  交反比例函数图象于点
交反比例函数图象于点  ,
,  为
为  的平分线,过点
的平分线,过点  作
作  的垂线,垂足为
的垂线,垂足为  ,连接
,连接  ,若
,若  ,
, 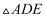 的面积为8,则
的面积为8,则  的值为( )
的值为( )
 的图象交于
的图象交于  、
、  两点,点
两点,点  在第一象限,点
在第一象限,点  在
在  轴正半轴上,连接
轴正半轴上,连接  交反比例函数图象于点
交反比例函数图象于点  ,
,  为
为  的平分线,过点
的平分线,过点  作
作  的垂线,垂足为
的垂线,垂足为  ,连接
,连接  ,若
,若  ,
, 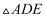 的面积为8,则
的面积为8,则  的值为( )
的值为( )

A . 4
B . 6
C . 8
D . 10
如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙EF上.

-
(1) 请你在墙上画出表示CD的部分影子EH;
-
(2) 若量得CE=1.2米,EH=1.5米,求立柱CD的高.
下列几何体中,其主视图、左视图和俯视图完全相同的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知变量y与x成反比,当x=1时,y=﹣6,则当y=3时,x=.
已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面圆的半径为cm.
如图,矩形ABCD中,点E在边DC上,且AD=8,AB=AE=17,那么tan∠AEB=.

如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于( )

A . 1:8
B . 1:2
C . 1:9
D . 1:3
如图,AB是⊙O的直径,BC交⊙O于点D,E是  的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB. 
-
(1) 求证:AC是⊙O的切线;
-
(2) 已知CD=4,CA=6,
①求CB的长;
②求DF的长.
如图所示是一个正方体纸盒的展开图,若在其中三个正方形的  内分别填入适当的数,使得它们折成正方体后
内分别填入适当的数,使得它们折成正方体后  与其相对面上的数互为相反数,
与其相对面上的数互为相反数,  与其相对面上的数互为倒数,则
与其相对面上的数互为倒数,则  ,
,  .
.
 内分别填入适当的数,使得它们折成正方体后
内分别填入适当的数,使得它们折成正方体后  与其相对面上的数互为相反数,
与其相对面上的数互为相反数,  与其相对面上的数互为倒数,则
与其相对面上的数互为倒数,则  ,
,  .
. 
如图所示,已知:点  ,点
,点  ,点
,点  ,在
,在  内依次作等边三角形,使一边在
内依次作等边三角形,使一边在  轴上,另一个顶点在
轴上,另一个顶点在  边上,作出的等边三角形分别是第
边上,作出的等边三角形分别是第  个
个  ,第
,第  个
个  ,第
,第  个
个  ,
,  ,则第
,则第  个等边三角形的边长等于 .
个等边三角形的边长等于 .
 ,点
,点  ,点
,点  ,在
,在  内依次作等边三角形,使一边在
内依次作等边三角形,使一边在  轴上,另一个顶点在
轴上,另一个顶点在  边上,作出的等边三角形分别是第
边上,作出的等边三角形分别是第  个
个  ,第
,第  个
个  ,第
,第  个
个  ,
,  ,则第
,则第  个等边三角形的边长等于 .
个等边三角形的边长等于 .
抛物线 过点A(-3,0),点B(1,0)与y轴交于点C,顶点为D,点E在y轴负半轴上.
过点A(-3,0),点B(1,0)与y轴交于点C,顶点为D,点E在y轴负半轴上.
 过点A(-3,0),点B(1,0)与y轴交于点C,顶点为D,点E在y轴负半轴上.
过点A(-3,0),点B(1,0)与y轴交于点C,顶点为D,点E在y轴负半轴上.
-
(1) 求抛物线的表达式及点D的坐标;
-
(2) 若△ADE是直角三角形,求点E的坐标;
-
(3) 点P是抛物线在第一象限内的点,连接AP交y轴于点H,连接AE交抛物线于点F,点G在线段OA上,且AG=CE,连接GH,若∠EAO=2∠OGH,
 , 求点F的坐标.
, 求点F的坐标.
一个长方形各边按  扩大后,得到的图形与原图形比较,下列说法中正确的是( )
扩大后,得到的图形与原图形比较,下列说法中正确的是( )
 扩大后,得到的图形与原图形比较,下列说法中正确的是( )
扩大后,得到的图形与原图形比较,下列说法中正确的是( )
A . 周长扩大原来的16倍
B . 周长缩小原来的 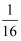 C . 面积扩大原来的16倍
D . 面积缩小原来的
C . 面积扩大原来的16倍
D . 面积缩小原来的 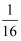
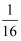 C . 面积扩大原来的16倍
D . 面积缩小原来的
C . 面积扩大原来的16倍
D . 面积缩小原来的 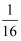
中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,AB是⊙O的直径,AC是弦,AC=3,∠BOC=2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是.

最近更新
- 朱熹曰:“方其知之而行未及之,则知尚浅。既亲历其域,则知之益明,非前日之意味。”下列观点蕴含的哲理与之相符的是: ①青山
- 下图中甲为海口、乙为南京、丙为北京、丁为哈尔滨四城市气温年变化曲线图。四地的气候特征和变化说明A.矛盾具有特殊性;事物是
- 某烃的结构简式为:,分子中含有四面体结构的碳原子数为a,在同一直线上的碳原子数最多为b,一定在同一平面内的碳原子数为c,
- 《十二铜表法》规定:“期满,债务人不还债的,债权人得拘捕之,押其到长官前,申请执行”;“禁止贵族与平民通婚”。由此可知《
- 党的十八届三中全会提出,建设社会主义文化强国,增强国家文化软实力,必须坚持社会主义先进文化前进方向,坚持中国特色社会主义
- 如图所示的四种情景,属于光的反射现象的是() A.叉鱼 B.手影 C.看到地上的书 D.凸透镜使光线会聚
- 某光电管的阴极是用金属钾制成的,它的逸出功为2.21 ev,用波长为2.5×10-7 m的紫外线照射阴极,已知真空中光速
- 将一盆栽植物横放于地,则其水平方向的主根近地一侧生长素浓度变化的曲线为(图中虚线表示对根生长既不促进也不抑制的生长素浓度
- 世界上人口,粮食,环境三大问题最突出的是 ( ) A.东亚
- 绿原酸的结构简式如图,下列有关绿原酸的说法错误的是()A.分子式为C16H18O9
- 根据短文内容,从短文后的选项中选出能填入空白处的最佳选项,选项中有两项为多余选项 The United States h
- BeforeDiana went abroad, she learned to do some _________ Ch
- 向50 g FeCl3的溶液中加入一小块钠,待反应完全后,过滤,得到仍有棕黄色的溶液45.9 g,则投入钠的质量为(
- 如图所示,将凸透镜固定在光具座上某位置(图中未标出),点燃的蜡烛放在光具座上的a点,调节光屏的位置,在光屏上得到烛焰清晰
- 张、李两家因承包鱼塘发生纠纷诉至法院。张家对法院一审不服,他可以( ) A.上诉
- 下列有关金属腐蚀与保护的说法正确的是 A. 常温下,断开K时,若M溶液为浓硫酸,则铁发生化学腐蚀 B. 关闭K,若M为氯
- The cause of his death __ his careless driving after too muc
- The Science Museum, _____ we visited during a recent trip to
- We dislike people______ talk much but never do anything. A.
- The dog _______for two months. Its _____made us very sad. A.



