九年级(初三)数学下学期下册试题
小宸想利用测量知识测算湖中小山的高度.他站在湖边看台上,清晰地看到小山倒映在平静的湖水中,如图所示,他在点O处测得小山顶端的仰角为45°,小山顶端A在水中倒影A′的俯角为60°.已知:点O到湖面的距离OD=3m,OD⊥DB,AB⊥DB,A、B、A′三点共线,A'B=AB,求小山的高度AB.(光线的折射忽略不计;结果保留根号)

如图,在直角坐标系中,直线  的图象上有8个点,从左往右依次记为
的图象上有8个点,从左往右依次记为  ,
,  ,…,
,…,  (横坐标依次增加2个单位),要使这些点平均分布在函数
(横坐标依次增加2个单位),要使这些点平均分布在函数  的图象两侧,每侧4个点,则
的图象两侧,每侧4个点,则  可以取到的整数值有( )
可以取到的整数值有( )
 的图象上有8个点,从左往右依次记为
的图象上有8个点,从左往右依次记为  ,
,  ,…,
,…,  (横坐标依次增加2个单位),要使这些点平均分布在函数
(横坐标依次增加2个单位),要使这些点平均分布在函数  的图象两侧,每侧4个点,则
的图象两侧,每侧4个点,则  可以取到的整数值有( )
可以取到的整数值有( ) 
A . 7个
B . 8个
C . 9个
D . 10个
如图,  和
和  是位似图形,点
是位似图形,点  是位似中心,点
是位似中心,点  ,
,  ,
,  分别是
分别是  ,
,  ,
, 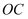 的中点.若
的中点.若  的面积为
的面积为  ,周长为
,周长为  ,则下列说法正确的是( )
,则下列说法正确的是( )
 和
和  是位似图形,点
是位似图形,点  是位似中心,点
是位似中心,点  ,
,  ,
,  分别是
分别是  ,
,  ,
, 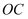 的中点.若
的中点.若  的面积为
的面积为  ,周长为
,周长为  ,则下列说法正确的是( )
,则下列说法正确的是( ) 
A .  的面积为
的面积为  B .
B .  的面积为
的面积为  C .
C .  的周长为
的周长为 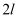 D .
D .  的周长为
的周长为 
 的面积为
的面积为  B .
B .  的面积为
的面积为  C .
C .  的周长为
的周长为 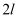 D .
D .  的周长为
的周长为 
圆锥的底面半径为4cm,高为5cm,则它的表面积为( )
A . 12πcm2
B . 26πcm2
C .  πcm2
D . (4
πcm2
D . (4  +16)πcm2
+16)πcm2
 πcm2
D . (4
πcm2
D . (4  +16)πcm2
+16)πcm2
反比例函数 的图象在每个象限内,y随x的增大而减小,则k的值可为( )
的图象在每个象限内,y随x的增大而减小,则k的值可为( )
 的图象在每个象限内,y随x的增大而减小,则k的值可为( )
的图象在每个象限内,y随x的增大而减小,则k的值可为( )
A . -1
B . 0
C . 1
D . 2
在  中,
中,  ,
,  ,则下列等式正确的是( )
,则下列等式正确的是( )
 中,
中,  ,
,  ,则下列等式正确的是( )
,则下列等式正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某小山坡的坡长为  米,山坡的高度为
米,山坡的高度为 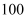 米,则该山坡的坡度
米,则该山坡的坡度 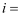 .
.
 米,山坡的高度为
米,山坡的高度为 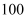 米,则该山坡的坡度
米,则该山坡的坡度 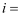 .
.
如图是由四个相同的小正方体组成的立体图形,它的左视图为( )

A . 
B .
B . 
C .
C . 
D .
D . 

B .
B . 
C .
C . 
D .
D . 
如图,平行于  的直线
的直线  把
把  分成面积相等的两部分,则
分成面积相等的两部分,则  .
.
 的直线
的直线  把
把  分成面积相等的两部分,则
分成面积相等的两部分,则  .
. 
如图1,抛物线与x轴相交于点A(  ,0),B(3,0),与y轴交于点C(0,3),点D是第一象限内抛物线上一动点,连接AC,BC.
,0),B(3,0),与y轴交于点C(0,3),点D是第一象限内抛物线上一动点,连接AC,BC.
 ,0),B(3,0),与y轴交于点C(0,3),点D是第一象限内抛物线上一动点,连接AC,BC.
,0),B(3,0),与y轴交于点C(0,3),点D是第一象限内抛物线上一动点,连接AC,BC.

-
(1) 求这条抛物线的解析式及顶点坐标;
-
(2) 过点D作DE⊥BC于点E,求线段DE的最大值;
-
(3) 如图2,若D为抛物线的顶点,连接BD,分别延长AC,BD交于点H,求tan∠CBH的值.
如图,已知直线  ,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若
,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若  ,
,  ,
,  ,则
,则  的值是( )
的值是( )
 ,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若
,直线m、n与a、b、c分别交于点A、C、E、B、D、F,若  ,
,  ,
,  ,则
,则  的值是( )
的值是( ) 
A . 15
B . 10
C . 14
D . 9
如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)

如图,在四边形  中,
中,  ,
,  ,
,  ,
,  ,点
,点  和点
和点  分别是
分别是  和
和  的中点,连接
的中点,连接  ,
,  ,
, 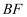 ,若
,若  ,则
,则  的面积是.
的面积是.
 中,
中,  ,
,  ,
,  ,
,  ,点
,点  和点
和点  分别是
分别是  和
和  的中点,连接
的中点,连接  ,
,  ,
, 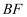 ,若
,若  ,则
,则  的面积是.
的面积是. 
如图,有一块三角形余料  ,
,  ,高线
,高线  ,要把它加工成一个矩形零件,使矩形的一边在
,要把它加工成一个矩形零件,使矩形的一边在  上,点
上,点  ,
,  分别在
分别在  ,
,  上,若满足
上,若满足  ,则
,则  的长为.
的长为.
 ,
,  ,高线
,高线  ,要把它加工成一个矩形零件,使矩形的一边在
,要把它加工成一个矩形零件,使矩形的一边在  上,点
上,点  ,
,  分别在
分别在  ,
,  上,若满足
上,若满足  ,则
,则  的长为.
的长为. 
某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
-
(1) 请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
-
(2) 按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
如图,P是反比例函数y= 的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是.
的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是.
 的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是.
的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的比例系数是.

直线DE交△ABC中的AB于D点,交AC于E点,那么能推出DE∥BC的条件是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E,F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:  ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
知识背景,当a>0且x>0时,因为  ,所以
,所以  ,从而
,从而 
 ,所以
,所以  ,从而
,从而 
(当x= 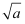 时取等号).
时取等号).
设函数y=x+  (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= 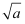 时,该函数有最小值为2
时,该函数有最小值为2 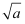 .
.
应用举例
已知函数为y1=x(x>0)与函数  (x>0),则当x=
(x>0),则当x=  =2时,y1+y2=x+
=2时,y1+y2=x+  有最小值为2
有最小值为2  =4.
=4.
解决问题
-
(1) 已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时,
 有最小值?最小值是多少?
有最小值?最小值是多少?
-
(2) 已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.
(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)

最近更新
- 下列反应在通常情况下可以发生:①2FeCl3+Cu====2FeCl2+CuCl2 ②Fe+CuSO4====FeSO4
- A few years after Mom died, Dad handed me a plastic bag. Tha
- 函数在下列哪个区间上为增函数 A. B. C. D.
- (2a+b)(2a-b)+b(2a+b)-4a2b÷b,其中a=-,b=2
- 呼吸运动的完成依赖于( ) A.肺泡的弹性 B.氧气和二氧化碳的交换 C.膈肌、肋间
- 阅读下面的小说,完成小题。 掀起帷幔 【美国】戴维·兰勃纳 从老板的办公室出来,看着乱七八糟的办公桌,我气得七窍生烟。已
- 欲鉴别一株高茎豌豆是否是纯合子,最简便易行的方法是( ) A.杂交 B.观察
- 下列有关说法中正确的是() A.20℃时,20g某固态物质能溶解在100g水中,所以20℃时该物质的溶解度为20g B.
- 根据因地制宜的发展原则,下列工业布局合理的是() A.在新疆建棉纺织加工厂 B.在湖南建甜菜加工厂 C.在黑龙江建
- 针对当前农村迷信盛行等状况,某市政府提出了充分发掘农村现有文化资源,在农村实施“创建特色文化村、创设农村文化室、举办农村
- 设A、B、C代表三种元素,已知:①A+和B-两种离子具有相同的电子层结构; ②C元素原子核内质子数比B元素原子核内质子数
- There_________ an important meeting tomorrow. A. will have
- 新修订的《环境空气质量标准》增加了PM2.5监测指标,PM2.5是指大气中直径小于或等于2.5微米的可吸入颗粒物。下列做
- 已知函数f(x)=.(1)当a>0时,解关于x的不等式f(x)<0;(2)若不等式f(x)≥f(1)对x∈R恒成立,求f
- 下列词语中,错别字最多的一项是 A.精萃 白内瘴 要言不繁 百尺杆头,更进一步 B.欠收 爆冷门 渊远流长
- 已知数列{an}的前n项和为Sn,an=5Sn-3(n∈N*),求(a1+a3+a5+…+a2n-1)的值.
- When his father came into the room, Paul stopped ________ ga
- 下列各项作为鉴定生物组织中还原糖的理想材料是( ) A.花生 B.番茄 C.胡萝卜 D.梨
- 先化简,再求值.,其中m=2.
- 下列水解的离子方程式正确的是 ( )A.NH4++H2ONH3·H2O+H+ B.Br-+H2O



