九年级(初三)数学下学期下册试题
如图1,已知A,B两点分别在x轴和y轴的正半轴上,连接AB与反比例函数  的图象交于C、D两点.
的图象交于C、D两点.
 的图象交于C、D两点.
的图象交于C、D两点. 
-
(1) 当OA=6,OB=3,点D的横坐标为2时,则k=,
 =.
=.
-
(2) 当OA=a,OB=b时,请猜测AC与BD之间的数量关系,并说明理由.
-
(3) 如图2,以D为顶点且过点O的抛物线分别交函数
 的图像和
的图像和  轴于点E、F,连接CF,设
轴于点E、F,连接CF,设  .
. ①若∠AFC=90°,则
 的值为多少?
的值为多少?②若∠ACF=90°,且
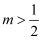 时,请用含
时,请用含  的代数式表示tan∠BAO的值.
的代数式表示tan∠BAO的值.
如图,EF表示一座风景秀美的观景山,AC,CE是已经修好的登山步行道。该景区为方便老年游客登顶观景,欲在山脚A与山顶E之间架设一条登山索道AE。在山脚A处测得点C的仰角为24°,在C处测得山顶E的仰角为45°,在山脚A处测得山顶E的仰角为37°.已知步行道AC长640米,则新架设的索道AE长多少米?
(参考数据:sin24°≈  ,cos 24°≈
,cos 24°≈ 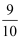 ,tan24°≈
,tan24°≈ 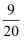 ,sin37°≈
,sin37°≈  ,cos37°≈
,cos37°≈  ,tan 37°≈
,tan 37°≈  )
)

 的值等于( )
的值等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为( )
A . 
B .
B . 
C .
C .  D .
D . 

B .
B . 
C .
C .  D .
D . 
如图,某校教学楼  与实验楼
与实验楼  的水平间距
的水平间距  米,在实验楼顶部
米,在实验楼顶部  点测得教学楼顶部
点测得教学楼顶部  点的仰角是
点的仰角是  ,底部
,底部  点的俯角是
点的俯角是  ,则教学楼
,则教学楼  的高度是米(结果保留根号).
的高度是米(结果保留根号).

 与实验楼
与实验楼  的水平间距
的水平间距  米,在实验楼顶部
米,在实验楼顶部  点测得教学楼顶部
点测得教学楼顶部  点的仰角是
点的仰角是  ,底部
,底部  点的俯角是
点的俯角是  ,则教学楼
,则教学楼  的高度是米(结果保留根号).
的高度是米(结果保留根号).
如图,四边形ABCD∽四边形EFGH,连接相应的对角线AC,EG.

-
(1) 求证△ABC∽△EFG;
-
(2) 若
 =
=  ,直接写出四边形ABCD与四边形EFGH的面积比为.
,直接写出四边形ABCD与四边形EFGH的面积比为.
如图,△P1OA1 , △P2A1A2都是等腰直角三角形,点P1 , P2都在函数y=  (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
 (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( ) 
A . (4  ,
,  )
B . (4+2
)
B . (4+2  ,4﹣2
,4﹣2  )
C . (2+2
)
C . (2+2  ,2
,2  ﹣2)
D . (4+2
﹣2)
D . (4+2  ,2+2
,2+2  )
)
 ,
,  )
B . (4+2
)
B . (4+2  ,4﹣2
,4﹣2  )
C . (2+2
)
C . (2+2  ,2
,2  ﹣2)
D . (4+2
﹣2)
D . (4+2  ,2+2
,2+2  )
)
由若干个完全相同的小立方块搭成的几何体的左视图和俯视图如图所示,则搭成该几何体所用的小立方块的个数可能是( )

A . 4个
B . 5个
C . 7个
D . 8个
如图是一个几何体的俯视图,则该几何体是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C . 
一个正方体的表面展开图如图所示,则与“你”字相对的面是( )

A . 心
B . 想
C . 事
D . 成
如图,某同学用圆规  画一个半径为
画一个半径为 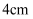 的圆,测得此时
的圆,测得此时  ,为了画一个半径更大的同心圆,固定
,为了画一个半径更大的同心圆,固定  端不动,将
端不动,将  端向左移至
端向左移至 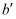 处,此时测得
处,此时测得  ,则
,则  的长为( )
的长为( )
 画一个半径为
画一个半径为 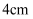 的圆,测得此时
的圆,测得此时  ,为了画一个半径更大的同心圆,固定
,为了画一个半径更大的同心圆,固定  端不动,将
端不动,将  端向左移至
端向左移至 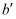 处,此时测得
处,此时测得  ,则
,则  的长为( )
的长为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
图是由四个完全相同的正方体组成的几何体,这个几何体的左视图是 ( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一次课外实践活动中,一个小组利用热气球的探测器测量一栋楼房的高度如图所示,热气球的探测器显示,从热气球看这栋楼楼顶的仰角为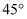 , 看这栋楼底部的俯角为
, 看这栋楼底部的俯角为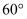 , 热气球与楼的水平距离为100米,求这栋楼的高度(结果保留整数,参考数据:
, 热气球与楼的水平距离为100米,求这栋楼的高度(结果保留整数,参考数据: ,
,  ).
).
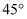 , 看这栋楼底部的俯角为
, 看这栋楼底部的俯角为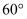 , 热气球与楼的水平距离为100米,求这栋楼的高度(结果保留整数,参考数据:
, 热气球与楼的水平距离为100米,求这栋楼的高度(结果保留整数,参考数据: ,
,  ).
).
如图,菱形ABCD的两个顶点B,D在反比例函数  的图像上,对角线AC与BD的交点恰好是坐标原点0,已知点A(2,2),∠BAC=60°,则k的值是.
的图像上,对角线AC与BD的交点恰好是坐标原点0,已知点A(2,2),∠BAC=60°,则k的值是.
 的图像上,对角线AC与BD的交点恰好是坐标原点0,已知点A(2,2),∠BAC=60°,则k的值是.
的图像上,对角线AC与BD的交点恰好是坐标原点0,已知点A(2,2),∠BAC=60°,则k的值是. 
上海与杭州的实际距离约200千米,在比例尺为1:5000000的地图上,上海与杭州的图上距离约 厘米.
水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.

先化简,再求值:  ,其中a=(
,其中a=(  )-1-
)-1- 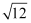 +(π-3.14)0+2cos30°
+(π-3.14)0+2cos30°
 ,其中a=(
,其中a=(  )-1-
)-1- 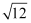 +(π-3.14)0+2cos30°
+(π-3.14)0+2cos30°
两个相似三角形面积比是9:25,其中较小一个三角形的周长为18cm,则另一个三角形的周长是cm.
如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,则tanA的值为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
将三角形纸片(  )按如图所示的方式折叠,使点
)按如图所示的方式折叠,使点  落在边
落在边  上,记为点
上,记为点 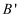 ,折痕为
,折痕为  ,已知
,已知  ,
,  ,若以点
,若以点 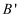 ,
,  ,
,  为顶点的三角形与
为顶点的三角形与  相似,则
相似,则 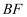 的长度是.
的长度是.
 )按如图所示的方式折叠,使点
)按如图所示的方式折叠,使点  落在边
落在边  上,记为点
上,记为点 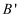 ,折痕为
,折痕为  ,已知
,已知  ,
,  ,若以点
,若以点 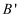 ,
,  ,
,  为顶点的三角形与
为顶点的三角形与  相似,则
相似,则 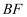 的长度是.
的长度是. 
最近更新
- 《中国党内法规制定条例》和《中国党内法规和规范性文件备案规定》出台,自此中国首次拥有了正式的党内“立法法”。这体现了中国
- 干旱灾害是中国主要的气象灾害之一。下图反映了我国1950-1991年间不同区域季节分布及其对农业的影响,读图回答下列问题
- 如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=a(0<≦1
- If US software(软件) companies don’t pay more attention to qua
- 将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为.
- 人类祖先与猿分界的重要标志是( ) A.会使用天然工具
- 用下图装置测定种子萌发时进行的呼吸作用类型,同时关闭活塞,在25 ℃下经过20 min再观察红色液滴移动情况,下列对实验
- 碱基互补配对发生在下列哪些生理过程或生物技术中: ( ) ①种子的萌发 ②病毒的增殖过程
- 贾复字君文,南阳冠军人也。少好学,习《尚书》。事舞阴李生,李生奇之,谓门人曰:“贾君之容貌志气如此,而勤于学,将相之器也
- 空气吹出法是目前海水提溴的最主要方法之一。其工艺流程如图所示:(1)步骤④利用了SO2的还原性,反应的离子方程式为 __
- 《论语·颜渊》曰“颜渊问仁,子曰,克己复礼为仁,一曰克已复礼,天下归仁焉。”有人对这段话的解释是:“仁者,本心之全德。克
- 下列有关电化学的示意图中正确的是() A. B. C. D.
- 在一宗交通事故中,某人大脑受伤,不能说话但能听懂别人的说话,不能写字但能看书看报,那么受损的部位是()
- Becausehe was _______ the new limit,he was stopped and warn
- 以下说法正确的是( )A.纳米材料是指一种称为“纳米”的新物质制成的材料B.绿色食品是指不含任何化学物质的食品C.
- Authorities in Shanghai said Thursday night that anotherpers
- 等于A. B. C. D.
- 1mol某烃完全燃烧可得到2mol CO2,在一定条件下,1mol该烃能与2mol H2发生加成反应,这种烃是(
- 倘若自然界的细菌、真菌等突然消失,则将会出现:A.动植物大量繁殖 B.人类没有传染病 C.植物没有病虫害
- 许挺说,以前古孝称“父母在,不远游”但现在为了求学、为了事业,许多年轻人都不得不离开父母到别的城市去发展,但这并不意味着



