九年级(初三)数学下学期下册试题
计算:2cos230°﹣2sin60°×cos45°.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.

-
(1) 求证:CB∥PD;
-
(2) 若BC=6,sin∠P=
 ,求AB的值.
,求AB的值.
已知一个正多边形的一个外角的余弦值为  ,那么它是边形.
,那么它是边形.
 ,那么它是边形.
,那么它是边形.
如图,在△ABC中,∠C=90°,AB=10,cosB=  ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是.
 ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是. 
坡度等于1: 的斜坡的坡角等于( )
的斜坡的坡角等于( )
 的斜坡的坡角等于( )
的斜坡的坡角等于( )
A . 30°
B . 40°
C . 50°
D . 60°
如图所示的几何体,它的左视图正确的是( )

A .  B .
B .  C .
C .  D .
D . 
当三角形的面积为12cm2时,它的底边a(cm)与底边上的高h(cm)之间的函数关系式为 .
如图,已知AB∥CD∥EF , AD:AF=3:5,BE=12,那么CE的长等于( )

A .  B .
B .  C .
C . 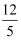 D .
D . 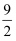
 B .
B .  C .
C . 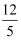 D .
D . 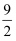
用小立方块搭一个几何体,使它从正面和从上面看的形状图如图所示.从上面看的形状图中,小方形中的字母表示该位置小立方块的个数,试回答下列问题.

-
(1) x,z各表示多少?
-
(2) y可能是多少?这个几何体最少由几个小立方块搭成?最多呢?
如图,有反比例函数  ,
,  的图象和一个圆,则图中阴影部分的面积是( )
的图象和一个圆,则图中阴影部分的面积是( )

A . π
B . 2π
C . 4π
D . 条件不足,无法求
为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了依次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表:
各组人数统计表
组号 | 年龄分组 | 频数(人) | 频率 |
第一组 | 20≤x<25 | 50 | 0.05 |
第二组 | 25≤x<30 | a | 0.35 |
第三组 | 35≤x<35 | 300 | 0.3 |
第四组 | 35≤x<40 | 200 | b |
第五组 | 40≤x≤45 | 100 | 0.1 |

-
(1) 求本次调查的样本容量及表中的a、b的值;
-
(2) 调查结果得到对生产和居住环境满意的人数的频率分布直方图如图,政策规定:本次调查满意人数超过调查人数的一半,则称调查结果为满意.如果第一组满意人数为36,请问此次调查结果是否满意;并指出第五组满意人数的百分比;
-
(3) 从第二张和第四组对生产和居住环境满意的职工中分别抽取3人和2人作义务宣传员,在这5人中随机抽取2人介绍经验,求第二组和第四组恰好各有1人被抽中介绍经验的概率.
已知:x=2sin60°,先化简 +
+ ,再求它的值.
,再求它的值.
 +
+ ,再求它的值.
,再求它的值.
在某一电路中,保持电压不变,电流I(单位:A)与电阻R(单位:Ω)成反比例,当电阻R=5Ω时,电流I=2A.
-
(1) 求I与R之间的函数关系式;
-
(2) 当电流为20A时,电阻应是多少?
如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣  的图象交于点A(m,4),则这个二次函数的解析式为( )
的图象交于点A(m,4),则这个二次函数的解析式为( )
 的图象交于点A(m,4),则这个二次函数的解析式为( )
的图象交于点A(m,4),则这个二次函数的解析式为( )

A . y=x2﹣x﹣2
B . y=x2﹣x+2
C . y=x2+x﹣2
D . y=x2+x+2
-
(1) 计算:3tan30°-

-
(2) 化简:

将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )

A . 考
B . 试
C . 成
D . 功
阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”:如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:

-
(1) 如图1,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
-
(2) 如图2,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
-
(3) 如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
“跳眼法”是指用手指和眼睛估测距离的方法
步骤:
第一步:水平举起右臂,大拇指紧直向上,大臂与身体垂直;
第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;
第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离的长度;
第四步:将横向距离乘以10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测,点的距离值.
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图,该汽车的长度大约为4米,则汽车到观测点的距离约为( )

A . 40米
B . 60米
C . 80米
D . 100米
若点  在反比例函数
在反比例函数  的图象上,则
的图象上,则  的大小关系是( )
的大小关系是( )
 在反比例函数
在反比例函数  的图象上,则
的图象上,则  的大小关系是( )
的大小关系是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知△A′B′C′与△ABC是位似图形,点O是位似中心,若A′是OA的中点,则△A′B'C′与△ABC的面积比是( )

A . 1:4
B . 1:2
C . 2:1
D . 4:1
最近更新
- 若展开式中含项的系数与含项的系数之比为-5,则n等于 ( ) A.4
- 下列句子中,没有语病的一句是 A记者近日发现,公园晨练的老年人中流行一种由松树精华做成的“神仙茶”,对这种带点儿树皮味的
- 鸡蛋壳的主要成分是碳酸钙,将一个新鲜的鸡蛋放在盛有足量稀盐酸的玻璃杯中,可以观察到鸡蛋冒气泡,该气泡的主要成分是(
- 唐太宗、武则天、唐玄宗都共同注意的问题是( ) A.轻徭薄赋 B
- 已知关于x的一元二次方程x2+kx+1=0有两个相等的实数根,则k=_______.
- 热量----分别串联和并联----所用的时间两根阻值相同的电阻丝,分别串联和并联后接在同一电源上,烧开壶水所用的时间分别
- He ______ in his garden every morning next year. A. will wo
- 从1915年起,陈独秀、李大钊、鲁迅等激进的民主主义者以《新青年》为主要阵地,掀起了新文化运动。他们在新文化运动中高举的
- 阅读下面的文言文,后面题目。(9分,每小题3分) 项王已约,乃引兵解而东归。 汉欲西归,张良、陈平说曰:“汉有天下太半,
- (本题3分+3分+4分)如图,已知二次函数的图象与x轴交于A、B两点,与y轴交于点P,顶点为C()。(1)求此函数的关系
- 下列反应中,属于加成反应的是( )。 A.SO3+H2O=H2SO4
- 观察下列图表.指出1895——1900年我国出现这种经济状况的主要原因是( )A.清政府放宽了对设厂的限制
- 图9为上海市工业用地分布示意图。读图完成16一17题。 16.图示工业基地和工业园区分布状况的主导区位条件是
- 双曲线的渐近线方程是( ) A、 B、 C、 D、
- 某溶液中,若忽略水的电离,只含有下表中所示的四种离子,试推测X 离子及其个数b可能为 ( )离子 Na+ Al3
- 钱乘旦先生在《不平衡发展:20世纪历史与现代化》一文中称:“西方现代化经几百年的发展,其优与弊都已经十分清楚。二战后企图
- 下列几何体的三视图中,左视图是圆的是A.① B.② C.③
- 制作泡菜时要用特殊的坛子,坛子口必须加水密封,其目的是() A.隔绝空气,抑制细菌繁殖 B.阻止尘埃、细菌入坛,防止污染
- ______ the question made her teacher angry and upset. A. J
- 党的十七大报告强调:制定与群众利益密切相关的法律法规和公共政策原则上都要 公开听取意见。这主要是因为( ) A.决策是公



