九年级(初三)数学下学期下册试题
如图,反比例函数  的图象经过点
的图象经过点  ,直线
,直线  与双曲线交于另一点
与双曲线交于另一点  ,作
,作  轴于点
轴于点  ,
,  轴于点
轴于点  ,连接
,连接  .
.
 的图象经过点
的图象经过点  ,直线
,直线  与双曲线交于另一点
与双曲线交于另一点  ,作
,作  轴于点
轴于点  ,
,  轴于点
轴于点  ,连接
,连接  .
. 
-
(1) 求
 的值;
的值;
-
(2) 若
 ,求直线
,求直线  的解析式;
的解析式;
-
(3) 若
 ,其它条件不变,直接写出
,其它条件不变,直接写出  与
与  的位置关系.
的位置关系.
如图,△ABC中,∠B=60,∠ACB=75,点D是BC边上一动点,以AD为直径作⊙O , 分别交AB、AC于E、F , 若弦EF的最小值为1,则AB的长为

A .  B .
B .  C . 1.5
D .
C . 1.5
D . 

如图,  是等边三角形,中线
是等边三角形,中线  ,
, 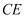 交于点
交于点  ,
,  ,则
,则  的长为.
的长为.
 是等边三角形,中线
是等边三角形,中线  ,
, 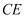 交于点
交于点  ,
,  ,则
,则  的长为.
的长为. 
某几何体的三视图如图所示,则下列说法错误的是( )

A . 该几何体是长方体
B . 该几何体的高是3
C . 底面有一边的长是1
D . 该几何体的表面积为18平方单位
如图,在平面直角坐标系中,0为坐标原点,点A、B分别为直线y=-  x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC.
x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC.
 x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC.
x+6与x轴、y轴的交点.动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的交点分别为C、D,连接CD、QC. 
-
(1) 求当t为何值时,点Q与点D重合?
-
(2) 设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
-
(3) 若⊙P与线段QC只有一个交点,请直接写出t的取值范围.
某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示, 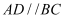 ),村委会想在
),村委会想在  地带与
地带与  地带种植单价为10元的太阳花,当
地带种植单价为10元的太阳花,当  地带种满花后,已经花了500元,请你计算一下,若继续在
地带种满花后,已经花了500元,请你计算一下,若继续在  地带种植同样的太阳花,资金是否够用?并说明理由.
地带种植同样的太阳花,资金是否够用?并说明理由.
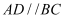 ),村委会想在
),村委会想在  地带与
地带与  地带种植单价为10元的太阳花,当
地带种植单价为10元的太阳花,当  地带种满花后,已经花了500元,请你计算一下,若继续在
地带种满花后,已经花了500元,请你计算一下,若继续在  地带种植同样的太阳花,资金是否够用?并说明理由.
地带种植同样的太阳花,资金是否够用?并说明理由. 
如图,已知点E是矩形 的对角线
的对角线 上的一动点,正方形
上的一动点,正方形 的顶点
的顶点 都在边
都在边 上,若
上,若 , 则
, 则 .
.
 的对角线
的对角线 上的一动点,正方形
上的一动点,正方形 的顶点
的顶点 都在边
都在边 上,若
上,若 , 则
, 则 .
.
下列4个平面图形中,能够围成圆柱侧面的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算  .
.
 .
.
若一个几何体的三视图都是正方形,则这个几何体是( )
A . 长方体
B . 正方体
C . 圆柱
D . 圆锥
“地球一小时“是世界自然基金会应对全球气候变化所提出的一项全球性节能活动,提倡于每年三月最后一个星期六的当地时间晚上 20:30(2019 年“地球一小时”时间为 3 月20日晚上 20:30),家庭及商界用户关上不必要的电灯及耗电产品一小时,以此增强群众环境保护的意识,小明也参加了这次活动,为了解居民用电情况,小明调查了部分同学某月的家庭用电量,根据调查数据制作了频数分布直方图和扇形统计图,第21题图1中从左到右各长方形的高度之比为2:8:9:7:3:1.

-
(1) 已知用电量60≤x<80(度/月)的家庭有12个,则此次行动共调查了家庭;
-
(2) 在第21题图2中,用电量20≤x<40(度/月)部分的圆心角为度;
-
(3) 小明把第21题图1中用电量20≤x<30的都看成25,用电量30≤x<40都看成35,以此类推,若小明学校的同学来自1200个家庭,则按小明的方法,可估算用电量x≥50(度/月)的家庭一个月的用电量约为多少度?
如图,在平面直角坐标系xOy中,已知菱形ABCD的顶点A(0,2  )和C(2,0),顶点B在x轴上,顶点D在反比例函数y=
)和C(2,0),顶点B在x轴上,顶点D在反比例函数y=  的图象上,点E为边CD上的动点,过点E作EF∥x轴交反比例函数图象于点F,过点F作FG∥CD交x轴于点G,当CE=CG时,点F的坐标为.
的图象上,点E为边CD上的动点,过点E作EF∥x轴交反比例函数图象于点F,过点F作FG∥CD交x轴于点G,当CE=CG时,点F的坐标为.
 )和C(2,0),顶点B在x轴上,顶点D在反比例函数y=
)和C(2,0),顶点B在x轴上,顶点D在反比例函数y=  的图象上,点E为边CD上的动点,过点E作EF∥x轴交反比例函数图象于点F,过点F作FG∥CD交x轴于点G,当CE=CG时,点F的坐标为.
的图象上,点E为边CD上的动点,过点E作EF∥x轴交反比例函数图象于点F,过点F作FG∥CD交x轴于点G,当CE=CG时,点F的坐标为. 
如图,四边形ABCd为边长是2的正方形,△BPC为等边三角形,连接PD、BD,则△BDP的面积是.

下列各点落在反比例函数y= 图象上的是( )
图象上的是( )
 图象上的是( )
图象上的是( )
A . (-4,1)
B . (-1,4)
C . (2,2)
D . (-2,2)
在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y=  的图象交于点A(m,4).
的图象交于点A(m,4).
 的图象交于点A(m,4).
的图象交于点A(m,4).
-
(1) 求正比例函数的解析式;
-
(2) 将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值.
已知反比例函数  的图象经过点(-1,-2).
的图象经过点(-1,-2).
 的图象经过点(-1,-2).
的图象经过点(-1,-2).
-
(1) 求y与x的函数关系式;
-
(2) 若点(2,n)在这个图象上,求n的值.
 =.
=.
如图,在△ABC中,已知DE∥BC,AD=2,BD=3,AE=1,则EC=.

已知一次函数  的图象与反比例函数
的图象与反比例函数  的图象交于点
的图象交于点  ,若
,若  =2,则反比例函数的表达式为.
=2,则反比例函数的表达式为.
 的图象与反比例函数
的图象与反比例函数  的图象交于点
的图象交于点  ,若
,若  =2,则反比例函数的表达式为.
=2,则反比例函数的表达式为.
点  ,
,  ,
,  ,
,  在反比例函数
在反比例函数 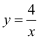 图象上,则
图象上,则  ,
,  ,
,  ,
,  中最小的是( )
中最小的是( )
 ,
,  ,
,  ,
,  在反比例函数
在反比例函数 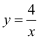 图象上,则
图象上,则  ,
,  ,
,  ,
,  中最小的是( )
中最小的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 新中国建立初期,刘少奇从中国实际出发,倡导的两种“教育制度”是指() ①全日制学校教育制度 ②半工半读学校教育制度 ③职
- 古希腊流传这样一个传奇故事:一批贩运纯碱的商船停泊在江边的沙岸上,商人们找不到石头来搭灶煮饭,就把船上的大块纯碱搬来,放
- 如图1,半径为R的水平圆盘正以中心O为转轴匀速转动(从上往下看,逆时针方向转动),从圆板中心O的正上方h高处水平抛出一球
- 如图,平行板电容器的两个极板与水平地面成一角度,两极板与一直流电源相连.若一带电粒子恰能沿图中所示水平直线通过电容器,则
- 如图所示,白炽灯和电容串联后接在交变电源的两端,当交变电源的频率增大时( ) A.电容器电容增加
- 同样是遵循社会发展的客观规律作出的价值判断和价值选择,我们党在不同历史阶段为自己确立的目标和完成的历史任务不同。这说明(
- 阅读下面这首唐诗,按要求作答。(11分) 望蓟门 祖 咏 燕台一去客心惊,笳鼓喧喧汉将营。万里寒光生积雪,三边曙色动危旌
- 1898年,袁世凯为慈禧贺寿,进贡一辆奔驰轿车。不料,太后仅坐一次便弃之不用了。原来,汽车解决不了“尊卑”问题,司机
- (08年华师一附中二次压轴文) 的展开式中常数项是 。
- 在离体的植物器官、组织或细胞脱分化形成愈伤组织过程中,下列哪一项是不需要的( ) A.消毒灭菌
- 巴黎公社是国际工人运动史上的伟大创举,主要表现在 A、废除了旧的军队、警察、法庭等,建立新的国家机构 B、规定工作人员
- 往含I-和Cl-的稀溶液中滴入AgNO3溶液,沉淀的质量与加入AgNO3溶液体积的关系如下图所示。则 原溶液中c(I-)
- A 公司拟巨资购入S 公司发行的股份,双方将在多领域进行深入合作,预计这一合作在未来三年内将给S 公司带来大约3.8 亿
- 电风扇扇叶作匀速圆周运动,每秒钟转25圈,则电风扇叶作匀速圆周运动的周期为 s,频率为 Hz
- 2010年2月5日,《沈阳日报》报道,沈阳市为了保证行政、司法机关公正执法和便于社会监督,实施了阳光工程——执法公示制,
- 阅读下面的文字,根据要求作文。 孩子,如果你去远方,你该先拥有什么呢? 请你联系实际进行思考,任选一个角度,自拟标题,写
- (08甘肃嘉峪关)阅读材料,回答问题: 专家告诉记者:“很多人以为不看电视、不开空调、不开电脑就不会耗电。事
- 有一种称为“摇头丸”的毒品已从国外流入我国某些城市,服用后会使人出现食欲减退、血压升高、飘飘然的幻觉等症状
- 历史学家评论1832年英国议会改革时说:“英国比欧洲任何国家也许更接近于革命。”因为 A.资产阶级和新贵族力量强大
- 下列事实与浓硫酸表现出的性质(括号中)对应关系正确的是( ) A、在空气中敞口久置的浓硫酸,溶液质量增大(难挥发性)



