九年级(初三)数学：上学期上册　　 下学期下册

九年级(初三)数学下学期下册试题

如图：在等腰△ABC中，∠C=90º，AC=6，D 是AC上一点，若tan∠DBA=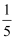 $\text{[math]}$ ，则AD的长为（）

A . $\text{[math]}$ B . 2 C . 1 D . $\text{[math]}$

一个几何体如图所示，它的左视图是（）

A .

B .

C .

D .

如上图所示．已知：在正方形ABCD中，∠BAC的平分线交BC于E，作EF⊥AC于F，作FG⊥AB于G．则 $\text{[math]}$ =．

如图，直线 $\text{[math]}$ 与⊙ $\text{[math]}$ 相切于点 $\text{[math]}$ 为⊙ $\text{[math]}$ 的直径， $\text{[math]}$ 是直径 $\text{[math]}$ 右侧半圆上的一个动点(不与点 $\text{[math]}$ 、 $\text{[math]}$ 重合)，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ .设 $\text{[math]}$ , $\text{[math]}$ .

图片_x0020_2120702286

求:

（1） $\text{[math]}$ 与 $\text{[math]}$ 相似吗?为什么?
（2）求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式;
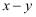（3）当 $\text{[math]}$ 为何值时， $\text{[math]}$ 取得最大值，最大值为多少?

已知△ABC∽△DEF，且相似比为3：4，S_△ABC=2cm² ，则S_△DEF=

对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y随x的增大而减小，则m的取值范围是.

如图，水杯的杯口与投影面平行，投影线的几方向如箭头所示，它的正投影是（）

图片_x0020_100006

A .

B .

C .

D .

画出下图几何体的3种形状图。

若反比例函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，则m=．

把如图的展开图还原成正方体，与数5相对面的数是（）

A . 1 B . 3 C . 4 D . 6

在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN（如图），在跑道MN的正西端14.5千米处有一观察站A．某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°，且与点A相距15千米的B处；经过1分钟，又测得该飞机位于点A的北偏东60°，且与点A相距5 $\text{[math]}$ 千米的C处．

（1）该飞机航行的速度是多少千米/小时？（结果保留根号）
（2）如果该飞机不改变航向继续航行，那么飞机能否降落在跑道MN之间？请说明理由．

如图，矩形OABC与矩形ODEF是位似图形，点O为位似中心，相似比为1：1.2，点B的坐标为（﹣3，2），则点E的坐标是（　　）

A . （3.6，2.4） B . （3，2.4） C . （﹣3，2.4） D . （﹣3.6，2.4）

如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是反比例函数 $\text{[math]}$ 在第一象限的图象上的点，它们的横坐标分别为2，4，6.过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别作 $\text{[math]}$ 轴， $\text{[math]}$ 轴的垂线段，构成多个矩形.若图中阴影部分的面积为12，则点 $\text{[math]}$ 的坐标为.

图片_x0020_100012

李老师为了准备网课直播，购买了一个三脚架，如图①所示，图②为其截面示意图．测得 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ．求点 $\text{[math]}$ 到地面 $\text{[math]}$ 的高度（结果精确到 $\text{[math]}$ ）．

（参考数据： $\text{[math]}$ ．）