九年级(初三)数学下学期下册试题
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.

下图是由相同小正方体组成的立体图形,它的主视图为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
矩形ABCD中,E为边AB上一点,将 沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若
沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若 ,
,  .
.
 沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若
沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若 ,
,  .
. 
-
(1) 矩形ABCD的面积为;
-
(2)
 的值为.
的值为.
如图,△ ∽△
∽△ , 若
, 若 ,
,  ,
,  , 则
, 则 的长是( )
的长是( )
 ∽△
∽△ , 若
, 若 ,
,  ,
,  , 则
, 则 的长是( )
的长是( )
A . 2
B . 3
C . 4
D . 5
下列几何体中,俯视图是三角形的几何体是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若等边三角形ABC的边长为  cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
 cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是.
如图,点P在反比例函数y=  (x<0)的图象上,过P分别作x轴、y轴的垂线,垂足分别为点A、B.已知矩形PAOB的面积为8,则k=.
(x<0)的图象上,过P分别作x轴、y轴的垂线,垂足分别为点A、B.已知矩形PAOB的面积为8,则k=.
 (x<0)的图象上,过P分别作x轴、y轴的垂线,垂足分别为点A、B.已知矩形PAOB的面积为8,则k=.
(x<0)的图象上,过P分别作x轴、y轴的垂线,垂足分别为点A、B.已知矩形PAOB的面积为8,则k=. 
如图所示的几何体从上面看到的图形是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D .
如图,抛物线  与x轴交于点
与x轴交于点  和
和  ,与y轴交于点C
,与y轴交于点C
 与x轴交于点
与x轴交于点  和
和  ,与y轴交于点C
,与y轴交于点C 
-
(1) 求抛物线的表达式;
-
(2) 如图1,若点F在线段OC上,且
 ,经入过点F的直线在第一象限内与抛物线交于点D,与线段BC交于点E,求
,经入过点F的直线在第一象限内与抛物线交于点D,与线段BC交于点E,求  的最大值;
的最大值;
-
(3) 如图2,若P为抛物线的顶点,动点Q在抛物线上,当
 时,请直接写出点Q的坐标.
时,请直接写出点Q的坐标.
在平面直角坐标系中,点A,B,C是x轴的正半轴上从左向右依次排列的三点,过点A,B,C分别作与  轴平行的直线
轴平行的直线  ,
,  ,
,  .
.
 轴平行的直线
轴平行的直线  ,
,  ,
,  .
.

-
(1) 如图1,若直线
 与直线
与直线  ,
,  ,
,  分别交于点D,E,F三点,设D(
分别交于点D,E,F三点,设D(  ,
,  ),E(
),E(  ,
,  ),F(
),F(  ,
,  ).
).
①若
 ,
,  ,
,  ,则
,则 
 (填“=”,“>”或“<”);
(填“=”,“>”或“<”);②若
 ,
,  ,
,  (
(  ),求证:AB=BC;
),求证:AB=BC; -
(2) 如图2,点A,B,C的横坐标分别为
 ,n,
,n,  (
(  ),直线
),直线  ,
,  ,
,  与反比例函数
与反比例函数  (
(  )的图像分别交于点D,E,F,根据以上探究的经验,探索
)的图像分别交于点D,E,F,根据以上探究的经验,探索
 与
与  之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
下面的三个图形是某几何体的三种视图,则该几何体是( )
A . 正方体
B . 圆柱体
C . 圆锥体
D . 球体
抛物线  与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
 与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C. 
-
(1) 如图1,若A(-1,0),B(3,0),
① 求抛物线
 的解析式;
的解析式;② P为抛物线上一点,连接AC,PC,若∠PCO=3∠ACO,求点P的横坐标;
-
(2) 如图2,D为x轴下方抛物线上一点,连DA,DB,若∠BDA+2∠BAD=90°,求点D的纵坐标.
某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,b)对应大鱼上的点( )

A . (-2a,2b)
B . (-2a,-2b)
C . (-2b,-2a)
D . (-2a,-b)
《攀登者》于2019年9月30日在中国内地上映.展现出了中国登山队为了国家使命勇于攀登的精神.在2021年4月30日,一支登山队再一次成功地登上了珠峰之巅,站上了珠峰顶部.已知一个人登山时的动作可以简化成下图所示,他的大腿长AB=AC=45cm,上坡时大腿之间的夹角∠BAC=65°,某段山坡DF的坡度为i= , 大约走多少步才能将自己所处位置的海拔提高50米?
, 大约走多少步才能将自己所处位置的海拔提高50米?
 , 大约走多少步才能将自己所处位置的海拔提高50米?
, 大约走多少步才能将自己所处位置的海拔提高50米?(结果保留两位小数,sin65°≈ , tan65°≈
, tan65°≈ , cos65°≈
, cos65°≈ )
)

如图,在  中,
中,  ,
,  ,
,  ,点
,点  是
是  中点,连结
中点,连结  .动点
.动点  从点
从点  出发沿折线
出发沿折线  方向以每秒2个单位长度的速度向终点
方向以每秒2个单位长度的速度向终点  运动,过点
运动,过点  作
作  ,垂足为点
,垂足为点  ,以
,以  ,
, 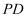 为邻边作平行四边形
为邻边作平行四边形  .设点
.设点  的运动时间为
的运动时间为  (秒).
(秒).
 中,
中,  ,
,  ,
,  ,点
,点  是
是  中点,连结
中点,连结  .动点
.动点  从点
从点  出发沿折线
出发沿折线  方向以每秒2个单位长度的速度向终点
方向以每秒2个单位长度的速度向终点  运动,过点
运动,过点  作
作  ,垂足为点
,垂足为点  ,以
,以  ,
, 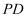 为邻边作平行四边形
为邻边作平行四边形  .设点
.设点  的运动时间为
的运动时间为  (秒).
(秒). 
-
(1) CD=.
-
(2) 当点
 在
在  上时,求
上时,求  的长度(用含
的长度(用含  的代数式表示)
的代数式表示)
-
(3) 当平行四边形
 与
与  重合部分图形的面积为
重合部分图形的面积为  时,求
时,求  与
与  之间的函数关系式.
之间的函数关系式.
-
(4) 当点
 落在
落在  的某个内角平分线上时请直接写出
的某个内角平分线上时请直接写出  的值.
的值.
sin30°的值为.
某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线.

-
(1) 请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法);
-
(2) 求小明到达点F时的影长FH的长.
如图,在△ABC中,DE∥BC,交AB于点D,交AC于点E,点F为BC边上一点,AF与DE交于点G.若 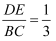 ,则
,则  .
.
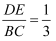 ,则
,则  .
. 
如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD= .

在△ABC中,∠C=90°,如果AB=2,BC=1,那么∠A的度数为( )
A . 30°
B . 45°
C . 60°
D . 90°
最近更新
- 阅读理解 Mrs. Jackson is anAmerican doctor. She is now in China.
- 下列实验操作中错误的是 A. 过
- 已知点A、B、C的坐标分别是(2,-4)、(0,6)、(-8,10),则+2=___________,- =______
- 看2015年3月13日天气预报图,回答问题。(1)描述沙尘暴分布范围,分析沙尘暴的成因。(6分) (2)结
- 阅读下面的《孟子》选段,回答问题。 (一)曰:“敢问国君欲养君子,如何斯可谓养矣?” 曰:“以君命将之,再拜稽首而受。其
- 如图7所示,在光滑水平面上有坐标系xOy,质量为1 kg的质点开始静止在xOy平面上的原点O处,某一时刻起受到沿x轴正方
- 一个物体从静止开始做匀加速直线运动。它在第一秒内与在第二秒内位移之比为S1 : S2 ,在走完第1m时与走完第2m时的速
- Last month, our English Department invited a local radio sta
- 2010年12月发生的义煤集团兼并重组的巨源煤矿瓦斯爆炸事故,共造成26人遇难。遏制重特大安全事故的发生,是我国目前安全
- I advise you to take school more seriously, otherwise you' 1
- 《法兰西第三共和国宪法》规定:“总统有权召开两院的特别会议。在会议的闭会时期,如果两院有绝对多数要求开会,总统也必须召集
- 党的十八大以来,反腐败斗争不断深入,惩治腐败一直保持高压态势。先后有多位副国级和省部级高官被查处。腐败高官被依法查处 ①
- 文学艺术对于反映人们的精神生活、展示人们的精神世界有独特的作用。中华文化中的文学艺术展现了中华民族的精神向往和美好追求,
- 2010年1月22日,江苏省宣布自2月1日起提高最低工资标准。其后,许多省份陆续提高了最低工资标准。这表明了政府(
- 若|a|=,|b|=2,且(a-b)⊥a,则a与b的夹角是A. B.
- 某学习小组利用银边天竺葵(叶片边缘部分呈白色)探究阳光与有机物的关系,实验过程如图所示(其中把B处两面用黑纸片遮盖上),
- 人类每时每刻都离不开空气,没有空气就没有生命,也就没有生机勃勃的地球。 (1)空气主要由 (填物质名称
- 下列各句中,加点的成语使用不正确的一项是 A.只要你能力我身临其境的想一想,你就不会对我求全责备了。 B.是深入了解
- (12分)质量为25kg的小孩坐在秋千上,小孩离栓绳子的横梁2.5 m.如果秋千摆到最高点时,绳子与竖直方向的夹角是6
- 38.4g铜跟适量的浓HNO3反应,铜全部作用后,共收集到气体22.4L(标准状况下),反应消耗的HNO3的物质的量可能



