九年级(初三)数学下学期下册试题
在矩形ABCD中,BC=6,点E是AD边上一点,∠ABE=30°,BE=DE,连接BD.动点M从点E出发沿射线ED运动,过点M作MN∥BD交直线BE于点N.

-
(1) 如图1,当点M在线段ED上时,求证:MN=
 EM;
EM;
-
(2) 设MN长为x,以M、N、D为顶点的三角形面积为y,求y关于x的函数关系式;
-
(3) 当点M运动到线段ED的中点时,连接NC,过点M作MF⊥NC于F,MF交对角线BD于点G(如图2),求线段MG的长.
图、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,线段AB的端点均在格点上.在图②、图③中仿照图①,只用无刻度的直尺,各画出一条线段CD,将线段AB分为23两部分。
要求:所画线段CD的位置不同,点C、D均在格点上。

如图,M为反比例函数y= 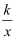 图象上一点,MA⊥y轴于点A,S△MAO=2时,k=.
图象上一点,MA⊥y轴于点A,S△MAO=2时,k=.
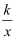 图象上一点,MA⊥y轴于点A,S△MAO=2时,k=.
图象上一点,MA⊥y轴于点A,S△MAO=2时,k=. 
如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为.

有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6,甲、乙、丙三位同学从三个不同的角度去观察此正方体,观察结果如图所示:

请画出正方体的一种表面展开图,(要求把数字标注在表面展开图中)
如图,在 中,
中, , 若
, 若 , 则
, 则 ( )
( )
 中,
中, , 若
, 若 , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,  中,
中,  ,
,  ,
, 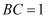 ,以点B为圆心,以BC长度为半径作弧,交BA于点D , 以点C为圆心,以大于
,以点B为圆心,以BC长度为半径作弧,交BA于点D , 以点C为圆心,以大于  为半径作弧,接着再以点D为圆心,以相同长度为半径作弧,两弧交于点E , 作射线BE交CA于点F , 以点B为圆心,以BF为长度作弧,交BA于点G , 则阴影部分的面积为.
为半径作弧,接着再以点D为圆心,以相同长度为半径作弧,两弧交于点E , 作射线BE交CA于点F , 以点B为圆心,以BF为长度作弧,交BA于点G , 则阴影部分的面积为.
 中,
中,  ,
,  ,
, 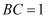 ,以点B为圆心,以BC长度为半径作弧,交BA于点D , 以点C为圆心,以大于
,以点B为圆心,以BC长度为半径作弧,交BA于点D , 以点C为圆心,以大于  为半径作弧,接着再以点D为圆心,以相同长度为半径作弧,两弧交于点E , 作射线BE交CA于点F , 以点B为圆心,以BF为长度作弧,交BA于点G , 则阴影部分的面积为.
为半径作弧,接着再以点D为圆心,以相同长度为半径作弧,两弧交于点E , 作射线BE交CA于点F , 以点B为圆心,以BF为长度作弧,交BA于点G , 则阴影部分的面积为. 
试举例说明反比例函数y= 等所能表示的实际意义.
等所能表示的实际意义.
 等所能表示的实际意义.
等所能表示的实际意义.
小强和小明同学在学习了“平面镜反射原理后,”自己用一个小平面镜MN做实验.他们先将平面镜放在平面上,如图,用一束与平面成30°角的光线照射平面镜上的A处,使光影正好落在对面墙面上一幅画的底边C点,他们不改变光线的角度,原地将平面镜转动了7.5°角,即∠MAM′=7.5°,使光影落在C点正上方的D点,测得CD=10cm,求平面镜放置点与墙面的距离AB.(  ≈1.73,结果精确到0.1).
≈1.73,结果精确到0.1).
 ≈1.73,结果精确到0.1).
≈1.73,结果精确到0.1). 
下列哪个图形,主视图、左视图和俯视图相同的是( )




A . 圆锥
B . 圆柱
C . 三棱柱
D . 正方体
下列各图中,经过折叠能围成一个立方体的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
画出下边图形从正面、左面、上面看到的几何体的形状.

函数y=  的图象大致是( )
的图象大致是( )
 的图象大致是( )
的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=  (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.

-
(1) 若EB=
 OD,求点E的坐标;
OD,求点E的坐标;
-
(2) 若四边形ABCD为平行四边形,求过A、D两点的函数关系式.
在直角三角形中各边都扩大2倍,则锐角A的正弦值与余弦值都( )
A . 缩小2倍
B . 扩大2倍
C . 不变
D . 不能确定
若点(3,4)是反比例函数  图象上一点,则此函数图象必经过点( )
图象上一点,则此函数图象必经过点( )
 图象上一点,则此函数图象必经过点( )
图象上一点,则此函数图象必经过点( )
A . (2,6)
B . (2,-6)
C . (4,-3)
D . (3,-4)
如图,直线  与
与  轴、
轴、  轴分别交于
轴分别交于  两点,与双曲线
两点,与双曲线  交于
交于  两点,且
两点,且  .
.
 与
与  轴、
轴、  轴分别交于
轴分别交于  两点,与双曲线
两点,与双曲线  交于
交于  两点,且
两点,且  .
. 
-
(1) 求反比例函数解析式;
-
(2) 求
 的面积.
的面积.
如图,Rt△OAB的边AB延长线与反比例函数y=  在第一象限的图象交于点C , 连接OC , 且∠AOB=30°,点C的纵坐标为1,则△OBC的面积是.
在第一象限的图象交于点C , 连接OC , 且∠AOB=30°,点C的纵坐标为1,则△OBC的面积是.
 在第一象限的图象交于点C , 连接OC , 且∠AOB=30°,点C的纵坐标为1,则△OBC的面积是.
在第一象限的图象交于点C , 连接OC , 且∠AOB=30°,点C的纵坐标为1,则△OBC的面积是. 
在一次夏令营活动中,小霞同学从营地A地出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C , 此时小霞在B地的( )
A . 北偏东20°方向上
B . 北偏西20°方向上
C . 北偏西30°方向上
D . 北偏西40°方向上
感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)

-
(1) 探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
-
(2) 拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6
 ,BD=4,则DE的长为.
,BD=4,则DE的长为.
最近更新
- 铁钉刺入某人的脚底,随即她产生了一系列的反应。此人脚底受伤后出现了红肿,医生担心她感染破伤风杆菌,立刻给她注射疫苗进行应
- 两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A、B旋转,如果两条平行直线间的距离为d,求: (
- 下列实验操作正确的是( )A. 稀释浓硫酸 B.粗食盐水过滤 C.点燃酒精灯
- 下面加点字的注音全部正确的一组是( ) A.深邃(suí) 不列颠尼亚(diān)
- --Would you like tea or coffee? -- ________.I prefer water.
- 请分析下列材料:我国2007年6月29日通过的《劳动合同法》规定,劳动者在试用期的工资不得低于用人单位所在地的最低工资标
- 下列有关生物技术引起的伦理问题的叙述,不正确的是 () A.人们现在的伦理道德观念还不能接受克隆人 B.设计试管婴儿是为
- 用水平力F推静止在斜面上的物块,当力F由零开始逐渐增大而物块仍保持静止状态,则物块:( )A、所受合力逐渐增大;
- (2011•杭州)日本福岛核电站发生事故以来,目前在我国各地监测出的人工放射物质碘﹣131(碘元素符号:I)的数值水平极
- 绿色荧光蛋白简称GFP,最初是从维多利亚多管发光水母中分离出来的结构蛋白。其相关数据如下图所示,下列有关叙述正确的是A.
- 西塞罗说:“执政官乃是会说话的法律,而法律乃是不会说话的执政官。”对于这句话的解释,最正确的是 A.法律面前人人平等
- 已知定义域为R的奇函数f(x)的导函数为f'(x),当x>0时,f'(x)+>0,若a=f,b=-2f(-2
- 如图所示电路中,电源电压不变,闭合开关S,当滑动变阻器的滑片P向左移动时: A.电流表示数变大,电压表示数变大 B.电流
- 下列有关物质用途的描述中,错误的是( ) A.氢气作清洁燃料 B. 氮气用作焊接金属的保护气
- 在一定条件下,下列物质的转化一步不可能实现的是 A.Fe→Fe3O4
- 关于近代物理学的结论中,哪些是正确的: ( ) A.宏观物体的物质波波长非常小,极易
- 已知在中,,,求其他边和角.
- (2011•德州)在直角坐标系xoy中,已知点P是反比例函数(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切
- (14分)A为药用有机物,A存在如下图所示的转化关系。已知A在一定条件下能跟醇发生酯化反应,A分子中苯环上的两个取代基处
- 阅读下面的文言文,完成下列小题。 养 才 苏 洵 奇杰之士,常好自负,疏隽傲诞,不事绳检,往往冒法律,触刑禁,叫号欢呼,



