九年级(初三)数学下学期下册试题
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A . OM的长
B . 20M的长
C . CD的长
D . 2CD的长
如图,在△ABC中,D、E分别是AB、AC的中点,若△ADE的面积是a,则四边形BDEC的面积是( )

A . a
B . 2a
C . 3a
D . 4a
下列计算错误的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )

A . 俯角67°方向
B . 俯角23°方向
C . 仰角67°方向
D . 仰角23°方向
如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
这些函数(x是自变量)中,是反比例函数的是( )
A . 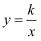 B . 5x+4y=0
C . xy﹣
B . 5x+4y=0
C . xy﹣ =0
D . y=
=0
D . y=
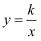 B . 5x+4y=0
C . xy﹣
B . 5x+4y=0
C . xy﹣ =0
D . y=
=0
D . y=
如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )

A . sinA的值越小,梯子越陡
B . cosA的值越小,梯子越陡
C . tanA的值越小,梯子越陡
D . 陡缓程度与∠A的函数值无关
如图,P1、P2、P3是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形P1A10,P2A20,P3A30,设它们的面积分别是S1、S2、S3 , 则( )
A . S1<S2<S3
B . S2<S1<S3
C . S1<S3<S2
D . S1=S2=S3
将图1围成图2的正方体,则图1中的红心“ ”标志所在的正方形是正方体中的( )
”标志所在的正方形是正方体中的( )

A . 面CDHE
B . 面BCEF
C . 面ABFG
D . 面ADHG
下列函数中,是反比例函数的为( )
A . y=2x+1
B . y= C . y=
C . y= D . 2y=x
D . 2y=x
 C . y=
C . y= D . 2y=x
D . 2y=x
已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积之比为( )
A . 4:3
B . 3:4
C . 16:9
D . 9:16
如图所示几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,过点M(﹣3,2)分别作x轴、y轴的垂线与反比例函数y=  的图象交于A,B两点,则四边形MAOB的面积为.
的图象交于A,B两点,则四边形MAOB的面积为.
 的图象交于A,B两点,则四边形MAOB的面积为.
的图象交于A,B两点,则四边形MAOB的面积为.
下列各图中有可能是函数y=ax2+c,  的图象是( )
的图象是( )
 的图象是( )
的图象是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在  中,DE∥BC,
中,DE∥BC,  ,
,  ,
,  ,则
,则  的长为( )
的长为( )
 中,DE∥BC,
中,DE∥BC,  ,
,  ,
,  ,则
,则  的长为( )
的长为( )

A . 6
B . 7
C . 8
D . 9
如图,AB是⊙O的直径,AC是⊙O的一条弦,点P是⊙O上一点,且PA=PC,PD∥AC,与BA的延长线交于点D.

-
(1) 求证:PD是⊙O的切线.
-
(2) 若tan∠PBA=
 ,AC=12,求直径AB的长.
,AC=12,求直径AB的长.
一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为.
如图,在△ABC中,矩形DEFG,G、F在BC上,D、E分别在AB、AC上,AH⊥BC交DE于M,DG∶DE=1∶2,BC=12 cm,AM=8 cm,求矩形的各边长.

如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )

A . BC= B . CD=AD•tanα
C . BD=ABcosα
D . AC=ADcosα
B . CD=AD•tanα
C . BD=ABcosα
D . AC=ADcosα
 B . CD=AD•tanα
C . BD=ABcosα
D . AC=ADcosα
B . CD=AD•tanα
C . BD=ABcosα
D . AC=ADcosα
某几何体由一些大小相同的小正方体组成,如图是它的俯视图和主视图,那么组成该几何体的小正方体的个数最少为( )

A . 4个
B . 5个
C . 6个
D . 7个
最近更新
- 有学者认为,中国古代中枢权力机构变迁的一条主线是内廷机构的不断放大、外迁。下列变化过程能够说明这一观点的是 A.从分封制
- 20世纪中期,美国财政部长福勒之所以得意地宣称“各个行星围绕着太阳转,各国货币围绕着美元转”是源于 A.《关税与
- 下列函数中不是幂函数的是( )A.y= B.y=x3
- 如图所示,四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是BD,AC的中点。 (1) 求证:AE=CE(2)
- 一只氖管的起辉电压与交变电流u=50sin314t(V)的有效值相等,若将此交变电流接到氖管的两极,在一个周期内,氖管的
- 已知Cu2S与某浓度的硝酸反应时,生成硝酸铜和硫酸,若反应中Cu2S与HNO3 的物质的量之比为2:13,则该反应的还哎
- 下列对辩证否定的理解,错误的是 A.辩证的否定是“扬弃”B.辩证的否定是既克服又保留 C.辩证的否定是事物联系和发展的环
- 27.将萤火虫腹部末端的发光器切下,干燥后研成粉末。将粉末装入试管,滴加蒸馏水,使之混合,则有淡黄色荧光出现,2min后
- 下列各组离子能在指定溶液中大量共存的一组是() A.在稀盐酸中:Ba2+、CO32﹣、Zn2+ B.在氢氧化钠溶液中:H
- 管理学上有一条定律叫“金鱼缸效应”,指的是金鱼缸是透明的,不论从哪个角度观察,里面的情况都一清二楚。这启示我们,广大党
- —What would you like _____ on Sundays? —I feel like ____ sho
- 已知GPS卫星的轨道距地面的高度约为地球半径的2倍,则GPS卫星与近地卫星的运行周期之比约为: A. B.
- 汶川地震发生后,中央和地方财政调拨专项资金,安置灾民,帮助灾民重建家园。这表明 A.财政是巩固国家政权的物质保障
- 下图为四个国家的人口出生率和死亡率图,读图完成1~4题。1.③国人口自然增长率约为 A.1% B.
- 如果2(x+3)的值与3(1-x)的值互为相反数,求x的值.
- 下列物质的转化在给定条件下能实现的是 ( )
- 我国已初步建立起全面的行政监督体系,下列属于政府系统内部的监督有 A.人民代表大会的监督
- 现有铁、稀盐酸、氢氧化钠溶液、氧化铁、硫酸铜溶液五种物质,它们之间相互反应情况如下图,“—”连接的两种物质能反应。请回答
- 微信营销是伴随着微信的火热而兴起的一种网络营销方式,越来越多的商家以及个人选择在微信端进行营销。材料表明 ①新兴媒体已成
- We made much money we bought a new house before lo



