九年级(初三)数学下学期下册试题
如图,点  ,
,  在反比例函数
在反比例函数  的图象上,点
的图象上,点  在反比例函数
在反比例函数  的图象上,连接
的图象上,连接  ,
,  ,且
,且  轴,
轴,  轴,
轴, 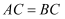 .若点
.若点  的横坐标为2,则
的横坐标为2,则  的值为.
的值为.
 ,
,  在反比例函数
在反比例函数  的图象上,点
的图象上,点  在反比例函数
在反比例函数  的图象上,连接
的图象上,连接  ,
,  ,且
,且  轴,
轴,  轴,
轴, 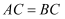 .若点
.若点  的横坐标为2,则
的横坐标为2,则  的值为.
的值为. 
如图,点A在反比例函数y= 的图象上,过点A作AB⊥x轴于点B,C为x轴正半轴上一点,连接AC交y轴于点D, tan∠ACB=
的图象上,过点A作AB⊥x轴于点B,C为x轴正半轴上一点,连接AC交y轴于点D, tan∠ACB= , AO平分∠CAB,
, AO平分∠CAB, , 则k=
, 则k=
 的图象上,过点A作AB⊥x轴于点B,C为x轴正半轴上一点,连接AC交y轴于点D, tan∠ACB=
的图象上,过点A作AB⊥x轴于点B,C为x轴正半轴上一点,连接AC交y轴于点D, tan∠ACB= , AO平分∠CAB,
, AO平分∠CAB, , 则k=
, 则k= 
在  中,
中,  ,点
,点  在
在  边上,
边上,  ,分别连接
,分别连接  .
.
 中,
中,  ,点
,点  在
在  边上,
边上,  ,分别连接
,分别连接  .
.

-
(1) 如图1,
 三点在同一条直线上.
三点在同一条直线上.
①若
 ,求
,求  的长;
的长;②求证:
 .
. -
(2) 如图2,若
 ,
,  分别是
分别是  的中点,求
的中点,求  的值.
的值.
码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.
-
(1) 轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
-
(2) 由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
-
(3) 若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?
如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°..则AD2= ,依此类推这样做的第n个菱形ABnCnDn的边ADn
的长是 .

如图,为了测量水塘边A、B两点之间的距离,在可以看到的A、B的点E处,取AE、BE延长线上的C、D两点,使得CD∥AB,若测得CD=5m,AD=15m,ED=3m,则A、B两点间的距离为m.

如果y与y1成正比例,y1与x成反比例,且y关于x的函数图象经过点(  ,﹣1),那么y关于x的函数解析式是.
,﹣1),那么y关于x的函数解析式是.
 ,﹣1),那么y关于x的函数解析式是.
,﹣1),那么y关于x的函数解析式是.
如图,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,  .E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,
.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,  .
.
 .E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,
.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,  .
. 
-
(1) 求AB的长;
-
(2) 当点G在线段AD上时,求y关于x的函数解析式,并写出函数的定义域;
-
(3) 如果
 ,求线段CE的长.
,求线段CE的长.
河堤横截面如图所示,堤高  为4米,迎水坡
为4米,迎水坡  的坡比为1:
的坡比为1:  (坡比=
(坡比=  ),那么
),那么  的长度为米.
的长度为米.
 为4米,迎水坡
为4米,迎水坡  的坡比为1:
的坡比为1:  (坡比=
(坡比=  ),那么
),那么  的长度为米.
的长度为米. 
某村粮食总产量为a(a为常量)吨,设该村粮食的人均产量y(吨),人口数为x(人),则y与x之间的函数图象应为图中的( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知点A(2,3)在反比例函数  的图象上,则k的值是( )
的图象上,则k的值是( )
 的图象上,则k的值是( )
的图象上,则k的值是( )
A . ﹣7
B . 7
C . ﹣5
D . 5
如图为三个并列的边长相同的正方形,试说明:∠1+∠2+∠3=90°.

下列关系式中,y为x的反比例函数的是( )
A . xy=13
B .  =3
C . y=﹣x
D . y=x+1
=3
C . y=﹣x
D . y=x+1
 =3
C . y=﹣x
D . y=x+1
=3
C . y=﹣x
D . y=x+1
如图所示的几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B . 如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.

-
(1) ①填空:△ACE∽∽;
-
(2) 求证:△CDE∽△CBA;
-
(3) 求证:△FBD≌△EDC;
-
(4) 若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由.
如图所示是由棱为1cm的立方体小木块搭建成的几何体从3个方向看到的形状图.

-
(1) 请你观察它是由 个立方体小木块组成的;
-
(2) 在从上面看到的形状图中标出相应位置上立方体小木块的个数;
-
(3) 求出该几何体的表面积(包含底面).
已知△ABC和△A′B′C′是位似图形.△A′B′C′的面积6cm2 , 周长是△ABC的一半.AB=8cm,则AB边上的高等于( )
A . 3cm
B . 6cm
C . 9cm
D . 12cm
如图,在  中,
中,  是
是  边中线.延长
边中线.延长 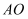 至点B,作
至点B,作  的角平分线
的角平分线  ,过点C作
,过点C作  于点F.
于点F.
 中,
中,  是
是  边中线.延长
边中线.延长 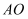 至点B,作
至点B,作  的角平分线
的角平分线  ,过点C作
,过点C作  于点F.
于点F. 
-
(1) 求证:四边形
 是矩形;
是矩形;
-
(2) 连接
 ,若
,若  ,求
,求  的长.
的长.
如图,是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图折成正方体后,相对面上的两个数互为相反数,则填在B内的数为.

若反比例函数  的图象在第二,四象限,则m的值是( )
的图象在第二,四象限,则m的值是( )
 的图象在第二,四象限,则m的值是( )
的图象在第二,四象限,则m的值是( )
A . −1或1
B . 小于12的任意实数
C . −1
D . 不能确定
最近更新
- 如图所示,均匀的长方形薄片合金电阻板abcd,ab连长为L1,ad连长为L2,当端点Ⅰ、Ⅱ或Ⅲ、Ⅳ接入电路时,RⅠⅡ:R
- 25℃和101kPa时,乙烷、乙炔和丙烯组成的混合烃32mL,与过量氧气混合并完全燃烧,除去水蒸气,恢复到原来的温度和压
- (1)物质的分类标准有多种,标准可以是物质的组成、性质、用途等。请根据所学知识,依据物质所具有的某种性质,自拟分类标准,
- “分封制是一柄双刃剑,它同时给予中央集权和地方势力以合法性。至于哪种势力能够在激烈的政治搏斗中取胜,那就完全要看他的实力
- 下列单位中与磁感应强度的单位“特斯拉”相当的是() A.Wb/m 2 B.N/A·mC
- 在一块草原上有8户牧民,每户牧民各养了一群羊,其中有6户养的是绵羊,有2户养的是山羊,这块草原上的8群羊是() A.6个
- Don’t eat too much chocolate, or you can ______ weight quic
- 根据短文内容,用适当的单词的适当形式填空。(C)RouteFlight No.DayDeparture(离开) Time
- 补写出下列各篇名句中的空缺部分。 (1)飞来山上千寻塔,闻说鸡鸣见日升。,。 (王安石《登飞来峰》) (2)予观夫巴陵胜
- 在测量电阻的实验中,选用4节干电池作电源,待测电阻约15欧,则在实验中电流表和电压表的量程分别选用_____安和____
- What is “Walk to School”? Now we are working on a programmed
- 《旧唐书》记载:长庆元年(821年),唐穆宗要破格提拔前代理大理少卿刘士泾为太仆卿,给事中(门下省属官)韦弘最、薛存庆封
- 下列4个命题:①四面体的四个面至多只能有三个直角三角形;②一条直线与一个直二面角的两个面所成角分别为α、β,则α+β>9
- 计算: .
- 《西南政法大学学报》刊载的《女生就业的比较与分析》一文,有一组对某大学法学专业男女本科毕业生就业情况调查表。请根据调查表
- 2010年9月20日人民网载文指出,山西省阳泉市郊区检察院日前批准逮捕该公司法定代表人兼总经理王志刚等7名涉案生产销售有
- 漫画《教育流水线》违背的哲学原理是A.矛盾存在于一切事物之中B.学生要肩负起神圣的时代使命C.哲学是人认识世界的科学工具
- 生活在高原上的人们,血液中的红细胞数量较多,出现此生理现象的主要原因是下列哪种生态因素造成的 ( )
- 一个氘核()与一个氚核()发生聚变,产生一个中子和一个新核,并出现质量亏损。聚变过程中 A.吸收能量,生成的新核是
- I’m puzzled by this question. Youmay ask ________ knows be



