九年级(初三)数学下学期下册试题
小明沿着坡度i为1∶  的直路向上走了50 m,则小明沿垂直方向升高了m.
的直路向上走了50 m,则小明沿垂直方向升高了m.
 的直路向上走了50 m,则小明沿垂直方向升高了m.
的直路向上走了50 m,则小明沿垂直方向升高了m.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,DE=2,BC=3,求  的值.
的值.
 的值.
的值. 
白天,小明和小亮在阳光下散步,小亮对小明说:“咱俩的身高都是已知的.如果量出此时我的影长,那么我就能求出你此时的影长.”晚上,他们二人有在路灯下散步,小明想起白天的事,就对小亮说“如果量出此时我的影长,那么我就能求出你此时的影长”.你认为小明、小亮的说法有道理吗?说说你的理由.
如图,在△ABC中,D,E分别是边AB,AC的中点,则△ADE与四边形BCED的面积比S△ADE:S四边形BCED=.

将一个正方体的表面沿某些棱剪开,其展开图如图,则该正方体中与“我”字相对的字是.

如图,在平面直角坐标系中,  与
与  位似,位似中心是原点
位似,位似中心是原点  ,若
,若  与
与  的相似比为
的相似比为  ,已知
,已知  ,则它对应点
,则它对应点 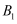 的坐标是( )
的坐标是( )
 与
与  位似,位似中心是原点
位似,位似中心是原点  ,若
,若  与
与  的相似比为
的相似比为  ,已知
,已知  ,则它对应点
,则它对应点 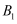 的坐标是( )
的坐标是( )

A .  B .
B . 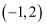 C . (-9,1) 或 (9,-1)
D .
C . (-9,1) 或 (9,-1)
D .  或
或 
 B .
B . 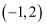 C . (-9,1) 或 (9,-1)
D .
C . (-9,1) 或 (9,-1)
D .  或
或 
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=10m,塔影长DE=20m,小惠和小岚的身高都是1.60m,同一时刻,小惠站在点E处,影子在坡面上,小岚站在平地上,影子也在平地上,两人的影长分别是2m和1m,试求塔高AB.

由几个相同的边长为1的小立方块搭成的几何体从上面看到的视图如图,方格中的数字表示该位置的小立方块的个数  请在下面方格纸中分别画出这个几何体从正面看和从左面看到的视图.
请在下面方格纸中分别画出这个几何体从正面看和从左面看到的视图.
 请在下面方格纸中分别画出这个几何体从正面看和从左面看到的视图.
请在下面方格纸中分别画出这个几何体从正面看和从左面看到的视图. 

在反比例函数  的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
 的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
A . k>1
B . k>0
C . k≥1
D . k<1
当锐角 时,
时, 的值是( )
的值是( )
 时,
时, 的值是( )
的值是( )
A . 大于 B . 小于
B . 小于 C . 大于
C . 大于 D . 小于
D . 小于
 B . 小于
B . 小于 C . 大于
C . 大于 D . 小于
D . 小于
一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后,到达B处,在B处测得灯塔C北偏西60°方向上,当轮船到达灯塔C的正东方向的D处时,如图所示,求轮船与灯塔C的距离(结果保留根号)?

如图,在△ABC中,AD是BC边上的高,AB=5,AD=4,BC=3+4  。
。
 。
。 
-
(1) BD的长为,sin∠ABC=.
-
(2) 求∠DAC的度数.
小红沿坡比为1:  的斜坡上走了100米,则她实际上升了米.
的斜坡上走了100米,则她实际上升了米.
 的斜坡上走了100米,则她实际上升了米.
的斜坡上走了100米,则她实际上升了米. 
如图,操场上有一根旗杆AH.为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?

计算:  .
.
 .
.
已知  ,那么锐角
,那么锐角  的取值范围是( )
的取值范围是( )
 ,那么锐角
,那么锐角  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
-
(1) 求v关于t的函数表达式;
-
(2) 方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
某高铁路段修建过程中需要经过一座小山.如图,施工方计划沿  方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得
方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得  ,
,  ,
,  ,则
,则  的长为.(结果保留根号)
的长为.(结果保留根号)
 方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得
方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得  ,
,  ,
,  ,则
,则  的长为.(结果保留根号)
的长为.(结果保留根号) 
已知sin46°=cosα,则α=度.
如图所示的几何体的左视图为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 根据给出的数塔猜测123 456×9+7等于( )1×9+2=1112×9+3=111123×9+4=1 1111
- 在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续
- 据科学测算,1926—1933年间,欧洲与美洲之间的距离平均每年增加65厘米。这说明( ) A.大西洋在扩张
- 改革开放后,中国的工业化有了长足的进步,在基本建设和技术改革方面的重大成就是( ) A.积极扶植乡镇企业,开辟了工
- 如图为细胞融合的简略过程,请据图回答:(1)若A、B是植物细胞,在细胞融合之前已处理,除去了______________
- “花气袭人知骤暖,鹊声穿树喜新晴。”这是宋代诗人陆游《村居书喜》中的一句诗。诗中描述的“花气袭人”现象表明:分子在
- (08年永定一中二模理)(12分)如图,四棱锥中,底面是边长为2的正方形,,且,为中点.(1)求证:平面; (2)
- 血液与组织细胞进行物质交换的是 A. 心脏 B.动脉
- The Norwegian government is doing its best to keep the oil i
- They want to know do to help us. A.what can th
- 小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是(
- 化纤衣服很容易沾上灰尘,这是因为它( ) A. 容易积累静电荷 B. 具有一
- 下列各组离子在指定溶液中一定能大量共存的是( ) A.滴入酚酞显红色的溶液中:NH4+、Mg2+、F—、NO3-
- 将32.64 g铜与140mL一定浓度的硝酸反应,铜完全溶解产生的NO和NO2混合气体在标准状况下的体积为11.2 L。
- 下表为广州市人口迁移统计表,根据所学人口迁移知识,认真分析该表回答下列问题。 广州市人口迁移统计表项目 年份 迁入(
- “人间四月芳菲尽,山寺桃花始盛开”造成这一差异的主要环境因素是 ( ) A、阳光 B、温度
- (06年重庆卷)是一种半衰期为5730年的放射性同位素。若考古工作者探测某古木中的含量为原来的,则该古树死亡时间距今大约
- 29.家兔的神经系统是由___________、___________和___________组成。家兔的许多活动比较复
- 某汽车以恒定功率P、初速度v0冲上倾角一定的斜坡时,汽车受到的阻力恒定不变,则汽车上坡过程的v-t图象不可能 是下图中的
- 如图反映的是新中国在20世纪五六十年代的农业经济发展状况,出现图中B点到C点这一变化的主要原因是( )A. 经济建设没



