九年级(初三)数学下学期下册试题
如图,在△ABC中,∠BAC=90°,∠C=30°,按以下步骤作图:分别以点B,C力圆心,以大于 BC的长为半径作弧,两弧交于M,N两点,作直线MN,与边AC,BC 分别交于D,E两点,连接BD,AE,若AE=6,则△BCD的周长为( )
BC的长为半径作弧,两弧交于M,N两点,作直线MN,与边AC,BC 分别交于D,E两点,连接BD,AE,若AE=6,则△BCD的周长为( )
 BC的长为半径作弧,两弧交于M,N两点,作直线MN,与边AC,BC 分别交于D,E两点,连接BD,AE,若AE=6,则△BCD的周长为( )
BC的长为半径作弧,两弧交于M,N两点,作直线MN,与边AC,BC 分别交于D,E两点,连接BD,AE,若AE=6,则△BCD的周长为( )

A . 6+3 B . 6+4
B . 6+4 C . 12+8
C . 12+8 D . 12+4
D . 12+4
 B . 6+4
B . 6+4 C . 12+8
C . 12+8 D . 12+4
D . 12+4
计算: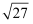 -3sin60°-cos30°+2tan45°.
-3sin60°-cos30°+2tan45°.
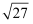 -3sin60°-cos30°+2tan45°.
-3sin60°-cos30°+2tan45°.右图可以折叠成的几何体是()
A . 三棱柱
B . 四棱柱
C . 圆柱
D . 圆锥
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )

A .  B .
B .  C .
C .  D .
D . 
在同一平面内,如果仅原点重合的两条数轴不垂直,我们将这样的坐标系称为斜坐标系.如图1,若点P是斜坐标系  中任意一点,过点Р分别作两坐标轴的平行线,与x轴,y轴交于点M,N,如果点M,N对应的实数为a,b,则点P的坐标为
中任意一点,过点Р分别作两坐标轴的平行线,与x轴,y轴交于点M,N,如果点M,N对应的实数为a,b,则点P的坐标为 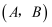 .
.
 中任意一点,过点Р分别作两坐标轴的平行线,与x轴,y轴交于点M,N,如果点M,N对应的实数为a,b,则点P的坐标为
中任意一点,过点Р分别作两坐标轴的平行线,与x轴,y轴交于点M,N,如果点M,N对应的实数为a,b,则点P的坐标为 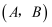 .
.

-
(1) 如图1,点E在斜坐标系
 中的坐标为( )
A .
中的坐标为( )
A . B .
B . 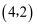 C .
C . 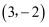 D .
D . 
-
(2) 如图2,在斜坐标系
 中,直线l与x轴,y轴交于点
中,直线l与x轴,y轴交于点  ,
,  .
.
①若点
 是直线l上一点,请写出y关于x的关系式,并就点Q在BA延长线上时的情况进行证明;
是直线l上一点,请写出y关于x的关系式,并就点Q在BA延长线上时的情况进行证明;②若x轴与y轴的夹角
 ,经过原点О的直线m交直线l于点F,当
,经过原点О的直线m交直线l于点F,当  时,请直接写出点F的坐标.
时,请直接写出点F的坐标.
如图,  内接于
内接于  ,
,  ,
,  ,
,  于点
于点  ,若
,若  的半径为
的半径为  ,则
,则  的长为.
的长为.
 内接于
内接于  ,
,  ,
,  ,
,  于点
于点  ,若
,若  的半径为
的半径为  ,则
,则  的长为.
的长为. 
如图,在 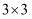 的网格中,A,B均为格点,以点A为圆心,以AB的长为半径作弧,图中的点C是该弧与格线的交点,则
的网格中,A,B均为格点,以点A为圆心,以AB的长为半径作弧,图中的点C是该弧与格线的交点,则  的值是( )
的值是( )
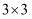 的网格中,A,B均为格点,以点A为圆心,以AB的长为半径作弧,图中的点C是该弧与格线的交点,则
的网格中,A,B均为格点,以点A为圆心,以AB的长为半径作弧,图中的点C是该弧与格线的交点,则  的值是( )
的值是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在Rt△ABC中,∠C=90°,AB=10,cos∠B=  ,则BC=( )
,则BC=( )
 ,则BC=( )
,则BC=( ) 
A . 6
B . 8
C . 9
D . 15
一个几何体的三视图如图所示,则这个几何体是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在  中,
中, 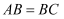 ,
,  .按以下步骤作图:①分别以点A,B为圆心,以大于
.按以下步骤作图:①分别以点A,B为圆心,以大于  长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则
长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则  .
.
 中,
中, 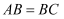 ,
,  .按以下步骤作图:①分别以点A,B为圆心,以大于
.按以下步骤作图:①分别以点A,B为圆心,以大于  长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则
长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则  .
.

如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为 m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)

抛物线 
 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( )

 在同一平面直角坐标系内的图象大致为( )
在同一平面直角坐标系内的图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知扇形OAB的半径为6cm,圆心角的度数为120°,若将OA,OB重合后围成一圆锥侧面,那么圆锥的底面半径为( )

A . 2cm
B . 3cm
C . 6cm
D . 2 cm
cm
 cm
cm
某同学设计了如下杠杆平衡实验:如图,取一根长65cm的质地,均匀木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧,距离中点20cm处挂一个重9N的物体,在中点的右侧,用一个弹簧测力计向下拉,使木杆保持平衡(动力×动力臂=阻力×阻力臂),改变弹簧测力计与中点O的距离L(单位:cm),观察弹簧测力计的示数F(单位:N). 通过实验,得到下表数据:
|
第1组 |
第2组 |
第3组 |
第4组 |
第5组 |
|
|
L/cm |
20 |
24 |
25 |
28 |
30 |
|
F/N |
9 |
7.5 |
10 |
6 |
-
(1) 你认为表中哪组数据是明显错误的.
-
(2) 在已学过的函数中选择合适的模型,求F关于L的函数表达式.
-
(3) 若弹簧测力计的量程是10N,求L的取值范围.
如图,明明家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到这条公路的距离是( )

A .  米
B . 250米
C .
米
B . 250米
C .  米
D .
米
D .  米
米
 米
B . 250米
C .
米
B . 250米
C .  米
D .
米
D .  米
米
如图,△ABC中,∠C=90°,∠A的正切是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示的几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C . 
如图,小明站在河岸上的点G处看见河里有一只小船C沿垂直于岸边的方向划过来,此时,测得小船C的俯角是  ,若小明的眼睛与地面的距离是
,若小明的眼睛与地面的距离是  ,
,  ,
,  平行于
平行于  ,迎水坡的坡度
,迎水坡的坡度  ,坡长
,坡长  ,求小船C到岸边的距离
,求小船C到岸边的距离  的长.(参考数据:
的长.(参考数据:  ,结果保留一位小数)
,结果保留一位小数)
 ,若小明的眼睛与地面的距离是
,若小明的眼睛与地面的距离是  ,
,  ,
,  平行于
平行于  ,迎水坡的坡度
,迎水坡的坡度  ,坡长
,坡长  ,求小船C到岸边的距离
,求小船C到岸边的距离  的长.(参考数据:
的长.(参考数据:  ,结果保留一位小数)
,结果保留一位小数)

下图是由6个完全相同的小正方体搭成的几何体,它的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为2米,斜坡AB的坡度  ,现把图中的货物沿斜坡继续往前平移,当货物顶点D与C重合时,恰好可把货物放平装进货厢,则BD=.
,现把图中的货物沿斜坡继续往前平移,当货物顶点D与C重合时,恰好可把货物放平装进货厢,则BD=.
 ,现把图中的货物沿斜坡继续往前平移,当货物顶点D与C重合时,恰好可把货物放平装进货厢,则BD=.
,现把图中的货物沿斜坡继续往前平移,当货物顶点D与C重合时,恰好可把货物放平装进货厢,则BD=.

最近更新
- “零排放”是指在生产新物质的过程中,原料中的原子全部转化到欲制取的产物中,在生产过程和末端均为“零排放”,从而达到“零污
- The man managed to make himself __________ with his ________
- 以NA表示阿伏加德罗常数,下列说法正确的是 A.0.1mol Fe与足量盐酸反应,转移的电子数为0.3NA
- 运用元素周期律分析推断,下列说法不正确的是( )A.铍(Be)的氧化物的水化物可能有两性B.砹(At)为有色固体
- 如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点, 把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设
- 某元素的原子最外层电子数是次外层电子数的两倍,该元素是 ,它和氢元素组成的最简单的化合物的化学式为
- 沙漠中的仙人掌,扁平宽大的块茎可贮藏水分,刺状叶可减少水分的蒸腾散失,这说明了() A.生物适应环境
- 读“某地区城市分布图”和“甲城市地租等值线示意图”(左图)以及“甲城市某区域日均地铁分时段客运量统计图”(右图),读图完
- 有学者形容某历史事件为“两位国王主演的一出曲折的巴洛克式即兴剧,一首贵族合谱的复调音乐,几幕……军队、……市民作大合唱,
- 有下列三个结论: ①命题“”的否定是“”; ②“”是“直线与直线互相垂直”的充要条件; ③若随机变量服从正态分布,且,则
- 一打点计时器固定在倾角为θ的斜面上,一小车拖着穿过打点计时器的纸带从斜面上滑下,打出的纸带的一段如图所示.纸带上0、1、
- 2009年2月12日是伟大科学家达尔文诞生诞辰200周年,同时也是其《物种起源》出版150周年,全世界的纪念活动悄然兴起
- 2009年新中国60周年华诞,首都北京见证了新中国诞生与发展的历史依据所学知识回答下列问题。 (1)二十世纪四十年代末和
- 一个四面的所有棱长都为,四个顶点在同一球面上,则此球的表面积为 .
- 下列动物中用气囊辅助肺进行呼吸的是( )A.丹顶鹤 B.青蛙 C.扬子鳄 D
- .(10年云南玉溪15)下图是元素周期表中提供的硫元素的相关信息,对图中信息理解错误的是( )A.该元素原子的最外
- 某同学书写的试剂标签如下图所示,其中错误的是
- 已知是上的减函数,那么的取值范围是 ( ). A. B. C. D.
- 当人看到酸梅时唾液分泌会大量增加,对此现象的分析,错误的是() A. 这是一种反射活动,唾液腺的分泌物不属
- 已知双曲线=1的右焦点是F,右顶点是A,虚轴的上端点是B,·=6-4,∠BAF=150°. (1)求双曲线的方程; (2



