九年级(初三)数学下学期下册试题
关于x的一元二次方程x2﹣  x+sinα=0有两个相等的实数根,则锐角α等于( )
x+sinα=0有两个相等的实数根,则锐角α等于( )
 x+sinα=0有两个相等的实数根,则锐角α等于( )
x+sinα=0有两个相等的实数根,则锐角α等于( )
A . 15°
B . 30°
C . 45°
D . 60°
sin45°的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在△ABC中,∠ABC=90°,BC边在x轴正半轴上,中线BD的反向延长线交y轴负半轴于点E.双曲线y=  一条分支经过点A,若S△BEC=4,则k等于( )
一条分支经过点A,若S△BEC=4,则k等于( )
 一条分支经过点A,若S△BEC=4,则k等于( )
一条分支经过点A,若S△BEC=4,则k等于( ) 
A . 4
B . 8
C . 12
D . 16
如果线段a=2cm,b=18cm,那么a和b的比例中项是( )
A . 3cm
B . 4cm
C . ±6cm
D . 6cm
在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东  方向有一信号发射塔P.他由A地沿正东方向骑行
方向有一信号发射塔P.他由A地沿正东方向骑行  km到达B地,此时发现信号塔P在他的北偏东
km到达B地,此时发现信号塔P在他的北偏东  方向,然后他由B地沿北偏东
方向,然后他由B地沿北偏东  方向骑行12km到达C地.
方向骑行12km到达C地.
 方向有一信号发射塔P.他由A地沿正东方向骑行
方向有一信号发射塔P.他由A地沿正东方向骑行  km到达B地,此时发现信号塔P在他的北偏东
km到达B地,此时发现信号塔P在他的北偏东  方向,然后他由B地沿北偏东
方向,然后他由B地沿北偏东  方向骑行12km到达C地.
方向骑行12km到达C地. 
-
(1) 求A地与信号发射塔P之间的距离;
-
(2) 求C地与信号发射塔P之间的距离.(计算结果保留根号)
下列各点不在反比例函数y= 的图象上的应是( )
的图象上的应是( )
 的图象上的应是( )
的图象上的应是( )
A . (6,-2)
B . (6,2)
C . (3,4)
D . (-3,-4)
已知圆锥的底面积为16  cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .
cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .
 cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .
cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .
已知反比例函数  的图象在第二、四象限内,则a=.
的图象在第二、四象限内,则a=.
 的图象在第二、四象限内,则a=.
的图象在第二、四象限内,则a=.
如图,在等腰三角形ABC中,AB=AC,点D在BA的延长线上,BC=24, 


-
(1) 求AB的长;
-
(2) 若AD=6.5,求∠DCB的正切值
如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)

如图,已知△ABC中D为AC中点,AB=5,AC=7,∠AED=∠C,则BE=.

如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A,B两点,抛物线y=﹣x2+bx+c过A,B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.

-
(1) 求抛物线的解析式.
-
(2) 求△ABE面积的最大值.
-
(3) 连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
自“新冠”病毒出现后,瓶装酒精成了人们家中常备之物.一种酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄△BCD按压到底时,BD转动到 , 此时
, 此时 ∥EF(如图3)
∥EF(如图3)
 , 此时
, 此时 ∥EF(如图3)
∥EF(如图3)
-
(1) 求BD转动到
 扫过的面积(结果保留π);
扫过的面积(结果保留π);
-
(2) 求点D到直线EF的距离(结果精确到0.1cm).(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
已知线段  ,
,  ,
,  满足
满足  ,且
,且  .
.
 ,
,  ,
,  满足
满足  ,且
,且  .
.
-
(1) 求
 ,
,  ,
,  的值;
的值;
-
(2) 若线段
 是线段
是线段  ,
,  的比例中项,求
的比例中项,求  .
.
画出下图的三种视图.

如图,在Rt△ABC中,∠ACB=90°,sinB=  , D是BC上一点,DE⊥AB于点E,CD=DE,AC+CD=9.求BE,CE的长.
, D是BC上一点,DE⊥AB于点E,CD=DE,AC+CD=9.求BE,CE的长.
 , D是BC上一点,DE⊥AB于点E,CD=DE,AC+CD=9.求BE,CE的长.
, D是BC上一点,DE⊥AB于点E,CD=DE,AC+CD=9.求BE,CE的长.

如图,在等腰 Rt△ABC 中,∠C=90°,AC=6,D 是 AC 上一点,若 tan∠DBA=  ,则 AD 的长为( )
,则 AD 的长为( )
 ,则 AD 的长为( )
,则 AD 的长为( ) 
A . 2
B . 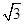 C .
C .  D . 1
D . 1
如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是( ) 

A . 正方体、圆柱、三棱柱、圆锥
B . 正方体、圆锥、三棱柱、圆柱
C . 正方体、圆柱、三棱锥、圆锥
D . 正方体、圆柱、四棱柱、圆锥
sin60°的值为( )
A .  B .
B .  C .
C . 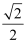 D .
D . 
 B .
B .  C .
C . 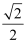 D .
D . 
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 小明翻阅家谱时看到“十一世长房:伯爵公,忠厚无华,勤力本业,家族有事,无不勉赴,不失为祖宗纯孙。”材料中的“伯爵公”最有
- 美国1787年宪法规定:国会有权宣战,招募陆军,建立和维持一支海军,有权征召民兵,以执行联邦法律、镇压叛乱和击退入侵;总
- 下图为四种不同的育种方法,请回答:(1)图中A、D途径表示杂交育种,一般从F2开始选种,这是因为 。 (2
- 2.下列各句中,没有语病的一句是( ) A.哈大高铁施行新的运行计划后,哈尔滨至北京、上海等地的部分列车也将进
- No one noticed him _____ in. A. to come B. came C. come D. h
- 下列推断正确的是 A.SiO2 是酸性氧化物,能与NaOH溶液反应 B.Na2O、Na2O2组成元素相同,与 CO2反应
- .“汉朝早期,统治者试图在周朝松散的政治联盟和秦朝严格的中央专制间走一条中间路线。”材料中的“中间路线”是指 A.郡国并
- 设x,y满足约束条件若目标函数的最大值1,则的最小值为 ( ) A.
- 日前,美国中央情报局前特工斯诺登爆光了美国的网络监视项目:“棱镜”。棱镜计划(PRISM)是一项由美国国家安全局(NSA
- 党的十七大报告指出:“初次分配和再分配都要处理好效率和公平的关系,再分配更加注重公平。”以下有利于初次分配中实现社会公平
- A、B、X、Y和Z是原子序数依次递增的短周期元素,其中A与Y同主族,X与Z同主族,A与B和X均可形成10个电子化合物;B
- 现代企业之间通过互联网建立的经常化联系,属于 A.商贸联系 B.生产协作 C.运输联系
- 实验室有:A、电磁打点计时器B、电火花计时器C.低压交流电源(周期为T),利用这些器材做“验证机械能守恒定律”实验。
- 翻译下面文言文 子见齐衰⑴者、冕衣裳者⑵与瞽者,见之,虽少,必作⑶;过之,必趋⑶。
- 直线y=2与直线的夹角是____________.
- 把直线y=-2x按向量a=(-2,1)平移后所得直线方程是( ) A.y=-2x-3
- 英国前首相丘吉尔曾经说过,我宁愿失去一个印度而不愿失去一个莎士比亚,下列文化名人中属于英国的有 ①牛顿 ②拜伦
- 解不等式-x-3>2,得其解的范围为何? (A) x<-25 (B) x>-25 (C) x<5 (D) x>5
- 若关于的一元二次方程有两个不相等的实数根,则一次函数的图象可能是
- 向正在进行有氧呼吸的细胞悬液中分别加入a、b、c、d四种抑制剂,下列正确的是 A.若d能抑制丙酮酸分解,则使葡萄糖的消耗



