九年级(初三)数学下学期下册试题
下列函数中,y是x的反比例函数的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,  为
为  的直径,
的直径,  于点
于点  ,
,  是
是  上一点,且
上一点,且  ,延长
,延长  至点
至点  ,连接
,连接 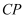 ,使
,使  ,延长
,延长  与
与  交于点
交于点  ,连结
,连结  ,
,  .
.
 为
为  的直径,
的直径,  于点
于点  ,
,  是
是  上一点,且
上一点,且  ,延长
,延长  至点
至点  ,连接
,连接 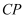 ,使
,使  ,延长
,延长  与
与  交于点
交于点  ,连结
,连结  ,
,  .
. 
-
(1) 连结
 ,求证:
,求证:  ;
;
-
(2) 求证:
 是
是  的切线;
的切线;
-
(3) 若
 ,
,  ,求
,求 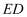 的值.
的值.
如图,点A、B是双曲线y=  上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=
上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=
 上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=
上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=
如图,一段河堤的斜坡BC=12m,为了加固河堤,需要将堤坝加厚竣工后,斜坡的坡度由原来1:2变成1:3.加固后斜坡AD的长是多少?

如图所示,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在  中,
中, 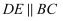 ,且
,且  把
把  分成面积相等的两部分.若
分成面积相等的两部分.若 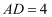 ,则
,则  的长为.
的长为.
 中,
中, 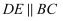 ,且
,且  把
把  分成面积相等的两部分.若
分成面积相等的两部分.若 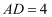 ,则
,则  的长为.
的长为. 
在平面直角坐标系中,点A,B的坐标分别为 、
、 , 点P的坐标为
, 点P的坐标为 .点E是y轴上一动点,QP⊥EP交AB于点Q(保持点Q在x轴上方),EF⊥EQ交AB于点F.
.点E是y轴上一动点,QP⊥EP交AB于点Q(保持点Q在x轴上方),EF⊥EQ交AB于点F.
 、
、 , 点P的坐标为
, 点P的坐标为 .点E是y轴上一动点,QP⊥EP交AB于点Q(保持点Q在x轴上方),EF⊥EQ交AB于点F.
.点E是y轴上一动点,QP⊥EP交AB于点Q(保持点Q在x轴上方),EF⊥EQ交AB于点F.
-
(1) 当PQ⊥AB时,求OE的长.
-
(2) 当点E在线段OB上移动时,设AQ=n,OE=m,求n关于m的函数表达式.
-
(3) 点E在射线OB上移动过程中,点Q、E、F构成的三角形与△OAB相似,求出点E的纵坐标.
反比例函数  与正比例函数
与正比例函数  在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
 与正比例函数
与正比例函数  在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( )
, 则河宽PT的长度是( )
 , 则河宽PT的长度是( )
, 则河宽PT的长度是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣  t2 , 飞机着陆至停下来共滑行( )
t2 , 飞机着陆至停下来共滑行( )
 t2 , 飞机着陆至停下来共滑行( )
t2 , 飞机着陆至停下来共滑行( )
A . 25米
B . 50米
C . 625米
D . 750米
先化简,再求代数式:  ÷(
÷(  ﹣x)的值,其中x=2sin 60°+2cos60°.
﹣x)的值,其中x=2sin 60°+2cos60°.
 ÷(
÷(  ﹣x)的值,其中x=2sin 60°+2cos60°.
﹣x)的值,其中x=2sin 60°+2cos60°.
如图1的风力发电机,风轮的三个叶片均匀分布,当风轮的叶片在风力作用下旋转时,最高点距地面 , 最低点距地面
, 最低点距地面 . 如图2是该风力发电机的示意图,发电机的塔身
. 如图2是该风力发电机的示意图,发电机的塔身 垂直于水平地面
垂直于水平地面 (点
(点 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  在同一平面内).
在同一平面内).
 , 最低点距地面
, 最低点距地面 . 如图2是该风力发电机的示意图,发电机的塔身
. 如图2是该风力发电机的示意图,发电机的塔身 垂直于水平地面
垂直于水平地面 (点
(点 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  在同一平面内).
在同一平面内).
-
(1) 求风轮叶片
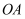 的长度;
的长度;
-
(2) 如图2,点
 在
在 右侧,且
右侧,且 . 求此时风叶
. 求此时风叶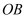 的端点
的端点 距地面的高度.(参考数据:
距地面的高度.(参考数据: ,
,  )
)
如图,△ABC中,∠ACB>∠ABC .

-
(1) 用直尺和圆规在∠ACB的内部作射线CM , 使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
-
(2) 若(1)中的射线CM交AB于点D , AB=9,AC=6,求AD的长.
直角△ABC中,∠C=90°,tan∠BAC= , 则sin∠ABC的值是( )
, 则sin∠ABC的值是( )
 , 则sin∠ABC的值是( )
, 则sin∠ABC的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图1),图2是侧面示意图.已知自动扶梯AC的坡度为i=1:2.4,AC=13m,BE是二楼楼顶,EF∥MN,B是EF上处在自动扶梯顶端C正上方的一点,且BC⊥EF,在自动扶梯底端A处测得B点仰角为42°.(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)


-
(1) 求二楼的层高BC约为多少米;
-
(2) 为了吸引顾客,开发商想在P处放置一个高10m的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出2m距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.
如图是由四个相同的正方体搭成的立体图形,其主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下面四个几何体中,从左面看是四边形的几何体有( )个.

A . 1个
B . 2个
C . 3个
D . 4个
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求  的值.
的值.
 的值.
的值.
如图,某河大堤上有一棵树ED,ED⊥CD,并且CD与水平地面AB平行,小明在A处测得树顶E的仰角为45°,然后沿着坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,求树ED的高度.(精确到1米)
(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01, =2.236)
=2.236)

为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )
(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)

A . 17.0米
B . 21.9米
C . 23.3米
D . 33.3米
最近更新
- 某同学按下列程序进行实验:指出Ⅰ、Ⅱ、Ⅲ处相应装置用到的合适仪器(填编号)a.圆底烧瓶 b.集气瓶 c.滴定管 d
- 若方程x2+x﹣1=0的两实根为α、β,那么下列说法不正确的是()A. α+β=﹣1 B. αβ=﹣1 C. α2+β2
- 下列实验操作正确的是 ()。 A.用100 mL容量瓶配制50 mL 0.1 m
- 从政治常识的角度看,漫画中现象的存在: A.损害了公民的基本政治权利B.破坏了公民与国家的和谐统一关系,应加以制止C.会
- He felt ________ that he should leave. A. strong B. stron
- 在2008年的诸多报刊杂志中经常出现”软实力”的概念。”软实力” 是同国家军事、经济力量等组成的“硬实力”相区别的一个概
- 依次填人下面句子中横线处的词语,正确的一项是(2分) ( ) ①那时候,他已经诗兴不作而研究志趣正浓。
- 求关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件.
- (三)阅读田晓菲《十三岁的际遇》(节选),完成11一13题。(10 分)①自从小心翼翼地佩带上那枚白色校徽起,北大就不再
- (6分)人体内苯丙氨酸的代谢途径如图所示。人群中,有若干种遗传病是由于苯丙氨酸的代谢缺陷所致,例如,苯丙氨酸的代谢产物之
- 下列各组元素属于p区的是() A.原子序数为1、2、7的元素 B.O、S、P C.Fe、Ar、Cl D.Na、Li、Mg
- 本单元中我们学习了很多概念,对于概念我们要在理解的基础上进行运用。 (1)由于 是保持物质化学性质的最小粒子,所
- 计算(-)2-1的结果是() A.- B.- C.- D.0
- 下列物质中属于还原性糖,能水解且最终产物为一种物质的是( ) A.葡萄糖 B.麦芽
- 面对激烈的国际竞争,中国企业必须走自主创新之路,尽快实现由“中国制造”到“中国智造”的转变。这一转变的实现,并不意味着企
- (本题10分)某班实行小组量化考核制.为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,
- 某同学用电流表和电压表来研究小灯泡在不同电压下的电功率.(1)他设计的实验电路如图所示,请你先用“×”将连接错误的导线标
- 地球大气层中二氧化碳含量不断增加的后果是 ( ) A.产生温室效应 B.产生酸雨露 C.污染环境
- 阅读理解D The deserts of the world are not all covered with s
- 图为东亚两个地区略图,读图回答下列各题。19.有关甲、乙两图的叙述,正确的是: A.甲图的比例尺较乙图大 B.①城市



