九年级(初三)数学下学期下册试题
如图, 这是一个由小立方体搭成的几何体的从上面看到的图形,小正方形中的数字表示该位置的小立方体的个数,请你画出它的从正面看和左面看所得到的图形。

如图,要使△ACD∽△ABC,只需添加条件(只要写出一种合适的条件即可).

已知k>0,那么函数y= 的图象大致是( )
的图象大致是( )
 的图象大致是( )
的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
反比例函数 (m为常数)当x<0时,y随x的增大而增大,则m的取值范围是( )
(m为常数)当x<0时,y随x的增大而增大,则m的取值范围是( )
 (m为常数)当x<0时,y随x的增大而增大,则m的取值范围是( )
(m为常数)当x<0时,y随x的增大而增大,则m的取值范围是( )
A . m<0
B .  C .
C .  D . m≥
D . m≥
 C .
C .  D . m≥
D . m≥
函数  是反比例函数,则a的值是( )
是反比例函数,则a的值是( )
 是反比例函数,则a的值是( )
是反比例函数,则a的值是( )
A . 1或﹣1
B . ﹣2
C . 2
D . 2或﹣2
点A(x1 , y1),B(x2 , y2)是反比例函数  的图象上两点,若0<x1<x2 , 则y1、y2的大小关系是.
的图象上两点,若0<x1<x2 , 则y1、y2的大小关系是.
 的图象上两点,若0<x1<x2 , 则y1、y2的大小关系是.
的图象上两点,若0<x1<x2 , 则y1、y2的大小关系是.
如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.

一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面和上面看到的形状图,该几何体最少要用________个立方块搭成,最多要用________个立方块搭成( )

A . 7,12
B . 8,11
C . 8,10
D . 9,13
如图,点  分别在
分别在  的边
的边  上,且
上,且  ,若
,若  ,则
,则  的长为。
的长为。
 分别在
分别在  的边
的边  上,且
上,且  ,若
,若  ,则
,则  的长为。
的长为。

如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则  的值为.
的值为.
 的值为.
的值为.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.

-
(1) 画出位似中心O;
-
(2) 求出△ABC与△A′B′C′的相似比.
sin60°的值等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

-
(1) 问题提出:如图1,在
 中,点
中,点 、
、 分别是
分别是 、
、 的中点,连接
的中点,连接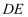 、
、 、
、 ,
,  与
与 交于点
交于点 , 若
, 若 , 则
, 则 ;
;
-
(2) 问题探究:如图2,在
 中,
中, ,
,  , 点
, 点 是
是 上一点(可与端点重合),连接
上一点(可与端点重合),连接 、
、 ,
,  , 求
, 求 面积的最小值;
面积的最小值;
-
(3) 问题解决:某湿地公园拟建一个梯形花园
 , 示意图如图3所示,其中
, 示意图如图3所示,其中 ,
,  ,
,  .管理员计划在
.管理员计划在 区域种植水生植物,在
区域种植水生植物,在 区域种植甲种花卉.根据设计要求,要满足点
区域种植甲种花卉.根据设计要求,要满足点 在
在 上,
上, ,
,  是锐角,且
是锐角,且 , 若种植水生植物每平方米需400元,种植甲种花卉每平方米需100元,求种植水生植物和种植甲种花卉所需总费用至少为多少元?
, 若种植水生植物每平方米需400元,种植甲种花卉每平方米需100元,求种植水生植物和种植甲种花卉所需总费用至少为多少元?
如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示.AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,  ≈1.414].
≈1.414].
 ≈1.414].
≈1.414]. 
如图,AB为⊙O的直径,C、D为⊙O上的两个点,  =
= 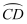 =
=  ,连接AD , 过点D作DE⊥AC交AC的延长线于点E .
,连接AD , 过点D作DE⊥AC交AC的延长线于点E .
 =
= 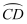 =
=  ,连接AD , 过点D作DE⊥AC交AC的延长线于点E .
,连接AD , 过点D作DE⊥AC交AC的延长线于点E . 
-
(1) 求证:DE是⊙O的切线.
-
(2) 若直径AB=6,求AD的长.
计算
-
(1)
 .
.
-
(2)
 .
.
有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚筒⊙A,⊙A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平面的距离CE为59cm.设AF∥MN.

-
(1) 求⊙A的半径长;
-
(2) 当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80cm,∠CAF=64°.求此时拉杆BC的伸长距离
(精确到1cm,参考数据:sin64°≈0.90,cos64°≈0.39,tan64°≈2.1)
在Rt△ABC中,∠C=90°,AB=4,BC=3,则cosB等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,且  =4,则
=4,则  =( )
=( )
 =4,则
=4,则  =( )
=( )
A .  B .
B .  C .
C .  D .
D . 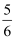
 B .
B .  C .
C .  D .
D . 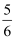
最近更新
- (2009年江苏生物)红豆杉是我国珍贵濒危树种。南京中山植物园于上世纪50年代从江西引进一些幼苗种植于园内。经过几十年的
- Fruit and vegetables can be grown nowadays _____. A.in what
- 人民币加快升值,已经并将继续对我国经济和人民生活产生影响。下列属于这一影响的有() ①有利于促进外贸出口发展方式的转变
- 2009年4月以来,从墨西哥蔓延开来的流感,最初被诊断为猪流感。后来,世界卫生组织等权威机构研究发现,这种流感病毒实际包
- 要除去下列4种物质中的少量杂质(括号内的物质为杂质) 甲:CaCO3(Na2CO3) 乙:NaOH
- 穆罕默德 阿里改革土地制度产生的主要作用是( ) A、废除了包税人的土地权 B、打击了宗教长老势力 C
- 下列对实验现象描述正确的是………………………………………………………( )A.硫在空气中燃烧生成二氧化硫
- Mr Black used to be busy.But now he'sretired and____,so he h
- — What do you think of the painting? Is it worth the money?
- 受西南气流和冷空气的影响,自5月7日夜开始,我省出现了今年以来的强降雨过程。此番强降雨对我省农作物生产和缓解旱情十分有利
- 我国作为一个发展中国家,多年来在致力于自身发展的同时,始终坚持不附带任何政治条件,向经济困难的其他发展中国家提供力所能及
- 我们中国人在人际交往中比较看重“实在”、“直来直去”、“实事求是”、“大恩不言谢”、“刀子嘴豆腐心”的价值。在西方,即使
- 智者学派有这样一段话:关于神,我不可能感受他们如何存在或如何不存在,我们 也不可能感知他们的形状和相貌是什么。因为有许多
- 阅读下面的文字,完成14━17题(18分)香山看叶郑云云站在幽静的山谷里,仰头望树,不见红叶。阳光应当在山外什么地方朗朗
- 计算:.
- ......
- 宁波市在2007年荣列“中国十大最具幸福感城市”。2008年5月的大型调查结果又表明,宁波市民的幸福指数高达98.8%。
- 如图所示的容器,其下部横截面积S2为上部横截面积Sl的3倍,当由管口注入重为G的某种液体时,上部液柱与容器的下部等高。则
- 设阿伏加德罗常数的值为NA。下列叙述正确的是 A.1.0L0.1mol/L的NH4Cl溶液中NH4+的个数为0.1NA
- 在下列物质中,属于人体内环境组成成分的是 A.DNA B.呼吸氧化酶 C.血红蛋白 D.



