九年级(初三)数学下学期下册试题
下列各图中,可以是一个正方体的平面展开图的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若反比例函数y=  (k≠0)的图象经过点(﹣1,2),则这个函数的图象一点经过( )
(k≠0)的图象经过点(﹣1,2),则这个函数的图象一点经过( )
 (k≠0)的图象经过点(﹣1,2),则这个函数的图象一点经过( )
(k≠0)的图象经过点(﹣1,2),则这个函数的图象一点经过( )
A . (﹣2,1)
B . (  ,2)
C . (﹣2,﹣1)
D . (
,2)
C . (﹣2,﹣1)
D . (  ,2)
,2)
 ,2)
C . (﹣2,﹣1)
D . (
,2)
C . (﹣2,﹣1)
D . (  ,2)
,2)
如图,△ABC中AB两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,且△A′B′C′与△ABC的位似比为2:1.设点B的对应点B′的横坐标是a,则点B的横坐标是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若双曲线y=  位于第二、四象限,则k的取值范围是( )
位于第二、四象限,则k的取值范围是( )
 位于第二、四象限,则k的取值范围是( )
位于第二、四象限,则k的取值范围是( )
A . k<1
B . k≥1
C . k>1
D . k≠1
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣2,2),B(﹣6,4),C(﹣4,8).

( 1 )画出△ABC关于x轴对称的△A1B1C1;
( 2 )以坐标原点O为位似中心,将△ABC缩小为原来的 , 得到
, 得到 , 使△ABC与
, 使△ABC与 位于位似中心两侧,请在平面直角坐标系中画岀
位于位似中心两侧,请在平面直角坐标系中画岀 ;
;
( 3 )设△ABC与△ 的周长分别为
的周长分别为 、
、 , 则
, 则 :
: = ▲ .
= ▲ .
如图是一个正方体的表面展开图,则原正方体中与建“字”所在的面相对的面上标的字是.

计算:2cos60°+4sin60°•tan30°﹣6cos245°.
如图1,图2分别是某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑竿DE、箱长BC拉杆AB的长度都相等,即DE=BC=AB=50,点B、F在线段AC上,点C在DE上,支杆DF=30cm.

-
(1) 若EC=36cm时,B,D相距48cm,试判定BD与DE的位置关系,并说明理由;
-
(2) 当∠DCF=45°,CF=
 AC时,求CD的长.
AC时,求CD的长.
如图,已知tanO= , 点P在边OA上,OP=5,点M、N在边OB上,PM=PN,如果MN=2,那么PM=.
, 点P在边OA上,OP=5,点M、N在边OB上,PM=PN,如果MN=2,那么PM=.
 , 点P在边OA上,OP=5,点M、N在边OB上,PM=PN,如果MN=2,那么PM=.
, 点P在边OA上,OP=5,点M、N在边OB上,PM=PN,如果MN=2,那么PM=. 
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径  ,扇形的圆心角
,扇形的圆心角  ,则该圆锥的母线长
,则该圆锥的母线长  为( )
为( )  .
.
 ,扇形的圆心角
,扇形的圆心角  ,则该圆锥的母线长
,则该圆锥的母线长  为( )
为( )  .
. 
A . 1
B . 12
C . 3
D . 6
在函数y=  (k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )
(k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )
 (k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )
(k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )
A . y1<y2<y3
B . y1<y3<y2
C . y3<y2<y1
D . y2<y3<y1
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.

计算或化简:
-
(1)
 ;
;
-
(2)
 .
.
已知点(-1,y1),(2,y2),(3,y3)在反比例函数y= 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
A . y1>y2>y3
B . y1>y3>y2
C . y3>y1>y2
D . y2>y3>y1
圆柱的侧面展开图形是( )
A . 圆
B . 矩形
C . 梯形
D . 扇形
如图是由5个相同的小立方块搭成的几何体,则下面四个平面图形中不是这个几何体的三视图的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,A,B两点分别在反比例函数 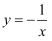 和
和  的图像上,连接OA,OB,若OA⊥OB,OB=2OA,则k的值为( )
的图像上,连接OA,OB,若OA⊥OB,OB=2OA,则k的值为( )
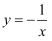 和
和  的图像上,连接OA,OB,若OA⊥OB,OB=2OA,则k的值为( )
的图像上,连接OA,OB,若OA⊥OB,OB=2OA,则k的值为( )

A . -2
B . 2
C . -4
D . 4
在Rt△ABC中,∠C=90°,下列各式中正确的是( )
A . sinA=sinB
B . tanA=tanB
C . sinA=cosB
D . cosA=cosB
计算:4cos30°+|3﹣ 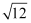 |﹣
|﹣  +(π﹣2018)0
+(π﹣2018)0
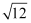 |﹣
|﹣  +(π﹣2018)0
+(π﹣2018)0
由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成 这个几何体的小立方体的个数是( )

A . 3
B . 4
C . 5
D . 6
最近更新
- You ______ regret all your life if you drive after you take
- 如图示根尖的结构及细胞分裂和分化的情况,下列有关叙述正确的是()A.观察细胞质壁分离时可选择a和b区细胞 B.观察根尖有
- 下列说法中体现存在决定思维的是( ) A.不怕做不到,就怕想不到 B.吾心便是宇宙,宇
- 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
- 图所示的种光学现象中,由于光的反射形成的是
- 2014年7月,某省物价局针对省内公办高校学费标准调整召开听证会,25名听证代表分别针对听证方案发表了意见。据悉,调整后
- 秦始皇曰:“天下共苦战斗不休,以有侯王,赖宗庙天下初定,又复立国,是树兵也,而求其宁息,岂不难哉!”秦始皇为解决上述问题
- (一)(12分)出师表诸葛亮宫中府中,俱为一体,陟罚臧否,不宜异同。若有作奸犯科及为忠善者,宜付有司论其刑赏,以昭陛下平
- 如图所示,是几种常用元件及其符号,请你在图中元件对应的空白处画出该元件的符号.
- 燕麦颖色受两对基因控制。用纯种黄颖与纯种黑颖杂交,F1全为黑颖,F1自交产生的F2中,黑颖黄颖白颖=1231。已
- 下图甲曲线表示某植物在恒温30℃时光合速率与光照强度的关系,图乙是某同学“探究影响植物光合速率的因素”的实验装置图(瓶中
- What does your sister do? She’s___________. She works for
- An 80-year-oldman was sitting on the sofa in his house along
- 如图为基因型AABb的某二倍体动物进行细胞分裂的某时期示意图.由此可知( )A.此细胞中的基因a是基因突变的结果
- 忠县为创建国家级绿色环保县城,污水处理厂决定购买10台污水处理设备,现有A,B两种型号的设备,已知购买1台A型号设备比购
- 下列关于科学方法和科学技术在经典实验和假说中运用的叙述,正确的是() A.孟德尔运用类比推理法,提出遗传的分离定律和自由
- 发射到宇宙中的同步卫星应与 ( ) A.地球自转的线速度相同 B.地球自转的角速
- 图中B为理想变压器,接在交变电压有效值保持不变的电源上.L为指示灯,灯泡L1和L2完全相同(其阻值均恒定不变),R是一个
- 小明在读一本书时,看到有这样一句话“天地虽大,但有一念向善,心存良知,虽凡夫俗子,皆可为圣贤。”说这句话的人是
- 4.下列各句中没有语病的一项是 A.一个人能否约束自己的言行,不但要靠严明的纪律,还要靠自己的品德修养。 B.多数大约十



