九年级(初三)数学下学期下册试题
如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.

-
(1) 指定路灯的位置(用点P表示);
-
(2) 在图中画出表示大树高的线段
-
(3) 若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树
如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为米.(结果保留两个有效数字)【参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601】

如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的序号是( )

 圆柱
圆柱  正方体
正方体  三棱柱
三棱柱  四棱锥
四棱锥
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,点O为坐标原点.已知反比例函数  的图象经A(﹣2,m),过点作AB⊥x轴.垂足为点B,且△OAB的面积为1.
的图象经A(﹣2,m),过点作AB⊥x轴.垂足为点B,且△OAB的面积为1.
 的图象经A(﹣2,m),过点作AB⊥x轴.垂足为点B,且△OAB的面积为1.
的图象经A(﹣2,m),过点作AB⊥x轴.垂足为点B,且△OAB的面积为1. 
-
(1) 求k和m的值;
-
(2) 点C(x,y)在反比例
 的图象上,当1≤x≤3时,求函数值y的取值范围.
的图象上,当1≤x≤3时,求函数值y的取值范围.
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: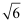 ≈2.449,结果保留整数)
≈2.449,结果保留整数)
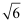 ≈2.449,结果保留整数)
≈2.449,结果保留整数)
|-1|-  -(5-π)0+4cos45°
-(5-π)0+4cos45°
 -(5-π)0+4cos45°
-(5-π)0+4cos45°
如图,小明用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,竹竿与旗杆相距22m,则旗杆的高为( )

A . 12m
B . 9.6m
C . 8m
D . 6.6m
如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

一个几何体的三种视图如图所示,则这个几何体是( )

A . 长方体
B . 圆锥
C . 圆台
D . 圆柱
反比例函数y1= ,y2=
,y2= (k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= .
(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= .
如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连结OB.点P为抛物线上AB上方的一个点,连结PA,作PQ⊥AB垂足为H,交OB于点Q.

-
(1) 求AB的长;
-
(2) 当∠APQ=∠B时,求点P的坐标;
-
(3) 当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.
如图,直线y=mx与双曲线y= 交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
 交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A . 2
B . m﹣2
C . m
D . 4
下图所示几何体是由7个完全相同的正方体组合而成,它的俯视图为( ).

A .  B .
B .  C .
C .  D .
D . 
 B .
B .
如图,二次函数 的图象与
的图象与 轴交于A,
轴交于A, 两点,与
两点,与 轴交于点
轴交于点 , 且关于直线
, 且关于直线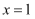 对称,点A的坐标为
对称,点A的坐标为 .
.
 的图象与
的图象与 轴交于A,
轴交于A, 两点,与
两点,与 轴交于点
轴交于点 , 且关于直线
, 且关于直线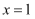 对称,点A的坐标为
对称,点A的坐标为 .
.
-
(1) 求二次函数的表达式;
-
(2) 连接
 , 若点
, 若点 在y轴上时,
在y轴上时, 和
和 的夹角为
的夹角为 , 求线段
, 求线段 的长度;
的长度;
-
(3) 当
 时,二次函数
时,二次函数 的最小值为
的最小值为 , 求
, 求 的值.
的值.
某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米,  =1.732).
=1.732).
 =1.732).
=1.732). 
A . 585米
B . 1014米
C . 805米
D . 820米
如图,在  中,∠BAC=90°,AD⊥BC,垂足为点D,下列结论错误的是( )
中,∠BAC=90°,AD⊥BC,垂足为点D,下列结论错误的是( )
 中,∠BAC=90°,AD⊥BC,垂足为点D,下列结论错误的是( )
中,∠BAC=90°,AD⊥BC,垂足为点D,下列结论错误的是( ) 
A . AB2=BD·BC
B . AC2=DC·BC
C . AD2=BD·DC
D . BC2=AB·AC
在市委市政府的领导下,经过全市人民的努力,义乌市获“全国文明城市”提名,为此小兵特制了一个正方体玩具,其展开图如图所示,正方体中与“全”字所在的面正对面上标的字是( )

A . 文
B . 明
C . 城
D . 国
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )

A . 10  海里
B . 10
海里
B . 10  海里
C . 10
海里
C . 10  海里
D . 20
海里
D . 20  海里
海里
 海里
B . 10
海里
B . 10  海里
C . 10
海里
C . 10  海里
D . 20
海里
D . 20  海里
海里
如图,在Rt△ABC中,∠C=90°,点D是AB的中点,点E是线段AC上的动点,BC=4,AB=8,当△ABC和△AED相似时,AE的长为.

-
(1) 解方程

-
(2) 计算

最近更新
- 若 ,,则 A. B. C. D.
- 1987年海峡两岸同胞38年的隔绝状态终于被打破的标志性事件是 A一国两制的出台
- .若=1-bi,其中a,b都是实数,i是虚数单位,则|a+bi|等于() A.
- 南昌大学研发的“硅衬底高光效GaN基蓝色发光二极管技术”获得2015年国家技术发明一等奖.请回答下列问题:(1)图甲是镓
- 正确表述下图中某海域的鱼密度、出海渔船数量、捕鱼量的是A.第2年后,若捕鱼量不变,鱼密度可以保持稳定 B.前4年中
- 下列实验操作正确的是() A. 点燃酒精灯 B. 滴加液体 C. 加热液体 D. 读取液体体积
- 2010年4月29日,上海世博会正式开幕。世博会于2010年5月1日至10月31日在上海举办。有242个国家和国际组织参
- 个体经济是以________为基础的所有制形式。 () A.劳动者自己劳动 B.社会统一劳
- 13.依次填入下列各句横线上的成语,与句意最贴切的一组是(3分)( ) ①无锡的梅园,面临太湖,以梅饰山,以山
- 如图,某简单几何体的正视图和侧视图都是边长为1的正方形,且其体积为,则该几何体的俯视图可以是().
- 设a,b,c是某三角形的三边长,T是该三角形的面积,证明a2+b2+c2≥T,并问何时取等号?
- 同步卫星是指相对于地面不动的人造地球卫星 A.它可以在地面任一点的正上方,且离地心的距离是一定的 B.它可以
- 在短文的空格内填入适当的词,使其内容通顺。每空格限填一词,首字母已给 At some time inyour life,
- 山东在半岛蓝色经济区建设中,注重突出海洋文化特色,发展蓝色文化产业,下大力气打造海洋文化品牌,推动文化与科技、旅游的融合
- 椭圆的左右焦点分别为,弦AB过,若的内切圆的周长为,A、B两点的坐标分别为和,则的值为( )。 A.
- 称取铜、锌混合物粉末10.0 g置于烧杯中,慢慢加入稀硫酸使其充分反应,直至固体质量不再减少为止,此时用去49.0 g稀
- 一定量混合气体在密闭容器中发生如下反应:xA(g)+yB(g) nC(g),达到平衡后,测得A气体的浓度为0.5mol
- ......
- (-2)2的算术平方根是
- As we all know, it’s not polite to keep others _________ for



