九年级(初三)数学下学期下册试题
计算: 

已知:如图①,在矩形ABCD中,AB=5,AD= 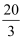 ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.

-
(1) 求AE和BE的长;
-
(2) 若将△ABF沿着射线BD方向平移,平移中的△ABF为△A1B1F1设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).
①当点F分别平移到线段AB上时,求出m的值
②当点F分别平移到线段AD上时,当直接写出相应的m的值.
-
(3)
如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AE交于点O,当∠A′BD=∠FAB时,请直接写出OB的长.

如图,某人在  处仰望山顶
处仰望山顶  ,测得仰角
,测得仰角  ,再往山的方向(水平方向)前进
,再往山的方向(水平方向)前进  至
至  处仰望山顶,测得仰角
处仰望山顶,测得仰角  .求这座山的高度(人的身高忽略不计). (参考数据:tan31º ≈
.求这座山的高度(人的身高忽略不计). (参考数据:tan31º ≈  , sin31º ≈
, sin31º ≈  , tan39º ≈
, tan39º ≈ 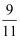 , sin39º ≈
, sin39º ≈ 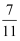 )
)
 处仰望山顶
处仰望山顶  ,测得仰角
,测得仰角  ,再往山的方向(水平方向)前进
,再往山的方向(水平方向)前进  至
至  处仰望山顶,测得仰角
处仰望山顶,测得仰角  .求这座山的高度(人的身高忽略不计). (参考数据:tan31º ≈
.求这座山的高度(人的身高忽略不计). (参考数据:tan31º ≈  , sin31º ≈
, sin31º ≈  , tan39º ≈
, tan39º ≈ 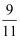 , sin39º ≈
, sin39º ≈ 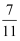 )
)
如图,在边长为1的小正方形网格中,点 、
、 、
、 、
、 都在这些小正方形的顶点上,AB、OD相交于点O,则
都在这些小正方形的顶点上,AB、OD相交于点O,则 ( )
( )
 、
、 、
、 、
、 都在这些小正方形的顶点上,AB、OD相交于点O,则
都在这些小正方形的顶点上,AB、OD相交于点O,则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,如果BC=4,sin∠DBC=  ,那么线段AB的长是.
,那么线段AB的长是.
 ,那么线段AB的长是.
,那么线段AB的长是. 
若两个相似三角形的面积比为2:3,那么这两个三角形的周长的比为( )
A . 4:9
B . 2:3
C .  :
: D . 3:2
D . 3:2
 :
: D . 3:2
D . 3:2
如图,  是等边三角形,延长
是等边三角形,延长  到点
到点  ,使
,使  ,连接
,连接  .若
.若  ,则
,则  的长为.
的长为.
 是等边三角形,延长
是等边三角形,延长  到点
到点  ,使
,使  ,连接
,连接  .若
.若  ,则
,则  的长为.
的长为. 
由7个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是()

A . 主视图的面积最大
B . 左视图的面积最大
C . 俯视图的面积最大
D . 三个视图的面积一样大
如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+ PB的最小值是.
PB的最小值是.
 PB的最小值是.
PB的最小值是.

用圆心角是216°,半径是5cm的扇形围成一个圆锥体的侧面(接缝处不重叠),则这个圆锥体的高是 cm.
如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点的对应点B′的横坐标是2,则点B的横坐标是 .

若函数  与
与 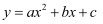 的图象如图所示,则函数
的图象如图所示,则函数  的大致图象为( )
的大致图象为( )
 与
与 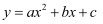 的图象如图所示,则函数
的图象如图所示,则函数  的大致图象为( )
的大致图象为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.

-
(1) 求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
-
(2) 除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.
利用我们数学课本上的计算器计算  sin52°, 正确的按键顺序是( )
sin52°, 正确的按键顺序是( )
 sin52°, 正确的按键顺序是( )
sin52°, 正确的按键顺序是( )
A .  B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=  的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=  ,OB=4,OE=2.
,OB=4,OE=2.
 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=  ,OB=4,OE=2.
,OB=4,OE=2. 
-
(1) 求反比例函数的解析式;
-
(2) 若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )

A .  =
= B .
B .  =
= C . ∠ABP=∠C
D . ∠APB=∠ABC
C . ∠ABP=∠C
D . ∠APB=∠ABC
 =
= B .
B .  =
= C . ∠ABP=∠C
D . ∠APB=∠ABC
C . ∠ABP=∠C
D . ∠APB=∠ABC
如图, 量具ABC是用来测量试管口直径的,AB的长为10cm,AC被分为60等份.如果试管口DE正好对着量具上20等份处(DE∥AB),那么试管口直径DE是 cm.
如图,矩形 中,E是
中,E是 的中点,
的中点, ,
,  , M是线段
, M是线段 上的动点,则
上的动点,则 的最小值是.
的最小值是.
 中,E是
中,E是 的中点,
的中点, ,
,  , M是线段
, M是线段 上的动点,则
上的动点,则 的最小值是.
的最小值是. 
一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:  1.414,
1.414,  =1.732).
=1.732).
 1.414,
1.414,  =1.732).
=1.732).

如图,在平面直角坐标系中,△ABC的边AB∥x轴,点A在双曲线y= (x<0)上,点B在双曲线y=
(x<0)上,点B在双曲线y= (x>0)上,边AC中点D在x轴上,△ABC的面积为8,则k= .
(x>0)上,边AC中点D在x轴上,△ABC的面积为8,则k= .

最近更新
- 下列关于实验现象的描述不正确的是 A.把铜
- 给小鼠注射一定剂量的胰岛素后,小白鼠进入休克状态,要使其复苏,可适量注射的物质是
- 我们生活中的很多现象,往往蕴涵了地理知识。下列现象与地球自转有关的是 ( ) A.盐城四季分明,春暖、夏热、秋凉、
- 下列各项中,不属于以为首的中共第一代领导人共同在社会主义改造和建设道路上的有益探索的是
- ,and the problem would be straightened out. A.A bit m
- Is this school ____ we visited three years ago?A. the one
- 实行按劳分配的前提是 A.生产资料公有制 B.社会主义条件下人们劳动的性质和特点C.社会主义公有制条件下生产力的发展
- 记承天寺夜游 苏 轼 元丰六年十月十二日夜,解衣欲睡,月色入户,欣然起行。念无与为乐者,遂至承天寺寻张怀民。怀民亦未寝,
- 比较下列三种物质,判断不正确的是()A.硬度最大的是金刚石 B.组成上都含碳元素 C.属于单质的是干冰 D.可用于实验室
- ---- Do you want to go to a movies? ---- _____A. N
- 基因型为AaBb (独立遗传)的一个初级精母细胞和一个初级卵母细胞分别产生的精子和卵细胞基因型的种类数比为 (不考虑交叉
- 淮安市汇通批发市场曾发生一场特大火灾。据查,火灾是由一个未熄灭的烟头引发的。那么未熄灭的烟头对发生这次特大火灾所起的作用
- 已知点,,点在直线上,求取得最小值时点的坐标。
- 已知两个羧基之间在浓硫酸作用下脱去一分子水生成酸酐,如: 某酯类化合物A是广泛使用的塑料增塑剂。A在酸性条件下能
- 某同学做了一个用以测定光照强度与生态系统稳定性关系的实验。将若干小球藻、水草及小鱼各一份(完全相同)放入甲、乙两个等同的
- 根据句子意思每空填一个英语单词 1.What’s this in E __________? 2.How do yo
- 1980年以来,黑龙江省西部水稻集中种植区向北推移了1个纬度左右,替代了原玉米种植区。引起这一变化的主要自然因素是()
- 如图是我们在观察某种细胞时使用的一些镜头,则下列有关说法错误的是() A.
- 结合文意,回答问题。 (1)蒋氏捕蛇十二年,“几死者数”,可他不以为“病”,反以为“幸”,这反映了他 什么样的心态?其中
- 下面是小东同学设计的骨的成份和特性的探究实验。项目 1号试管 2号试管 实验方法 用稀盐酸浸泡 用清水浸泡 鉴别结果 硬



