九年级(初三)数学下学期下册试题
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )

A .  B .
B .  C .
C .  D . 1
D . 1
 B .
B .  C .
C .  D . 1
D . 1
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A,B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
由7个相同的棱长为2的小立方块搭成的几何体如图所示.

-
(1) 请画出它从三个方向看到的形状图.
-
(2) 请计算几何体的表面积.
从-1,2,3,-6 这四个数中随机取两个数,分别记作 m,n,点(m,n)在函数 y= 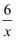
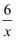
图象上的概率是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据:  ≈1.41,
≈1.41,  ≈1.73)
≈1.73)

如图所示,一次函数y=k1x+b与反比例函数y= (x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式k1x+b> 的解.
的解.
如图是每个面都标注了字母的立方体表面展开图.在展开前,与标注字母  的面相对的面上的字母为( )
的面相对的面上的字母为( )
 的面相对的面上的字母为( )
的面相对的面上的字母为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,交AB于点E,点F在AC上,DC=DF,若BC=3,EB=4,CD=x,CF=y,求y与x的函数关系式,并写出自变量x的取值范围.

一个几何体的三视图如图所示,则该几何体的形状可能是( )

A .  B .
B .  C .
C .  D .
D . 
用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:

-
(1) 直接写出a,b,c的值;
-
(2) 这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
-
(3) 当d=1,e=2,f=1时画出这个几何体的左视图.
如图,在平面直角坐标系中,直线 与比例函数
与比例函数 的图像交于
的图像交于 ,
,  两点,
两点, 为线段
为线段 的中点,连接
的中点,连接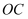 与反比例函数
与反比例函数 的图像交于点
的图像交于点 . 若
. 若 ,
,  , 则
, 则 的值为.
的值为.
 与比例函数
与比例函数 的图像交于
的图像交于 ,
,  两点,
两点, 为线段
为线段 的中点,连接
的中点,连接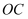 与反比例函数
与反比例函数 的图像交于点
的图像交于点 . 若
. 若 ,
,  , 则
, 则 的值为.
的值为.
如图是由五个相同的小正方体搭成的几何体,它的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若点(2,1)在双曲线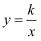 上,则k的值为 .
上,则k的值为 .
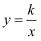 上,则k的值为 .
上,则k的值为 .
如图,点A在双曲线  上,连接
上,连接  ,作
,作  ,交双曲线
,交双曲线  于点B , 连接
于点B , 连接  .若
.若  ,则k的值为( )
,则k的值为( )
 上,连接
上,连接  ,作
,作  ,交双曲线
,交双曲线  于点B , 连接
于点B , 连接  .若
.若  ,则k的值为( )
,则k的值为( ) 
A . 1
B . 2
C .  D .
D . 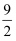
 D .
D . 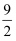
P是反比例函数y= 的图象上一点,过P点分别向x轴、y轴作垂线,所得的图中阴影部分的面积为6,则这个反比例函数的解析式为 ( )
的图象上一点,过P点分别向x轴、y轴作垂线,所得的图中阴影部分的面积为6,则这个反比例函数的解析式为 ( )
A . y=- B . y=
B . y=
C . y=-
C . y=- D . y=
D . y=
 B . y=
B . y=
C . y=-
C . y=- D . y=
D . y=
如图所示,一皮带轮的坡比是1:2.4,如果将货物从地面用皮带轮送到离地10米的平台,那么该货物经过的路程是 米.

已知:如图,  的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F.
的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F.
 的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F.
的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F. 
-
(1) 求证:BF是
 的切线;
的切线;
-
(2) 连接BC,若
 的半径为4,
的半径为4,  ,线段AD的长.
,线段AD的长.
已知点P(﹣2,﹣3)在反比例函数y= 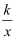 的图象上,当x≥﹣2时,y的取值范围是.
的图象上,当x≥﹣2时,y的取值范围是.
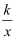 的图象上,当x≥﹣2时,y的取值范围是.
的图象上,当x≥﹣2时,y的取值范围是.
如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=  ,则该圆锥的侧面积是( )
,则该圆锥的侧面积是( )

A . 24  B . 24π
C . 16π
D . 12π
B . 24π
C . 16π
D . 12π
 B . 24π
C . 16π
D . 12π
B . 24π
C . 16π
D . 12π
如图,在平面直角坐标系中,四边形 的边
的边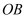 与x轴的正半轴重合,
与x轴的正半轴重合, ,
,  轴,对角线
轴,对角线 交于点M.已知
交于点M.已知 ,
,  的面积为4.若反比例函数
的面积为4.若反比例函数 的图象恰好经过点M,则k的值为.
的图象恰好经过点M,则k的值为.
 的边
的边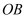 与x轴的正半轴重合,
与x轴的正半轴重合, ,
,  轴,对角线
轴,对角线 交于点M.已知
交于点M.已知 ,
,  的面积为4.若反比例函数
的面积为4.若反比例函数 的图象恰好经过点M,则k的值为.
的图象恰好经过点M,则k的值为.
最近更新
- 2015年10月13日,世界贸易组织支持了中国的申诉,要求美国在2016年4月1日前遵守WTO裁决,解决在反倾销和反补
- After school, he does homework _______ an hour every day.
- 1945年斯大林说,第二次世界大战与过去的战争不同,“不仅是占领一片土地,亦将其社会制度加诸其上”。战后体现这一言论的事
- 阅读说明文《“低头族”,你错过了什么》 “低头族”,你错过了什么 ①好莱坞动画大片《机器人总动员》中,描述了公元2700
- Last year the number of students who graduated with a drivin
- 我市干旱导致农作物生长发育不良,合理施用磷肥可提高其抗旱能力.下列化肥中属于磷肥的是()A. Ca(H2PO4)2 B.
- 2007年10月24日,我国第一颗探月卫星“ ”在西昌发射中心成功升空,我国因此跨入世界为数不多的具
- 2009年3月5日,温家宝总理在政府工作报告指出,过去一年,政府自身改革和建设取得了新的成绩,但与人民的期待仍有不小差距
- I have no idea ______ the journalist could have got his info
- 国家广电总局整顿“恶搞”文化,在社会产生强烈反响。有学者表示,一个国家、一个民族都以“恶搞”为能事,以群体狂欢和媒体追炒
- 下列句子的标点符号,使用不正确的一项是 A.“干什么呀!”他变了脸色,“你又不是老师,凭什么批评我?” B.对今年的城市
- “人肉搜索”是利用现代信息科技,变传统的网络信息搜索(机器搜索)为人找人、人问人的关系型网络社区
- 已知关于函数 (1)若此函数的图像与坐标轴只有个交点,求的值. (2)求证:关于的一元二次方程必有一个根是.
- “Helping survivors (生还者) of the earthquake and killer waves
- 中国传统文化重德治轻法治。而中国把依法治国和以德治国结合起来作为治国方略。这是因为 A只有抛弃传统文化,才能求得新发展
- 《德意志帝国宪法》与英国《权利法案》的不同在于 A.确立了君主立宪制 B.议会可
- He had a strange hairstyle andhe instantly became the _____
- 已知,如图,扇形中,,,若以为圆心,长为半径画弧交弧于点,过点作,垂足为,则图中阴影部分的面积为__________.
- 等质量的两块钠,第一块在足量氧气中加热,第二块在足量氧气(常温)中充分反应,则下列说法正确的是( )A.第一块钠
- ScarlettJohnasson developed ______ interest in acting at thr



