九年级(初三)数学下学期下册试题
如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )

A .  B . 20tan37°
C .
B . 20tan37°
C .  D . 20sin37°
D . 20sin37°
 B . 20tan37°
C .
B . 20tan37°
C .  D . 20sin37°
D . 20sin37°
计算:  .
.
 .
.
下列函数中,不是反比例函数的是( )
A . y= 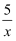 B . y=3x-1
C . y=
B . y=3x-1
C . y=  D . xy=
D . xy= 
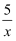 B . y=3x-1
C . y=
B . y=3x-1
C . y=  D . xy=
D . xy= 
下列几何体中从上面看到的图形是三角形的是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,△ABC的顶点是正方形网格的格点,则tanA的值为.

已知边长为8的正方形  截去一个角后成为五边形
截去一个角后成为五边形  ,点
,点  在线段
在线段  上,过点
上,过点  作
作  ,垂足为点
,垂足为点  ,过点
,过点  作
作  ,垂足为点
,垂足为点  ,
,  ,
,  ,设
,设  的长为
的长为  ,四边形
,四边形  的面积记为
的面积记为  .
.
 截去一个角后成为五边形
截去一个角后成为五边形  ,点
,点  在线段
在线段  上,过点
上,过点  作
作  ,垂足为点
,垂足为点  ,过点
,过点  作
作  ,垂足为点
,垂足为点  ,
,  ,
,  ,设
,设  的长为
的长为  ,四边形
,四边形  的面积记为
的面积记为  .
.

-
(1) 求
 ,
,  的长(分别用含
的长(分别用含  的代数式表示);
的代数式表示);
-
(2) 求
 关于
关于  的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
-
(3) 求四边形
 面积的最大值.
面积的最大值.
如图,在△ABC中,DE∥BC,若  ,那么
,那么  =( )
=( )
 ,那么
,那么  =( )
=( ) 
A .  B .
B . 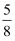 C .
C . 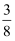 D .
D . 
 B .
B . 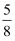 C .
C . 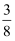 D .
D . 
如图,在矩形ABCD中,点F在AD上,射线BF交AC于点G,交CD的延长线于点E,则下列等式正确的为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:
-
(1)

-
(2)
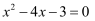
要制作两个形状相同的三角形框架,其中一个三角形的边长分别为8cm,10cm和12cm,另一个三角形的最短边长为2cm,则它的最长边为( )
A . 3cm
B . 4cm
C . 4.5cm
D . 5cm

-
(1) (提出问题)
如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
-
(2) (类比探究)
如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
-
(3) (拓展延伸)
如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
下列关于反比例函数  的说法不正确的是( )
的说法不正确的是( )
 的说法不正确的是( )
的说法不正确的是( )
A . 其图象经过点(-2,1)
B . 其图象位于第二、第四象限
C . 当x<0时,y随x增大而增大
D . 当x>-1时,y>2
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y= (x>0)和y=
(x>0)和y= (x>0)的图象于点P和Q,连接OP和OQ.则下列结论:
(x>0)的图象于点P和Q,连接OP和OQ.则下列结论:
①∠POQ可能等于90°;② =
= ; ③当K1+K2=0时,OP=OQ;④△POQ的面积是
; ③当K1+K2=0时,OP=OQ;④△POQ的面积是 (|k1+k2|).
(|k1+k2|).
其中一定正确的是( )

A . ①②
B . ②③
C . ①③
D . ①④
如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.

(参考数据:  ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
-
(1) 求点M到AB的距离;(结果保留根号)
-
(2) 在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数  (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为.
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为.
 (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为.
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为. 
如图,是一个几何体从三个方向看所得到的形状图.

-
(1) 写出这个几何体的名称;
-
(2) 画出它的一种表面展开图;
-
(3) 若从正面看长方形的高为
 ,从上面看三角形的边长为
,从上面看三角形的边长为 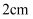 ,求这个几何体的侧面积.
,求这个几何体的侧面积.
如图,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则sin∠EAB的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.

-
(1) 求证:△CAD∽△CBA;
-
(2) 若BD=10,DC=8,求AC的长;
如图,在  中,
中, 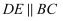 ,分别交
,分别交  ,
,  于点
于点  ,
,  .若
.若  ,
,  ,则
,则  的值为( )
的值为( )
 中,
中, 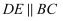 ,分别交
,分别交  ,
,  于点
于点  ,
,  .若
.若  ,
,  ,则
,则  的值为( )
的值为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,点A的坐标为  ,点D的坐标为
,点D的坐标为  ,若
,若  与
与  是位似图形,则
是位似图形,则  的值是( )
的值是( )
 ,点D的坐标为
,点D的坐标为  ,若
,若  与
与  是位似图形,则
是位似图形,则  的值是( )
的值是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 小李在图书馆看到一张纽约百老汇大街的老照片,只见电线横七竖八,拉得满街都是,即使是富人云集,基本上还见不到汽车。请你帮助
- 逻辑电路的信号有两种状态:一是高电位状态,用“1”表示;另一种是低电位状态,用“0”表示.关于这里的“1”和“0”下列说
- (4分)在我们生活的世界中,有各种形式的能源,如:煤炭、石油、太阳能、汽油。按照不同的划分,上述能源中属于一次能源的是_
- 下列变化属于化学变化的是() A. 菜刀生锈 B.瓷器破碎 C.干冰升华 D.滴水成冰
- 太平天国失败的原因,与中国历史上其他农民战争截然不同的是( )A.出现了战略上的失误 B.被中外反动势力联合镇压C
- 下列各句中,没有语病的一句是( ) A.南昌八一起义纪念馆里陈列着周恩来当年使用过的好多种东西。 B.阅读优秀的外
- 如图所示,四边形ABCD是平行四边形,∠D=120°,∠CAD=32°.则∠ABC、∠CAB的度数分别为( ) A
- 在如图的方格纸中,每个小正方形的边长都为l.(1)画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2;
- 豌豆的高茎基因(D)与矮茎基因(d)的根本区别是( ) A.分别控制显性和隐性性状
- 判断卵子是否受精的标志是( ) A.当卵黄膜和透明带的间隙可以观察到一个极体时 B.当卵黄膜和透明带的间隙可以观察到二
- 如图,∵∠A=∠D,∠B=∠E,∴△ABC∽△________.
- 一质量为6×103 kg的火箭从地面竖直向上发射,若火箭喷射燃料气体的速度(相对于火箭)为103 m/s,求: (1)每
- 以下正确反映我国新民主主义革命历程的是( ) A.五四运动 土地革命 国民革命 抗日战争 解放战争 新中国
- 2011年9月14日晚,备受各界瞩目的比尔·盖茨和巴菲特慈善晚宴在北京昌平拉斐特城堡庄园举行,且“巴比”信守此前承诺,并
- 某同学为研究热敏电阻RT(电阻值随温度的改变而改变,且对温度很敏感)的I-U关系,设计了如图甲所示的电路图,(1)该同学
- 中国历史上的丝绸之路是通往何地的商路? A.西亚和欧洲 B.东南亚 C.日本
- 科学家在研究大脑皮层某些区域(如图)时,发现它与躯体运动和语言活动功能有着密切的联系,下列叙述科学的是( )A.小
- — How was your trip to Hang Zhou, Jim?—Great! We ___ to Xixi
- 唐朝诗人岑参在《白雪歌送武判官归京》中写道:“中军置酒饮归客,胡琴琵琶与羌笛。”从岑参的诗句中,我们可以看出传统文化的特
- 分析下面的能量变化示意图,下列热化学方程式正确的是A.2A(g)+ B(g)=2C(g);△H=a kJ·mol-1(a



