九年级(初三)数学下学期下册试题
如图,马航370失联后,“海巡31”船匀速在印度洋搜救,当它行驶到A处时,发现它的北偏东 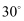 方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东
方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东  方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )
方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )
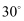 方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东
方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东  方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )
方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( ) 
A . 1小时
B . 2小时
C .  小时
D . 2
小时
D . 2  小时
小时
 小时
D . 2
小时
D . 2  小时
小时
如图,航拍无人机在  处测得正前方某建筑物顶部处
处测得正前方某建筑物顶部处  的仰角为45°,测得底部
的仰角为45°,测得底部  的俯角为31°.此时航拍无人机距地面
的俯角为31°.此时航拍无人机距地面  的高度为12米,求该建筑物的高度
的高度为12米,求该建筑物的高度  (结果保留整数).(参考数据:
(结果保留整数).(参考数据:  .)
.)
 处测得正前方某建筑物顶部处
处测得正前方某建筑物顶部处  的仰角为45°,测得底部
的仰角为45°,测得底部  的俯角为31°.此时航拍无人机距地面
的俯角为31°.此时航拍无人机距地面  的高度为12米,求该建筑物的高度
的高度为12米,求该建筑物的高度  (结果保留整数).(参考数据:
(结果保留整数).(参考数据:  .)
.) 
济南大明湖畔的“超然楼”被称作“江北第一楼”.某校数学社团的同学对超然楼的高度进行了测量.如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60米至B处,测得仰角为60°,若学生的身高忽略不计.

-
(1) 求∠ADB的度数;
-
(2) 求该楼的高度CD为多少米? (结果保留根号)
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为  ,AC=2,则sinB的值是().
,AC=2,则sinB的值是().
 ,AC=2,则sinB的值是().
,AC=2,则sinB的值是().
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,某地用图像记录了2月份某天24小时的温度随时间变化的情况,请你仔细观察图像,根据图中提供的信息,判断下列描述与图像不符合的是( )

A . 16时的温度约为1℃
B . 在-3℃以上的时间约为16小时
C . 温度是-1℃的时刻只有10时
D . 温度最低的时刻是4时
如图,在  中,
中,  ,
,  ,
, 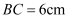 ,
,  是中线.点
是中线.点  从点
从点  出发以
出发以 
 中,
中,  ,
,  ,
, 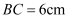 ,
,  是中线.点
是中线.点  从点
从点  出发以
出发以 
速度沿折线  匀速运动,到点
匀速运动,到点  停止运动.过点
停止运动.过点  作
作  ,垂足为点
,垂足为点  ,以
,以  为一边作矩形
为一边作矩形  ,且
,且  .点
.点  ,
,  始终位于
始终位于  的异侧,矩形
的异侧,矩形  与
与  的重叠部分面积为
的重叠部分面积为  ,点
,点  的运动时间为
的运动时间为  .
.

-
(1) 当点
 在边
在边  上时,
上时, 
 .
.
-
(2) 求
 与
与  之间的函数关系式.
之间的函数关系式.
-
(3) 当矩形
 与
与  的重叠部分为轴对称图形时,直接写出
的重叠部分为轴对称图形时,直接写出  的取值范围.
的取值范围.
为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据  ≈1.414.
≈1.414.  ≈1.732)
≈1.732)

如图,点E是正方形  边
边  上一点(点E不与
上一点(点E不与  重合),连接
重合),连接  交对角线
交对角线  于点F,
于点F,  的外接圆O交边
的外接圆O交边  于点G,连接
于点G,连接  、
、  ,设
,设  .
.
 边
边  上一点(点E不与
上一点(点E不与  重合),连接
重合),连接  交对角线
交对角线  于点F,
于点F,  的外接圆O交边
的外接圆O交边  于点G,连接
于点G,连接  、
、  ,设
,设  .
. 
-
(1) 求
 的度数.
的度数.
-
(2) 当
 时,求
时,求  .
.
-
(3) 用
 的代数式表示
的代数式表示  ,并说明理由.
,并说明理由.
如图,一条 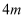 宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为
宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为  .
.
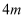 宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为
宽的道路将矩形花坛分为一个直角三角形和一个直角梯形,根据图中数据,可知这条道路的占地面积为  .
.
已知点  (-2,
(-2,  ),
),  (3,
(3,  )是反比例函数
)是反比例函数  图象上的两点,则有( )
图象上的两点,则有( )
 (-2,
(-2,  ),
),  (3,
(3,  )是反比例函数
)是反比例函数  图象上的两点,则有( )
图象上的两点,则有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,某教学楼AB的后面有一建筑物CD , 当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).
求教学楼AB的高度.(结果保留整数)
(参考数据:sin22°  0.37,cos22°
0.37,cos22°  0.93,tan22°
0.93,tan22°  0.40 .)
0.40 .)

图(1)是一个小正方形体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是

由若干个相同的小正方体搭成的一个几何体的俯视图如图,小正方形中的数字表示该位置的小正方体的个数,则这个几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:2sin45° 

如图是由一些相同的小正方体构成的立体图形的三视图。构成这个立体图形的小正方体的个数是( )
A . 3
B . 4
C . 5
D . 6
如图1所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.

-
(1) 【问题引入】
若点O是AC的中点,
 =
=  ,求
,求  的值;
的值;温馨提示:过点A作MN的平行线交BN的延长线于点G.
-
(2) 若点O是AC上任意一点(不与A,C重合),求证:
 •
•  •
•  =1;
=1;
-
(3)
【拓展应用】
如图2所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F,若
 =
=  ,
,  =
=  ,求
,求  的值.
的值.
如图是一个立体图形从左面和上面看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最少有个.

如图,在△ABC中,AC=8cm,BC=16cm,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?

先化简,再求代数式 的值,其中
的值,其中 .
.
 的值,其中
的值,其中 .
.
助推轮椅可以轻松解决起身困难问题.如图1是简易结构图,该轮椅前⊙O1和后轮⊙O2的半径分别为0.6dm和3dm,竖直连接处CO1=1dm,水平连接处BD与拉伸装置DE共线,BD=2dm,座面GF平行于地面且GF=DE=4.8dm,HF是轮椅靠背,∠ADE始终保持角度不变.初始状态时,拉伸杆AD的端点A在点B正上方且距地面2.2dm,则tan∠ADB的值为 .如图2,踩压拉伸杆AD,装置随之运动,当AD踩至与BD重合时,点E,F,H分别运动到点E',F',H',此时座面GF'和靠背F'H'连成一直线,点H运动到最高点H',且H',F,O2三点正好共线,则H'O2的长为 dm.

最近更新
- Beijing, the capital of China, is one of __________ cities i
- 在生物界,生物之间的_________是普遍存在的。正是由于________、_________和信息流的存在,使生物之
- 一束白光经三棱镜折射后,在光屏上形成自上而下为红、橙、黄、绿、蓝、靛、紫的色带,如图甲所示.若分别用红光和紫光平行于同一
- ΔABC中,分别是角A,B,C所对的边,且,则A=____________
- 细胞有丝分裂过程中,纺锤体形成于分裂期的A. 前期 B. 中期 C.后期
- 一直线与直二面角的两个面所成的角分别为α,β,则α+β满足 ( ) A. α+β<900
- 在现代市场经济中,政府越来越多地运用税收、利率等经济杠杆调节经济运行,经济杠杆能够起到调节作用的根本原因在于,它们 ()
- 下图表示在没有通风橱收集纯净的氯气时设计的装置图,图中A、B是可控制的弹簧铁夹。(1)烧杯中盛放的液体是________
- 下图为同学们经常使用的某品牌修正液包装标签上的部分文字和图片。清仔细阅读、观察,根据此图及日常生活经验分析、推测修正液的
- He is so shy that he often feels e____________ about making
- ---I’mgoing to buy a car. Any advice , Lily? ----Well, it
- 在等差数列{an}中,公差d=,前100项的和S100=45,则a1+a3+a5+…+a99=________.
- 水与人类的生活和生产密切相关,请回答下列问题:(1)图1是水通电分解的示意图,在实验过程中,观察到ab两试管中产生气体的
- 以下物质中含有氧分子的是 A、高锰酸钾 B、二氧化碳 C、液氧 D、________
- 下列评论中,不是直接针对“欧洲煤钢共同体”的是 A. “这样结合起来的联营生产意味着将来在法德之间发生战争是不可能的,
- 许多植物的果实和花瓣中含有色素。现提取几种植物的果实或花瓣的汁液,用稀酸、稀碱和水逐一检验,现象记录如下表。 植物的汁液
- 下列变化中,属于化学变化的是 A.汽油挥发 B.铜丝折弯 C.瓷碗破碎 D.纸张燃烧
- “一母生九子,连母十个样”是属于什么现象 ( )A.遗传B.变异C.生殖D.进化
- 2011年11月21日,国务院法制办公室公布《机关事务管理条例(征求意见稿)》,要求政府部门定期向社会公布公务接待费、公
- 惯性现象是非常普遍的,下列事例中利用了惯性的是:A.小型客车驾驶员驾车行驶时必须使用安全带;B.跳远运动员起跳前要助跑;



