九年级(初三)数学下学期下册试题
如图,是由几个相同的小正方体搭成的几何体,请你在图的右侧画出该几何体的俯视图.

已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB=  ,求BC的长.
,求BC的长.
 ,求BC的长.
,求BC的长.
如图,在△ABC中,∠ACB=90°,AC=BC,点D为边AC上一点,连接BD,作AH⊥BD的延长线于点H,过点C作CE∥AH与BD交与点E,连结AE并延长与BC交于点F,现有如下4个结论:①∠HAD=∠CBD;②△ADE∽△BFE;③CE·AH=HD·BE;④若D为AC中点,则  ,其中正确结论有( )个。
,其中正确结论有( )个。
 ,其中正确结论有( )个。
,其中正确结论有( )个。 
A . 1个
B . 2个
C . 3个
D . 4个
一个物体的俯视图是圆,这个物体的可能形状是、.
如图,在△ABC中,D、E分别是边BC、AC上的点,AD与BE相交于点F,若E为AC的中点,BD:DC=2:3,则AF:FD的值是 .

请同学们观察下图,要作出一个新图形,使新图形与原图形对应线段的比为2:1.
![]()
在Rt△ABC中,∠A=90°,AC=5,BC=13,那么tanB的值是( )
A . 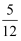 B .
B .  C .
C .  D .
D . 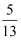
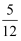 B .
B .  C .
C .  D .
D . 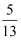
超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)

A . 253
B . 288
C . 206
D . 245
下列图形一定是相似图形的是( )
A . 两个矩形
B . 两个正方形
C . 两个直角三角形
D . 两个等腰三角形
一个几何体的三视图如图所示,则这个几何体的侧面积是( )

A . 4π
B . 2π
C . 4
D . π
如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.

如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE//AD交AC的延长线于E点.

-
(1) 求证:BE为⊙O的切线;
-
(2) 若AF=4CF,求tan∠E.
在A市建设规划图上,城区南北长为240cm,A市城区南北的实际长为18km,试写出该规划图的比例尺.
如图,测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量,测量船在A处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上,航行半个小时到达B点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD=海里(计算结果不取近似值).

在平面直角坐标系中,已知A( , 1),B(2,0),O(0,0),反比例函数y=
, 1),B(2,0),O(0,0),反比例函数y= 的图象经过点A.
的图象经过点A.
 , 1),B(2,0),O(0,0),反比例函数y=
, 1),B(2,0),O(0,0),反比例函数y= 的图象经过点A.
的图象经过点A.(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,点B与点D对应,试判断点D是否在该反比例函数的图象上.
反比例函数  ,在每个象限内,y随x的增大而增大,则m的取值范围是.
,在每个象限内,y随x的增大而增大,则m的取值范围是.
 ,在每个象限内,y随x的增大而增大,则m的取值范围是.
,在每个象限内,y随x的增大而增大,则m的取值范围是.
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB=米.

如图,在Rt△ABC中,∠B=90°,∠ACB=45°,∠D=30°,B、C、D在同一直线上,连接AD,若AB=  ,则sin∠CAD=.
,则sin∠CAD=.
 ,则sin∠CAD=.
,则sin∠CAD=. 
图1是一个闭合时的夹子,图2是该夹子的侧面简化示意图,夹子两边为AC , BD (闭合时点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E , OF⊥BD于点F , OE=OF=1cm,AC=BD=6cm,CE=DF , CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.

-
(1) 当E , F两点的距离最大时,求∠EOF增加了多少度(结果精确到1°,参考数据:
tan67.4°≈2.40,tan15.5°=0.278,tan74.5°≈3.60):
-
(2) 当夹子的开口最大(即点C与点D重合)时,求A , B两点间的距离.
如图所示是五个大小完全相同的小正方体搭成的几何体,则从左面看到的几何体的形状图为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 题目:爱在细微处 要求:(1)写一篇600字左右的文章。 (2)不得透露个人相关信息。 (3)不得抄袭。
- (10分)32.5g锌可以跟150g硫酸溶液恰好完全反应。计算:① 可制得氢气多少克?把溶液蒸干,得到多少克硫酸锌?②
- 如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足, AC=BC. ⑴求证:CD=BE.⑵若AD=3
- 某校初三年级有两个班,在一次数学测验中,一班50人的平均分是82分,二班45人的平均分是80分,则这次测验全级的平均分是
- (4分)标准状况下,22.4LHCl气体溶于50mL水再配制成250mL溶液,(1)求所得盐酸的物质的量浓度?(2)若将
- U、V、W、X、Y、Z是原子序数依次增大的六种短周期元素。U的单质在W2中燃烧可生成UW和UW2两种气体。X的单质是一种
- 如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C. (1)由∠CBE=∠A可以判断______∥______,
- 李约瑟说:“每当人们在中国的文献中查找一种具体的科技史料时,往往会发现它的焦点在宋代,不管在应用科学方面或纯粹科学方面都
- 17、下列划线成语的使用全都正确的一组是( )(3分) ①刘小玉教授上课时旁征博引,还不时夹着所引史料的
- 现有四种短周期元素X、Y、Z、W,其中:① X、W原子的电子层数与最外层电子数之比分别为3:1和 1:3② Y原子是元素
- 《名人传》是《语文课程标准》推荐的课外读物,根据你对这部名著的阅读,回答以下两个问题。 ①这部名著是法国著名作家
- 有人对“打的”现象做过一个形象的描述:青年人没钱也“打的”,中年人有钱才“打的”,老年人有钱也不“打的”,这主要反映了(
- 元素周期表是学习和研究化学的重要工具。下表是元素周期表的部分信息:1H 氢 2He 氦 3Li 锂 4Be 铍 5B 硼
- 广西壮族自治区大化瑶族自治县盛产的大化奇石,以其独特的收藏价值深受奇石收藏家的喜爱。随着奇石资源逐渐枯竭,近两年来,大化
- 给下列加粗的字注音。(4分) 炫耀() 称职() 滑稽()
- 在狗的精巢中,由A、T、C 三种碱基参与构成的核苷酸共有X种;其DNA分子结构稳定性最低的时期在细胞周期的Y期;DNA复
- 2015年8月15日,苏宁易购正式启动送货准时性、退款及时性和退换货效率三大服务保障项目。只要消费者在苏宁易购购物,以订
- 已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99,求他的总分和平均成绩的一个算法为: 第一步 取A=89,B
- 近年来,我国多地出现雾霾天气增多现象,下列不属于大气污染物的是 A.可吸入颗粒物(PM2.5)
- 下列物质中一定属于氧化物的是() A.含有氧元素的化合物 B.能分解出氧气的化合物 C.氧气跟某种物质反应的生成物 D.



