九年级(初三)数学：上学期上册　　 下学期下册

九年级(初三)数学下学期下册试题

已知反比例函数y= $\text{[math]}$ （a≠0），当x＞0时，它的图象y随x的增大而减小，那么二次函数y=ax²﹣ax的图象只可能是（　　）

A .

B .

C .

D .

已知由几个大小相同的小立方块搭成的几何体，从上面观察，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请分别画出从正面、左面看到的这个几何体的形状图（几何体中每个小立方块的棱长都是1cm）画图时要用刻度尺．

如图是由四个大小相同的立方体组成的几何体，则这个几何体的左视图是（）

A .

B .

C .

D .

一个圆锥的底面半径长是2，母线长是3，则这个圆锥侧面展开图形的面积为．

如图，

中，

厘米，

厘米，点

从

出发，以每秒

厘米的速度向

运动，点

从

同时出发，以每秒

厘米的速度向

运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以

、

为顶点的三角形与

相似时，运动时间是多少？

有一块直角边AB=3cm，BC=4cm的Rt△ABC的铁片，现要把它加工成一个正方形（加工中的损耗忽略不计），则正方形的边长为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

定义：有一组邻角相等，对角线相等，且对边不相等的凸四边形叫做“等邻对角四边形”，如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，四边形 $\text{[math]}$ 即为“等邻对角四边形”．

（1）概念理解
①如图2，在等边 $\text{[math]}$ 中， $\text{[math]}$ ，点D，E分别在 $\text{[math]}$ 上， $\text{[math]}$ ，当 $\text{[math]}$ 的长为时，四边形 $\text{[math]}$ 为“等邻对角四边形”．
②如图3，在 $\text{[math]}$ 中，点E，D在 $\text{[math]}$ 上，点F在 $\text{[math]}$ 上， $\text{[math]}$ ，四边形 $\text{[math]}$ 为“等邻对角四边形”，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．
（2）性质探究
根据图1及其条件，探究 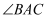$\text{[math]}$ 与 $\text{[math]}$ 的数量关系．
（3）问题解决
如图4，在“等邻对角四边形” $\text{[math]}$ 中， $\text{[math]}$ 与 $\text{[math]}$ 的延长线相交于点E．若 $\text{[math]}$ ，求 $\text{[math]}$ 的长，并指出 $\text{[math]}$ 的度数是否可以等于90°，不必说明理由．

已知反比例函数y＝ $\text{[math]}$ 的图象经过点(3，2)，那么下列四个点中，也在这个函数图象上的是（）

A . (3，－2) B . (－2，－3) C . (1，－6) D . (－6，1)

函数 $\text{[math]}$ 与 $\text{[math]}$ 在同一直角坐标系中的图象大致是下图中的（）

A .

B .

C .

D .

某长江大桥采用低塔斜拉桥桥型(如甲图)，图乙是从图甲引申出的平面图，假设你站在桥上测得拉索AB与水平桥面的夹角是30°，拉索BD与水平桥面的夹角是60°，两拉索底端距离AD＝20米，则立柱BC的高为（）

A . 20 $\text{[math]}$ 米 B . 10米 C . 10 $\text{[math]}$ 米 D . 20米

如图是百度地图的一部分（比例尺1：4000000）．按图可估测杭州在嘉兴的南偏西　　度方向上，杭州到嘉兴的图上距离约2cm，则杭州到嘉兴的实际距离约为．

如图，在△ABC中，∠ACB＝90º，CD⊥AB，BC＝1.

（1）如果∠BCD＝30º，求AC；
（2）如果tan∠BCD＝ $\text{[math]}$ ，求CD.

若两个三角形全等.则这两个三角形的相似比为.

如图，点M在BC上，点N在AM上，CM=CN， $\text{[math]}$ ，下列结论正确的是（　　）

A . △ABM∽△ACB B . △ANC∽△AMB C . △ANC∽△ACM D . △CMN∽△BCA

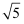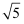我校兴趣小组同学为测量校外“御墅临枫”的一栋电梯高层AB的楼高，从校前广场的C处测得该座建筑物顶点A的仰角为45°，沿着C向上走到30 $\text{[math]}$ 米处的D点．再测得顶点A的仰角为22°，已知CD的坡度：i=1：2，A、B、C、D在同一平面内，则高楼AB的高度为（　　）（参考数据；sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）

A . 60 B . 70 C . 80 D . 90

如图，点E是矩形ABCD的边AD的中点，且BE⊥AC于点F，则下列结论中错误的是（）

A . AF＝ $\text{[math]}$ CF B . ∠DCF＝∠DFC C . 图中与△AEF相似的三角形共有5个 D . tan∠CAD＝ $\text{[math]}$

一司机驾驶汽车从甲地去乙地，他以80千米/时的平均速度用了6小时到达目的地，当他按原路匀速返回时，汽车的速度v（千米/时）与时间t（小时）的函数关系为（　　）

A . v＝ $\text{[math]}$ B . v+t＝480 C . v＝ $\text{[math]}$ D . v＝ $\text{[math]}$

如图，某小区有甲、乙两座楼房，楼间距BC为50米，在乙楼顶部A点测得甲楼顶部D点的仰角为37°，在乙楼底部B点测得甲楼顶部D点的仰角为60°，则甲、乙两楼的高度分别为多少？(结果精确到1米，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\text{[math]}$ ≈1.73)

在平面直角坐标系中，O为原点，点 $\text{[math]}$ ，点C在y轴的正半轴上， $\text{[math]}$ ．

（1）如图①，求点C的坐标；
（2）将 $\text{[math]}$ 沿x轴向右平移得 $\text{[math]}$ ，点A ， O ， C的对应点分别为 $\text{[math]}$ ．设 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分的面积为S ．
①如图②，当 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分为四边形时， $\text{[math]}$ 分别与 $\text{[math]}$ 相交于点D ， E ，试用含有t的式子表示S ，并直接写出t的取值范围；

②当S取得最大值时，求t的值（直按写出结果即可）．

如图，已知AB∥CD，若 $\text{[math]}$ ，则 $\text{[math]}$ =．

九年级(初三)数学： 上学期上册 下学期下册

九年级(初三)数学下学期下册试题

九年级(初三)数学：上学期上册　　下学期下册