九年级(初三)数学下学期下册试题
图中的阴影部分是某水库大坝横截面,小明站在大坝上的A处看到一棵大树CD的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面的夹角为60°,在A处测得树顶D的俯角为15°,如图所示,已知斜坡AB的坡度i=  :1,若大树CD的高为8
:1,若大树CD的高为8  米,则大坝的高为( )米(结果精确到1米,参考数据≈1.414
米,则大坝的高为( )米(结果精确到1米,参考数据≈1.414  ≈1.732)
≈1.732)
 :1,若大树CD的高为8
:1,若大树CD的高为8  米,则大坝的高为( )米(结果精确到1米,参考数据≈1.414
米,则大坝的高为( )米(结果精确到1米,参考数据≈1.414  ≈1.732)
≈1.732) 
A . 18
B . 19
C . 20
D . 21
如图,反比例函数  (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6)。若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是。
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6)。若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是。
 (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6)。若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是。
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6)。若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是。
一个圆锥的底面半径r=6,母线l=10,则这个圆锥的侧面积是
小明在测量楼高时,先测出楼房落在地面上的影长BA为15米,如图所示,然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )

A . 10米
B . 12米
C . 15米
D . 22.5米
如图,身高为1.6米的小华站在离路灯灯杆8米处测得影长2米,则灯杆的高度为米.

下面的几何体中,主视图为三角形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.

如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,E、F分别为AB、AC上的点,沿直线EF将∠B折叠,使点B恰好落在BC上的D处,当△ADE恰好为直角三角形时,BE的长为 .

如图,正方形ABOC的边长为2,反比例函数  的图象过点A,则k的值是( )
的图象过点A,则k的值是( )
 的图象过点A,则k的值是( )
的图象过点A,则k的值是( )
A . 2
B . ﹣2
C . 4
D . ﹣4
如图,已知  ABC的三个顶点的坐标分别为A(−1,2)、B(−3,0)、C(0,0).
ABC的三个顶点的坐标分别为A(−1,2)、B(−3,0)、C(0,0).
 ABC的三个顶点的坐标分别为A(−1,2)、B(−3,0)、C(0,0).
ABC的三个顶点的坐标分别为A(−1,2)、B(−3,0)、C(0,0).

-
(1) 请直接写出点A关于x轴对称的点
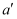 的坐标;
的坐标;
-
(2) 以C为位似中心,在x轴下方作
 ABC的位似图形△A1B1C1 , 使放大前后位似比为1:2,请画出图形,并直接写出
ABC的位似图形△A1B1C1 , 使放大前后位似比为1:2,请画出图形,并直接写出  A1B1C1的面积= ;
A1B1C1的面积= ;
-
(3) 请直接写出:以A,B,C,D为顶点的平行四边形的第四个顶点D的坐标.
如图,  ,则下列结论不成立的是( )
,则下列结论不成立的是( )
 ,则下列结论不成立的是( )
,则下列结论不成立的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
使用计算器求下列三角函数值(精确到0.0001):
(1)sin71°24′
(2)cos54°21′18″
(3)tan21°17′23″.
把三角形三边的长度都扩大为原来的2倍,则锐角A的正弦函数值
A . 扩大为原来的2倍
B . 缩小为原来的 C . 不变
D . 不能确定
C . 不变
D . 不能确定
 C . 不变
D . 不能确定
C . 不变
D . 不能确定
一个圆锥的底面半径为3,母线长为5,则圆锥的侧面积是( )
A . 9π
B . 18π
C . 15π
D . 27π
如图, , 且
, 且 ,
,  ,
,  , 则
, 则 的长度为.
的长度为.
 , 且
, 且 ,
,  ,
,  , 则
, 则 的长度为.
的长度为.
两个相似三角形的面积之比为4:25,则这两个三角形的周长比为.
已知正比例函数y1=x,反比例函数 , 由y1 , y2构造一个新函数y=x+
, 由y1 , y2构造一个新函数y=x+ , 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
, 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
 , 由y1 , y2构造一个新函数y=x+
, 由y1 , y2构造一个新函数y=x+ , 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
, 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:①该函数的图象是中心对称图形;
②当x<0时,该函数在x=﹣1时取得最大值﹣2;
③y的值不可能为1;
④在每个象限内,函数值y随自变量x的增大而增大.
其中正确的命题是( )

A . ①②④
B . ①②③
C . ②③
D . ①③
图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为70°时,箱盖ADE落在AD′E′的位置(如图2所示).已知AD=60厘米,DC=40厘米,求点D' 到BC的距离.
(参考数据:sin70°≈0.94,cos70°≈0.34)

如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3  米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )

A . 5米
B . 6米
C . 8米
D . (3+  )米
)米
 )米
)米
如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有( )

A . 1对
B . 2对
C . 3对
D . 4对
最近更新
- The pale face of my friend suggested that he ______ in poor
- 认识具有反复性和无限性,追求真理是一个永无止境的过程。认识的这些特点告诉我们应该( ) ①在实践中认识和发现真
- 如图所示,一只小球悬挂在弹簧的下端.现用手将小球向下拉一小段位移后释放,便可看到小球做上下的振动.当小球振动到达最高点时
- 一James didn’t show up last night, did he? 一No.He __________.
- 下列词语中加点字的注音,完全正确的一项是( ) A.牟取(móu) 叱咤(zhà) 匀称(chèn)
- (4分)一幢六层大楼,相邻两层楼窗台之间的距离都是3m,现从第三层楼窗台把一个物体竖直向上抛出,它最高可达到第六层楼窗台
- 病毒生活的环境是 A.土壤 B.活的细胞中 C.空气中 D.水中
- 阅读下面文言文,完成文后各题。 曾文正公①与左季高②相国同乡,相友善,叉属姻亲。粤逆猖獗.蔓延几遍天下,公与左相戮力讨贼
- 用来测定空气成分的方法很多,图1所示的是小明用红磷在空气中燃烧的测定方法。实验过程是:图1 第一步:将集气瓶容积划分为五
- 在磁感强度为0.48T的匀强磁场中,有一个长为20cm、宽为10cm的矩形线圈。则穿过线圈平面的磁通量最大值为_____
- Many computer games _______ a lot of violence anddo teenage
- 20世纪60年代中期,法国戴高乐政府提出了“缓和、谅解、合作”的对苏外交策略,同苏联进行合作达成缓和;60年代末70年
- 古代青铜艺术进入繁荣时期应是在 A.商周时代 B.秦汉时期 C.南北朝时期 D.隋唐时
- Hotel Icaria Barcelona Hotel Location Hotel Icaria Barcelona
- 12. --- Are you familiar ___ the music ? --- Yes. The mus
- The museum is ___ far ____ it will take us half an hour to g
- 随着改革的不断深入,我国政府的管理方式正在发生积极变化。以北京为例:京广中心附近道路塌陷时,许多人次日一早便收到市政府发
- 以“假如我处在 的位置上”为话题,自拟题目,写一篇不少于800字的作文。
- X、Y、Z、W有如图所示的转化关系,则X、W可能是 ①C、O 2 ②AlCl 3 、NaOH ③Fe、HNO 3 ④S、
- The man founded a university named himself, and his b



