九年级(初三)数学下学期下册试题
如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道  .无人机从点A的正上方点C , 沿正东方向以
.无人机从点A的正上方点C , 沿正东方向以  的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
 .无人机从点A的正上方点C , 沿正东方向以
.无人机从点A的正上方点C , 沿正东方向以  的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.
的速度飞行15s到达点D , 测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E , 测得点B的俯角为37°.

(参考数据:  ,
,  ,
,  ,
, 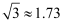 )
)
-
(1) 求无人机的高度
 (结果保留根号);
(结果保留根号);
-
(2) 求
 的长度(结果精确到1m).
的长度(结果精确到1m).
如图,在△ABC中,AB=AC=1,BC=  ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
-
(1) 通过计算,判断AD2与AC•CD的大小关系;
-
(2) 求∠ABD的度数.
若反比例函数y= 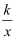 (k≠0)的图象经过点P(﹣2,3),则该函数的图象
(k≠0)的图象经过点P(﹣2,3),则该函数的图象  的点是( )
的点是( )
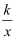 (k≠0)的图象经过点P(﹣2,3),则该函数的图象
(k≠0)的图象经过点P(﹣2,3),则该函数的图象  的点是( )
的点是( )
A . (3,﹣2)
B . (1,﹣6)
C . (﹣1,6)
D . (﹣1,﹣6)
我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b的反比例函数,其函数关系式可以写为a=  (S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:;函数关系式:.
(S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:;函数关系式:.
 (S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:;函数关系式:.
(S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:;函数关系式:.
已知:点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)是函数y=- 图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
 图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
A . y1<y2<y3
B . y2<y3<y1
C . y3<y2<y1
D . 无法确定
如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(﹣1,2),(3,2),点B在x轴上,点B的坐标为(3,0),抛物线y=﹣x2+bx+c经过A、C两点.

-
(1) 求该抛物线所对应的函数关系式;
-
(2) 点P是抛物线上的一点,当S△PAB=
 S△ABC时,求点P的坐标;
S△ABC时,求点P的坐标;
-
(3) 若点N由点B出发,以每秒
 个单位的速度沿边BC、CA向点A移动,
个单位的速度沿边BC、CA向点A移动,  秒后,点M也由点B出发,以每秒1个单位的速度沿线段BO向点O移动,当其中一个点到达终点时另一个点也停止移动,点N的移动时间为t秒,当MN⊥AB时,请直接写出t的值,不必写出解答过程.
秒后,点M也由点B出发,以每秒1个单位的速度沿线段BO向点O移动,当其中一个点到达终点时另一个点也停止移动,点N的移动时间为t秒,当MN⊥AB时,请直接写出t的值,不必写出解答过程.
一个面积为42的长方形,其相邻两边长分别为x和y,请你写出与之间的函数解析式,并画出其图象.
一个立体图形由4个相同的正方体组成,如果从左面看到的图形如图所示,那么这个立体图形不可能是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
风能作为一种清洁能源越来越受到世界各国的重视,我省多地结合自身地理优势架设风力发电机利用风能发电.王芳和李华假期去大理巍山游玩,看见风电场的各个山头上布满了大大小小的风力发电机,好奇的想知道风力发电机塔架的高度.如图,王芳站在坡度  ,坡面长
,坡面长  的斜坡
的斜坡  的底部
的底部  点测得
点测得  点与塔底
点与塔底  点的距离为
点的距离为  ,此时,李华在坡顶
,此时,李华在坡顶  点测得轮毂
点测得轮毂  点的仰角
点的仰角  ,请根据测量结果帮他们计算风力发电机塔架
,请根据测量结果帮他们计算风力发电机塔架  的高度.(结果精确到
的高度.(结果精确到  ,参考数据
,参考数据  ,
,  ,
,  ,
,  ,
, 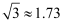 )
)
 ,坡面长
,坡面长  的斜坡
的斜坡  的底部
的底部  点测得
点测得  点与塔底
点与塔底  点的距离为
点的距离为  ,此时,李华在坡顶
,此时,李华在坡顶  点测得轮毂
点测得轮毂  点的仰角
点的仰角  ,请根据测量结果帮他们计算风力发电机塔架
,请根据测量结果帮他们计算风力发电机塔架  的高度.(结果精确到
的高度.(结果精确到  ,参考数据
,参考数据  ,
,  ,
,  ,
,  ,
, 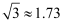 )
) 
如图,一次函数  的图象与
的图象与  轴相交于点
轴相交于点  ,与
,与  轴交于点
轴交于点  ,点
,点  为
为  轴上一点,点
轴上一点,点  为
为  第二象限图象上的动点,过点
第二象限图象上的动点,过点  ,
,  作直线
作直线  交线段
交线段 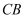 于点
于点  ,连接
,连接  ,
,  ,若
,若  ,则
,则  的坐标为.
的坐标为.
 的图象与
的图象与  轴相交于点
轴相交于点  ,与
,与  轴交于点
轴交于点  ,点
,点  为
为  轴上一点,点
轴上一点,点  为
为  第二象限图象上的动点,过点
第二象限图象上的动点,过点  ,
,  作直线
作直线  交线段
交线段 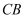 于点
于点  ,连接
,连接  ,
,  ,若
,若  ,则
,则  的坐标为.
的坐标为.

计算:20130﹣  +2cos60°+(﹣2)
+2cos60°+(﹣2)
 +2cos60°+(﹣2)
+2cos60°+(﹣2)
如图,是小亮晚上在广场散步的示意图,图中线段  表示站立在广场上的小亮,线段
表示站立在广场上的小亮,线段  表示直立在广场上的灯杆,点P表示照明灯的位置.
表示直立在广场上的灯杆,点P表示照明灯的位置.
 表示站立在广场上的小亮,线段
表示站立在广场上的小亮,线段  表示直立在广场上的灯杆,点P表示照明灯的位置.
表示直立在广场上的灯杆,点P表示照明灯的位置. 
-
(1) 在小亮由B处沿
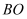 所在的方向行走到达O处的过程中,他在地面上的影子长度越来越(用“长”或“短”填空);请你在图中画出小亮站在
所在的方向行走到达O处的过程中,他在地面上的影子长度越来越(用“长”或“短”填空);请你在图中画出小亮站在  处的影子
处的影子  ;
;
-
(2) 当小亮离开灯杆的距离
 时,身高为
时,身高为  的小亮的影长为
的小亮的影长为  ,
, ①灯杆的高度为多少m?
②当小亮离开灯杆的距离
 时,小亮的影长变为多少m?
时,小亮的影长变为多少m?
如图,在平面直角坐标系中,已知点A(3,0),点B(0,-4),则tan∠OAB的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣  的图象上,则y1 , y2 , y3的大小关系是.
的图象上,则y1 , y2 , y3的大小关系是.
 的图象上,则y1 , y2 , y3的大小关系是.
的图象上,则y1 , y2 , y3的大小关系是.
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.

-
(1) 求证:△DCE∽△BCA;
-
(2) 若AB=3,AC=4.求DE的长.
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.

-
(1) 求证:△ADE∽△ABC;
-
(2) 若AD=3,AB=5,求
 的值.
的值.
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(如∠O)为60°,A,B,C,D都在格点上,且线段AB、CD相交于点P,则tan∠APC的值是

学好数学,就是为能更好解决生活中遇到的问题,如图所示,为了测量山的高度AC,在水平面E处测得山顶A的仰角为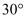 ,
,  , 自E沿着EC方向向前走
, 自E沿着EC方向向前走 , 到达D处,又测得山顶A的仰角为
, 到达D处,又测得山顶A的仰角为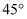 , 求山高.(结果保留根号)
, 求山高.(结果保留根号)
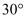 ,
,  , 自E沿着EC方向向前走
, 自E沿着EC方向向前走 , 到达D处,又测得山顶A的仰角为
, 到达D处,又测得山顶A的仰角为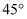 , 求山高.(结果保留根号)
, 求山高.(结果保留根号)
将一包卷卫生纸按如图所示的方式摆在水平桌面上,则它的俯视图是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是.

最近更新
- 《次北固山下》诗中的颈联是 , 。
- 少量铁粉与100mL 0.01 mol/L的稀盐酸反应,反应速率太慢。为了加快此反应速率而不改变H2的产量,可以使用如下
- In Europe many people died during the Second World War. As a
- 下列物质属于电解质而且能导电的是 ( )A、KNO3溶液 B、熔融的氯化钠 C、
- 如图所示为两球做对心碰撞前后的位移-时间图像,若m1=1kg,m2=2kg,刚刚开始运动时两球相距 米,碰撞前m1的速度
- 区域是地球表面的空间单位,它是人们在地理差异的基础上,按一定的指标和方法划分出来的,由于目的不同,所用的指标和方法也不同
- 已知数列{an}中,an=(n∈N*),则在数列{an}的前50项中最小项和最大项分别是( )A.a1 ,a50
- 小明发现冬天注满水的缸胀破了,这是因为:A.水结成冰后,质量不变,体积变大了; B.水结成冰后,质量和体积都不变
- 课内文言文部分,完成下题。 13.对下列句子中加线词语的解释,不正确的一项是( ) A.狗彘食人食而不知检 检:约
- 据《资治通鉴》记载,在贞观年间“天下大稔(丰收),流散者咸归乡里,斗米不过三四钱,终岁断死刑才二十九人。东至于海,南及五
- 若一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面的位置关系是__________________
- 两河平原是西亚的主要灌溉农业区,它主要位于( ) A.沙特阿拉伯 B.阿富汗
- 人们能看到苹果落地,却看不到规律。这是因为 A.苹果落地是现象 B.规律是人无法直接感知的 C.规律是事物运动过程
- 有关化学用语正确的是( ) A.乙烯的最简式C2H4 B.乙醇的结
- 17.下图是画家吴冠英设计的羊年生肖邮票,请结合其图像构成加以合理想象,揭示其中的寓意,不超过100字。(6分)
- There have beenmany great inventions, things that changed th
- 读下面东西半球图,其中同时被南回归线、北回归线和赤道穿过的大洲应是A.亚洲 B.大洋
- 读GPS手机界面图,界面上的时间为北京时间。如果此日全球昼夜平分,那么此地离日落还约有
- 平面六面体中,既与共面也与共面的棱的条数为 ( ) A.3 B.4 C.5
- 下列科学家与其科学成就的对应关系中不正确的是 A.伽利略——经典力学体系形成 B.牛顿——万有



