九年级(初三)数学下学期下册试题
如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )

A . (  ,2)
B . (
,2)
B . (  ,1)
C . (
,1)
C . ( 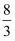 ,2)
D . (
,2)
D . ( 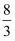 ,1)
,1)
 ,2)
B . (
,2)
B . (  ,1)
C . (
,1)
C . ( 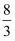 ,2)
D . (
,2)
D . ( 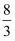 ,1)
,1)
如图,  中,
中,  ,则
,则  ( )
( )
 中,
中,  ,则
,则  ( )
( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,点O是坐标原点,△OBA∽△DOC,边OA、OC都在x轴的正半轴上.已知点B的坐标为(12,16),∠BAO=∠OCD=90°,OD=10,反比例函数的图象经过点D,交AB边于点E.

-
(1) 求该反比例函数的解析式;
-
(2) 求BE的长.
如图,⊙O的半径为1,△ABC是⊙O的内接三角形,连接OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )

A .  B . 2
B . 2  C . 3
C . 3  D . 1.5
D . 1.5 
 B . 2
B . 2  C . 3
C . 3  D . 1.5
D . 1.5 
某人沿着坡度i=  的山坡向上走了300m,则他上升的高度为 m.
的山坡向上走了300m,则他上升的高度为 m.
 的山坡向上走了300m,则他上升的高度为 m.
的山坡向上走了300m,则他上升的高度为 m. 
如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )

A . ②④
B . ②⑤
C . ③④
D . ④⑤
下列关于反比例函数 的描述中,正确的是( )
的描述中,正确的是( )
 的描述中,正确的是( )
的描述中,正确的是( )
A . 图象在二、四象限
B . 当 时,y随x的增大而减小
C . 点(
时,y随x的增大而减小
C . 点( 在反比例函数图象上
D . 当
在反比例函数图象上
D . 当 时,
时,
 时,y随x的增大而减小
C . 点(
时,y随x的增大而减小
C . 点( 在反比例函数图象上
D . 当
在反比例函数图象上
D . 当 时,
时,
数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.

计算: .
.
 .
.
计算:
-
(1)
 .
.
-
(2) 2|1﹣sin60°|+
 .
.
如图,在△ABC中,AB=AC,以AC边为直径作  O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
 O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F. 
-
(1) 求证:EF是
 O的切线;
O的切线;
-
(2) 若EB=6,且sin∠CFD=
 ,求
,求  O的半径.
O的半径.
计算  •tan 60°的值等于( )
•tan 60°的值等于( )
 •tan 60°的值等于( )
•tan 60°的值等于( )
A .  B .
B .  C .
C . 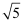 D .
D . 
 B .
B .  C .
C . 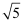 D .
D . 
从正面、左面、上面观察如图所示的几何体,分别画出你看到的几何体的形状图.

如图,在Rt△ABC中,∠ACB=90°,点D在AB上,且  =
=  .
.
 =
=  .
. 
-
(1) 求证 △ACD∽△ABC;
-
(2) 若AD=3,BD=2,求CD的长.
周末,小马和小聪想用所学的数学知识测量图书馆前小河的宽.测量时,他们选择河对岸边的一棵大树,将其底部作为点  ,在他们所在的岸边选择了点
,在他们所在的岸边选择了点  ,使得
,使得  与河岸垂直,并在
与河岸垂直,并在  点竖起标杆
点竖起标杆  ,再在
,再在  的延长线上选择点
的延长线上选择点  竖起标杆
竖起标杆  ,使得点
,使得点  与点
与点  ,
,  共线.
共线.
 ,在他们所在的岸边选择了点
,在他们所在的岸边选择了点  ,使得
,使得  与河岸垂直,并在
与河岸垂直,并在  点竖起标杆
点竖起标杆  ,再在
,再在  的延长线上选择点
的延长线上选择点  竖起标杆
竖起标杆  ,使得点
,使得点  与点
与点  ,
,  共线.
共线. 已知:  ,
,  ,测得
,测得  ,
,  ,
,  .测量示意图如图所示.请根据相关测量信息,求河宽
.测量示意图如图所示.请根据相关测量信息,求河宽  .
.

已知下图为一几何体的三视图

-
(1) 写出这个几何体的名称;
-
(2) 任意画出它的一种表面展开图;
-
(3) 若主视图的长为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积。
如图,点A、C、B是双曲线y=  (k>0,x>0) 上从右至左得三点,连结OA,OB,OC,AC,BC,△OBC和△ACO的面积相等,若A、B两点横坐标的比为4:1,则A、C两点的纵坐标的比值为。
(k>0,x>0) 上从右至左得三点,连结OA,OB,OC,AC,BC,△OBC和△ACO的面积相等,若A、B两点横坐标的比为4:1,则A、C两点的纵坐标的比值为。
 (k>0,x>0) 上从右至左得三点,连结OA,OB,OC,AC,BC,△OBC和△ACO的面积相等,若A、B两点横坐标的比为4:1,则A、C两点的纵坐标的比值为。
(k>0,x>0) 上从右至左得三点,连结OA,OB,OC,AC,BC,△OBC和△ACO的面积相等,若A、B两点横坐标的比为4:1,则A、C两点的纵坐标的比值为。

如图,反比例函数 
 图象经过
图象经过  点,
点,  轴,
轴,  ,若
,若  ,则
,则  的值为( )
的值为( )

 图象经过
图象经过  点,
点,  轴,
轴,  ,若
,若  ,则
,则  的值为( )
的值为( ) 
A . -6
B . 6
C . 3
D . -3
一次函数  的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且
的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且  △OAB的外接圆的圆心M的横坐标为-3.
△OAB的外接圆的圆心M的横坐标为-3.
 的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且
的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且  △OAB的外接圆的圆心M的横坐标为-3.
△OAB的外接圆的圆心M的横坐标为-3. 
-
(1) 求一次函数的解析式;
-
(2) 求图中阴影部分的面积.
如图,△ABC中,∠C=90°,AB=8,cosA=  ,则AC的长是.
,则AC的长是.
 ,则AC的长是.
,则AC的长是. 
最近更新
- 大气压对许多物理实验和化学实验有着重要影响。下图是喷泉实验的装置图(图中夹持装置均已略去)。(1)实验室制取氨气的化学方
- (2015·湖北宜昌中考) 如图1所示,同学们自制了一件小乐器,在8个相同的透明玻璃瓶中装有不同高度的水,用同样大小的力
- 石墨烯目前是世界上最薄、最坚硬的纳米材料,其理论厚度仅0.00000000034米,这个数用科学记数法表示为.
- How could we live without the Internet? That's how most of u
- 图,已知从A地到B地共有三条路,小红应选择第 路最近,用数学知识解释为 .
- 电视剧《大秦帝国之纵横》风靡大江南北,影片再现了秦国一统中华的历史画卷,最后完成这一历史使命的是( ) A.嬴政
- The passenger,sittingin his chair and completely______ in h
- —Have you finished your work yet? —No, I’ll finish it in ___
- 下列句子中标点符号使用有错误的一项是 A.什么是学习型社会,怎样建设学习型社会,建设学习型社会的关键是什么,一系列的问题
- (本题满分16分,第1小题4分,第2小题4分,第3小题8分) 已知函数在点(1,)处的切线方程为.
- 甲、乙两分子相距较远,设甲分子固定,而乙分子逐渐向甲靠近,直到无法再靠近,在此过程中( )A.乙总是克服分子力做功
- 阅读下面的文言文,完成4~7题。 李鄘字建侯,北海太守邕之从孙。第进士,又以书判高等补秘书省正字。李怀光辟致幕府,擢累监
- 原子序数大于4的主族元素X、Y的离子、核外电子层结构相同,则关于X、Y两元素的叙述正确的是A.X的原子序数小于Y的原子序
- 如图所示,带电平行金属板PQ和MN之间的距离为d;两板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B。如图建立坐标系,
- 填空并完成推理过程. 如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF. 解:∵∠1
- 根据对话内容及方框中所给的句子补全对话。选项中有一项是多余选项。 (Zhang Ming is from a poor
- 已知函数f(x)=ax2+bx+c的图象经过点(-1,0),是否存在常数a、b、c,使不等式x≤f(x)≤(1+x2)对
- (本题满分12分)在中,角、、的对边分别为、、,且,,边上中线的长为. (Ⅰ) 求角和角的大小;(Ⅱ) 求的面积.
- 紫茉莉花的红色(R)对白色(r)为不完全显性,下列杂交组合中,子代开红花比例最高的是 A.RR×rrB.Rr×RrC.r
- 下列各组离子在溶液中一定能大量共存的是( )A.Na+、K+、Cl- B.Ca2+、Na+、CO32- C.



