九年级(初三)数学下学期下册试题
如图,将三角形纸片  折叠,使点
折叠,使点  、
、  都与点
都与点  重合,折痕分别为
重合,折痕分别为  、
、  .已知
.已知  ,
,  ,
,  ,则
,则  的长为.
的长为.
 折叠,使点
折叠,使点  、
、  都与点
都与点  重合,折痕分别为
重合,折痕分别为  、
、  .已知
.已知  ,
,  ,
,  ,则
,则  的长为.
的长为. 
已知  中,点D在边AC上,AB=12,AC=8,AD=6,点E在边AB上,若
中,点D在边AC上,AB=12,AC=8,AD=6,点E在边AB上,若 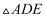 和
和  相似,则AE的长是.
相似,则AE的长是.
 中,点D在边AC上,AB=12,AC=8,AD=6,点E在边AB上,若
中,点D在边AC上,AB=12,AC=8,AD=6,点E在边AB上,若 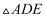 和
和  相似,则AE的长是.
相似,则AE的长是.
如图,抛物线y=-x2+k与x轴交于A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△ADC和等腰△BEC,点D,E恰好落在此抛物线上,在整个运动过程中, ∠DCE的变化情况是( )

A . 保持不变
B . 一直减小
C . 先增大后减小
D . 先减小后增大
如图所示,河堤横断面迎水坡AB的坡比是1: , 堤高BC=5m , 则坡面AB的长度是( )
, 堤高BC=5m , 则坡面AB的长度是( )
A . 10m
B . 10 m
C . 15m
D . 5
m
C . 15m
D . 5 m
m
 m
C . 15m
D . 5
m
C . 15m
D . 5 m
m
如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10  千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
 千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域. 
-
(1) 问A城是否会受到这次台风的影响?为什么?
-
(2) 若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?
某学习小组送给医务工作者的正方体6面上都有一个汉字,如图所示是它的一种展开图,那么在原正方体中,与“最”字所在面相对的面上的汉字是( )

A . 美
B . 的
C . 逆
D . 人
如图,一次函数y=  x+1的图象与轴交于点A , 与y轴交于点C , 与反比例函数y=
x+1的图象与轴交于点A , 与y轴交于点C , 与反比例函数y=  (k≠0)的图象交于B , D两点,且AC=BC .
(k≠0)的图象交于B , D两点,且AC=BC .
 x+1的图象与轴交于点A , 与y轴交于点C , 与反比例函数y=
x+1的图象与轴交于点A , 与y轴交于点C , 与反比例函数y=  (k≠0)的图象交于B , D两点,且AC=BC .
(k≠0)的图象交于B , D两点,且AC=BC . 
-
(1) 写出点A , B的坐标;
-
(2) 求出点D的坐标,并直接写出当
 >
>  x+1时,x的取值范围;
x+1时,x的取值范围;
-
(3) 若P是x轴上一点,PM⊥x轴交一次函数于点M , 交反比例函数于点N , 当O , C , M , N为顶点的四边形为平行四边形时,请直接写出点P的坐标.
如图,平面直角坐标系中,等腰Rt△ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=  (x>0)的图象上。若AB=2,则k的值为。
(x>0)的图象上。若AB=2,则k的值为。
 (x>0)的图象上。若AB=2,则k的值为。
(x>0)的图象上。若AB=2,则k的值为。 
如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.

-
(1) 当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
-
(2) 如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

-
(3) 对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).

⑴作出与△ABC关于x轴对称的△A 1B1C1 , 并写出点A1的坐标;
⑵以原点O 为位似中心,在原点的另一侧画出△A2B2C2 , 使  =
=  ,并写出点A2的坐标.
,并写出点A2的坐标.
如图,在平面直角坐标系中,  的顶点A、C的坐标分别是
的顶点A、C的坐标分别是  ,
,  ,
,  ,则函数
,则函数  的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
 的顶点A、C的坐标分别是
的顶点A、C的坐标分别是  ,
,  ,
,  ,则函数
,则函数  的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( ) 
A . 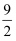 B . 9
C .
B . 9
C .  D .
D . 
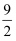 B . 9
C .
B . 9
C .  D .
D . 
如图所示,几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在△ABC中,DE∥BC,AD=2BD,则  =.
=.
 =.
=. 
如图,  中,
中,  ,点D是边
,点D是边  上的一个动点(点D与点
上的一个动点(点D与点  不重合),若再增加一个条件,就能使
不重合),若再增加一个条件,就能使 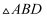 与
与  相似,则这个条件可以是(写出一个即可).
相似,则这个条件可以是(写出一个即可).
 中,
中,  ,点D是边
,点D是边  上的一个动点(点D与点
上的一个动点(点D与点  不重合),若再增加一个条件,就能使
不重合),若再增加一个条件,就能使 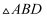 与
与  相似,则这个条件可以是(写出一个即可).
相似,则这个条件可以是(写出一个即可). 
如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形AB
CD相似,AB=4,则AD的长度为.

如图,⊙O的直径AB⊥弦CD,垂足为点E,点P在优弧CAD上(不包含点C和点D),连PC、PD、CB,tan∠BCD= 


-
(1) 求证:AE=CD;
-
(2) 求sin∠CPD.
在  中,
中,  、
、  两点分别在
两点分别在  、
、  边上,
边上, 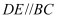 .若
.若  ,则
,则  为( )
为( )
 中,
中,  、
、  两点分别在
两点分别在  、
、  边上,
边上, 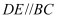 .若
.若  ,则
,则  为( )
为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,直线y=﹣x+5与双曲线y= 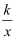 (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是 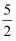 .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y=
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= 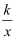 (x>0)的交点有( )
(x>0)的交点有( )
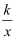 (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是 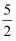 .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y=
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= 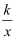 (x>0)的交点有( )
(x>0)的交点有( ) 
A . 0个
B . 1个
C . 2个
D . 0个,或1个,或2个
如图,在半径为3的圆O中,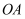 、
、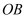 都是圆O的半径,且
都是圆O的半径,且 , 点C是劣弧
, 点C是劣弧 上的一个动点(点C不与点A、B重合),延长
上的一个动点(点C不与点A、B重合),延长 交射线
交射线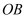 于点D.
于点D.
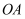 、
、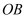 都是圆O的半径,且
都是圆O的半径,且 , 点C是劣弧
, 点C是劣弧 上的一个动点(点C不与点A、B重合),延长
上的一个动点(点C不与点A、B重合),延长 交射线
交射线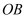 于点D.
于点D.
-
(1) 当点C为线段
 中点时,求
中点时,求 的大小;
的大小;
-
(2) 如果设
 ,
,  , 求y关于x的函数解析式,并写出定义域;
, 求y关于x的函数解析式,并写出定义域;
-
(3) 当
 时,点E在线段
时,点E在线段 上,且
上,且 , 点F是射线
, 点F是射线 上一点,射线
上一点,射线 与射线
与射线 交于点G,如果以点A、G、F为顶点的三角形与
交于点G,如果以点A、G、F为顶点的三角形与 相似,求
相似,求 的值.
的值.
定义新运算:  例如
例如  ,则函数
,则函数  的图象大致是( )
的图象大致是( )
 例如
例如  ,则函数
,则函数  的图象大致是( )
的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 古代某一学派曰:“诸侯相爱则不野战,家主相爱则不相篡,人与人相爱则不相贼,君臣相爱则惠忠,父子相爱则慈孝,兄弟相爱则和调
- 下列热化学方程式中ΔH表示可燃物标准燃烧热的是() A.CO(g)+O2(g)===CO2(g) ΔH=-283 kJ·
- 观察下面的漫画,自选角度,写一段鉴赏文字。不超过60字。(画面所题诗句为“小桌呼朋三面坐,留将一面与梅花”)(5分)
- 关于氧气用途的叙述错误的是 ( )A.氧气可用于化工生产
- 我国南方某洗衣机厂,将他们生产的洗衣机送到保险公司进行产品质量保险。每台洗衣机都放上一张“质量保险信誉证”。如果质量出了
- 下列表述与罗斯福新政相印证的是 A.“发展经济的最佳方法是自由放任,听之任之,不加干涉” B.“政府直接插手干预私营企业
- —How often do I need to feed the bird?—They ________ food ev
- . ______and ______,they ran out of room. A.Being excited;hap
- 规定“今大皇帝准将香港一岛给予大英君主暨嗣后世袭主位者常远据守主掌,任便立法治理。”这一内容的不平等条约是 A.《南京条
- 阅读下文,完成1—4题。 城市里的蟋蟀 吴丹红 和城市站在一起,也就渐渐远离了自然。“唧……唧……唧……”,那曾经是我生
- 秦九韶是我国南宋使其的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比
- 化学真正成为一门独立的学科,经历了一个漫长的历史过程.下列叙述中错误的是() A.古时候,人类发现并利用了火这一与化学有
- 在下面列举的各个实例中,机械能不守恒的是A. 汽车在水平面上匀速运动B. 抛出的手榴弹或标枪在空中的运动(不计空气阻力)
- . 第四部分: 第一节 句子翻译: 81.一种解释是:女性的嗅觉很早就得到了开发,且与识别婴儿的体味有关。
- 据天文学家测量,月球的半径为1 738 km,月球表面的重力加速度约为地球表面重力加速度的1/6,月球在阳光照射下的温度
- 现有一块表面部分被氧化为氧化钠的金属钠,其质量为1.77g,投入到100g水中产生气体0.05g。试计算:(1)钠块中钠
- 下列有关物质的鉴别方案错误的是 A.用澄清石灰水鉴别氮气和二氧化碳 B.用肥皂水鉴别硬水和软水 C.用闻气味的方法鉴别
- 春秋战国时期是我国传统农业经济形式和发展的关键时期,下列有关该时期经济发展特点的叙述正确的有( ) ①铁犁牛耕的耕作方式
- 若,则下列不等式中一定成立的是( ) A. B. C. D.
- 下列物质加入到稀硫酸中,有大量气泡产生的是( ) A.Zn B. Cu C. K2SO4



