九年级(初三)数学下学期下册试题
在光下,某建筑物的影长为24米,同时旁边3米长的标杆的影长是2米,则该建筑物的高度为( )
A . 16米
B . 18米
C . 32米
D . 36米
已知在Rt△ABC中,∠C=90°,CD⊥AB,AB=2BC,那么  的值是.
的值是.
 的值是.
的值是.
反比例函数的图象如图所示,则这个反比例函数的表达式可能是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如果反比例函数  的图象在第一、三象限,那么 k 的取值范围是( )
的图象在第一、三象限,那么 k 的取值范围是( )
 的图象在第一、三象限,那么 k 的取值范围是( )
的图象在第一、三象限,那么 k 的取值范围是( )
A . k <4
B . k≤4
C . k >4
D . k≥ 4
如图,∠MON=45°,正方形ABB1C , 正方形A1B1B2C1 , 正方形A2B2B3C2 , 正方形A3B3B4C3 , …,的顶点A , A1 , A2 , A3 , …,在射线OM上,顶点B , B1 , B2 , B3 , B4 , …,在射线ON上,连接AB2交A1B1于点D , 连接A1B3交A2B2于点D1 , 连接A2B4交A3B3于点D2 , …,连接B1D1交AB2于点E , 连接B2D2交A1B3于点E1 , …,按照这个规律进行下去,设△ACD与△B1DE的面积之和为S1 , △A1C1D1与△B2D1E1的面积之和为S2 , △A2C2D2与△B3D2E2的面积之和为S3 , …,若AB=2,则Sn等于.(用含有正整数n的式子表示)

已知反比例函数  ,下列结论错误的是( )
,下列结论错误的是( )
 ,下列结论错误的是( )
,下列结论错误的是( )
A . 图象经过点(﹣2,1)
B . 图象在第二、四象限
C . 当x<0时,y随着x的增大而增大
D . 当x>﹣1时,y>2
若两个等边三角形的边长分别为  与3
与3  ,则它们的面积之比为.
,则它们的面积之比为.
 与3
与3  ,则它们的面积之比为.
,则它们的面积之比为.
下列图形中,不能经过折叠围成正方体的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标,猜测比较合理的是 ( )
A . 小明:“早上8点”
B . 小亮:“中午12点”
C . 小刚:“下午5点”
D . 小红:“什么时间都行”
下列各点中,在函数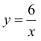 的图象上的点是( )
的图象上的点是( )
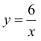 的图象上的点是( )
的图象上的点是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,△ABC中,DE∥BC,  =
=  ,则OE:OB=( )
,则OE:OB=( )
 =
=  ,则OE:OB=( )
,则OE:OB=( ) 
A . 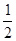 B .
B .  C .
C . 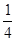 D .
D . 
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.

-
(1) 当CQ=10时,求
 的值.
的值.
-
(2) 当x为何值时,PQ∥BC;
-
(3) 是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长,若不存在,请说明理由.
如图,在淮河的右岸边有一高楼,左岸边有一坡度  的山坡
的山坡 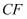 ,点
,点  与点
与点  在同一水平面上,
在同一水平面上, 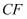 与
与  在同一平面内.某数学兴趣小组为了测量楼
在同一平面内.某数学兴趣小组为了测量楼  的高度,在坡底
的高度,在坡底  处测得楼顶
处测得楼顶  的仰角为
的仰角为  ,然后沿坡面
,然后沿坡面 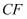 上行了
上行了  米到达点
米到达点  处,此时在
处,此时在  处测得楼顶
处测得楼顶  的仰角为
的仰角为 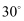 ,求楼
,求楼  的高度.(结果保留整数)(参考数
的高度.(结果保留整数)(参考数  )
)
 的山坡
的山坡 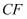 ,点
,点  与点
与点  在同一水平面上,
在同一水平面上, 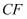 与
与  在同一平面内.某数学兴趣小组为了测量楼
在同一平面内.某数学兴趣小组为了测量楼  的高度,在坡底
的高度,在坡底  处测得楼顶
处测得楼顶  的仰角为
的仰角为  ,然后沿坡面
,然后沿坡面 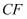 上行了
上行了  米到达点
米到达点  处,此时在
处,此时在  处测得楼顶
处测得楼顶  的仰角为
的仰角为 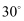 ,求楼
,求楼  的高度.(结果保留整数)(参考数
的高度.(结果保留整数)(参考数  )
) 
如图所示,该几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 D .
D . 
如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据:  ≈1.41).
≈1.41).

已知一个矩形的面积为20,若设长为a,宽为b,则能大致反映a与b之间函数关系的图象为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在Rt△ABC中,∠C=90°,各边都扩大为原来的5倍,则锐角A的三角函数值( )
A . 不变
B . 扩大5倍
C . 缩小5倍
D . 不能确定
购买  只茶杯需15元,则购买一只茶杯的单价
只茶杯需15元,则购买一只茶杯的单价  与
与  的关系式为( )
的关系式为( )
 只茶杯需15元,则购买一只茶杯的单价
只茶杯需15元,则购买一只茶杯的单价  与
与  的关系式为( )
的关系式为( )
A . 
 (
(  取实数)
B .
取实数)
B .  (
(  取整数)
C .
取整数)
C .  (
(  取自然数)
D .
取自然数)
D .  (
(  取正整数)
取正整数)
 (
(  取实数)
B .
取实数)
B .  (
(  取整数)
C .
取整数)
C .  (
(  取自然数)
D .
取自然数)
D .  (
(  取正整数)
取正整数)
下列立体图形中,俯视图可以是三角形的是( )
A . 球
B . 圆柱
C . 三棱柱
D . 长方体
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )

A .  =
= B .
B .  =
= C .
C .  =
= D .
D .  =
=
 =
= B .
B .  =
= C .
C .  =
= D .
D .  =
=
最近更新
- 下列物质中,氮元素化合价为+4价的是( ) A.NH3 B.N2 C.NO2 D.NaNO3
- .Many people were b_____________ alive under lava, ash and r
- 六价铬[Cr(Ⅵ)]有剧毒,废水中的Cr2O常用铁氧磁体法除去,即把过量的FeSO4·7H2O加入含Cr2O的废水中,调
- 在一次测量引力常量的实验中,已知一个质量为0.8 kg的球,以1.3×10-10 N的力吸引另一个质量为4.0×10-3
- 下列词语中,没有错别字的一组是 A.座落 家具 慢不经心 万事俱备 B.赊帐 取缔 指高气昂
- 我国外流区域和内流区域的河流,丰水期都在夏季,其主要原因是( ) A受气温的影响,夏季全国普遍高温B受季风影响,全国
- 为测定空气中氧气的含量,小华同学设计如下方案: 小华:采用图1装置进行实验.(燃烧匙中药品为红磷) 请回答下列问题: (
- 某有机化合物结构简式为 (1)写出其分子式____________。 (2)指出所有的官能团____________
- 2007年12月16日,国务院对外公布《全国年节及纪念日放假办法》。根据《办法》,从2008年起,全体公民放假的节日从之
- 下列词语中注音、字形有误的一项是 A.眩目(xuàn) 绥(suí)靖 锐不可当
- 二氧化氮在加热条件下能够分解成一氧化氮和氧气。该反应进行到45秒时,达到平衡(NO2浓度约为0.01 25 mol·L-
- 子房的结构包括( ) A.子房壁和胚珠 B.子房 C.花柱和柱头 D.花药和花丝
- 中共十六届三中全会强调,要把扩大就业放在经济发展更加突出的位置。中国重视就业工作体现了 ①中国共党履行经济职能
- 用4种溶液进行实验,下表中“操作及现象”与“溶液”不符的是() 选项 操作及现象 溶液 A 缓慢通入反应C+2H2O+2
- 工业上由丙烯经下列反应可制得F、G两种高分子化合物,它们都是常用的塑料。(1)聚合物F的结构简式是
- (10分)实验室为了制得少量漂白粉,常用浓盐酸与二氧化锰先制取氯气,再用氯气与消石灰反应。已知氯气与氢氧化钙制漂白粉是放
- 电冰箱的压缩机(电动机)是由温控开关控制的,当冰箱内温度达到设定温度时,压缩机开始工作。冷藏室中的照明灯是由冰箱门控制的
- 100 mL pH=2的两种一元酸x和y,稀释过程中pH与溶液体积的关系如图所示。则下列有关叙述正确的是 A.x为强酸
- 西汉期间,大力整治黄河的皇帝有( ) A.汉文帝与光武帝B.汉景帝与汉明帝 C.汉武帝与光武帝D.汉武帝与汉明帝
- 下列关于生物大分子的叙述中,不正确的是( ) A.生物大分子的主要功能是为细胞提供能量 B.核酸是储存遗传信息、控



