九年级(初三)数学下学期下册试题
如图,图中的几何体中,它的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 D .
D . 
如图是由6个大小相同的正方体搭成的几何体,下列说法正确的是( )
A . 主视图的面积最大
B . 左视图的面积最大
C . 俯视图的面积最大
D . 主视图与俯视图的面积相等
下列图形中,不是正方体表面展开图的图形的个数是 ( )

A . 1个
B . 2个
C . 3个
D . 4个
如图,已知△ABC∽△DCA,则  ==.
==.
 ==.
==.
计算: 

如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1: 的一对相似三角形;(不妨如图假设左小右大),求:
的一对相似三角形;(不妨如图假设左小右大),求:
 的一对相似三角形;(不妨如图假设左小右大),求:
的一对相似三角形;(不妨如图假设左小右大),求:(1)△BCD与△ACD的面积比;
(2)△ABC的各内角度数.

(教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.
例2 如图:在 证明:连接
|
-
(1) 请根据教材提示,结合图①,写出完整的证明过程.
-
(2) (结论应用)如图②,在
 中,D、F分别是边
中,D、F分别是边 、
、 的中点,
的中点, 、
、 相交于点G,GE
相交于点G,GE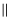 AC交
AC交 于点E,GH
于点E,GH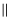 AB交
AB交 于点H,则
于点H,则 与
与 的面积的比值为.
的面积的比值为.
某型号飞机的机翼形状如图所示,根据图中数据计算 的长度(结果保留小数点后一位,
的长度(结果保留小数点后一位, ).
).
 的长度(结果保留小数点后一位,
的长度(结果保留小数点后一位, ).
). 
如图,小明从B处测得广告牌顶端A的仰角为45°,从C处测得广告牌底部D的仰角为30°,BC、AE均垂直于地面CE,已知CE=10m、BC=2m,水广告牌的高度AD.(结果保留两位小数,参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
 ≈1.414,
≈1.414, ≈1.732)
≈1.732)
如图,每个小正方形的边长为1,点A,B,C是小正方形的顶点,则∠ABC的正弦值为( )

A .  B .
B .  C .
C .  D . 不能确定
D . 不能确定
如图所示的几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
如图,在直角坐标系中, 的顶点为
的顶点为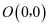 ,
,  ,
,  . 以点O为位似中心,在第三象限内作与
. 以点O为位似中心,在第三象限内作与 的位似比为
的位似比为 的位似图形
的位似图形 , 则点C的坐标为( )
, 则点C的坐标为( )
 的顶点为
的顶点为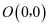 ,
,  ,
,  . 以点O为位似中心,在第三象限内作与
. 以点O为位似中心,在第三象限内作与 的位似比为
的位似比为 的位似图形
的位似图形 , 则点C的坐标为( )
, 则点C的坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知反比例函数 的图象如图所示,则一次函数
的图象如图所示,则一次函数 和二次函数
和二次函数 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
 的图象如图所示,则一次函数
的图象如图所示,则一次函数 和二次函数
和二次函数 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,点A,C在反比例函数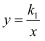 的图象上,点B,D在反比例函数
的图象上,点B,D在反比例函数 的图象上,且点A是线段OB的中点,
的图象上,且点A是线段OB的中点, 轴,
轴, 轴,
轴, 的面积是
的面积是 , 则
, 则 的值.
的值.
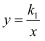 的图象上,点B,D在反比例函数
的图象上,点B,D在反比例函数 的图象上,且点A是线段OB的中点,
的图象上,且点A是线段OB的中点, 轴,
轴, 轴,
轴, 的面积是
的面积是 , 则
, 则 的值.
的值.

在探究锐角三角函数的意义的学习过程中,小亮发现:“如图1,在  中,
中,  ,可探究得到
,可探究得到  ”
”
 中,
中,  ,可探究得到
,可探究得到  ”
” 

-
(1) 请你利用图1探究说明小亮的说法是否正确;
-
(2) 小丽猜想“如果在钝角三角形中,两个锐角正弦值与它们所对边的边长之间也有一定的关系“在图2的钝角
 中,
中, 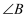 是钝角,请你利用图2帮小丽探究
是钝角,请你利用图2帮小丽探究  与
与  之间的关系,并写出探究过程.
之间的关系,并写出探究过程.
-
(3) 在锐角
 中,
中,  ,
,  ,
,  之间存在什么关系,请你探究并直接写出结论.
之间存在什么关系,请你探究并直接写出结论.
在△ABC中,∠C=90°,AB=6cm, cosB= ,则BC等于( )
,则BC等于( )
 ,则BC等于( )
,则BC等于( )
A . 1cm
B . 2cm
C . 3cm
D . 6cm
已知△ABC∽△DEF,且DE=2 cm,AB=4 cm,BC=5 cm,CA=6 cm,求△DEF的周长.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果保留根号).
如图,在高度为10米的建筑平台CD的顶部C处,测得大楼AB的顶部A的仰角α=45°,测得大楼AB的底部B的俯角β=30°,求大楼AB的高度(精确到0.1米,参考数据: ≈1.414,
≈1.414, ≈1.732).
≈1.732).
 ≈1.414,
≈1.414, ≈1.732).
≈1.732).
如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )

A . AC:BC=AD:BD
B . AC:BC=AB:AD
C . AB2=CD•BC
D . AB2=BD•BC
最近更新
- 菱形的周长为4,一个内角为60°,则较短的对角线长为A.2 B. C.1
- 下列各组给定原子序数的元素,不能形成原子数之比为1∶1稳定化合物的是 A. 3和17
- 细胞外液渗透压感受器、血糖调节中枢、体温感觉中枢分别位于( ) A.下丘脑、下丘脑、大脑皮层
- 下列选项中每组加点字的读音完全相同的一组是( ) A.复辟/辟邪着落/着手 安步当车/长歌当哭 B.供给/供认处方/处所
- These experiences are of great valuable to Tom.
- 24. “1947年年中似乎标志着战争形势的一个转折点。……军队的规模已稳步地扩大……在1947年下半年发起了全面进攻”
- 10.补写出下列名篇名句中的空缺部分。 (1) ,
- (14)设直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A、B两点,且弦AB的长为2,则a=_______
- 把含有草履虫的水倒入试管中,不久草履虫都集中在试管的上层,影响草履虫在水中这样分层分布的因素是 A.阳光
- The reason _____ which he wants to reason _____ then is stil
- 设函数f(x)=(a∈R,e为自然对数的底数).若存在b∈[0,1],使f(f(b))=b成立,则a的取值范围是() A
- 为了促进西藏经济的发展,国家投入巨资修建青藏铁路,该条铁路经过的盆地是( )A.四川盆地 B.准噶尔盆地
- 钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”。这一制度是()
- 下面的图形中,不是中心对称图形的是( ) A. B.
- 根尖吸收水和无机盐的主要部位是 A.根冠 B.分生区 C.成熟区 D.
- 2013年3月我国科学家报道了如图所示的水溶液锂离子电池体系。下列叙述错误的是()A.a为电池的正极 B.电池充电反应为
- 某实验室的光线比较暗,在使用显微镜时应选择() A.小光圈、平面镜 B.大光圈、平面镜 C.小光圈、
- 下列反应的离子方程式书写正确的是( ) A.铝和氢氧化钠水溶液反应: Al+2OH-+2H2O =AlO2-
- 阅读下面的文字,完成小题。“百度一下”张亚勤从中国科技大学少年班赴美深造,到1999年回国加盟微
- 1体积某气态烃和2体积氯化氢发生加成反应后,最多还能和6体积氯气发生取代反应。由此可以断定原气态烃是(气体体积均在相同
 相交于点G.求证:
相交于点G.求证: .
.  .
. 



