九年级(初三)数学下学期下册试题
一个几何体的三视图如图所示,则该几何体外接球的表面积为( )

A .  B .
B .  C .
C .  D .
D . 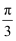
 B .
B .  C .
C .  D .
D . 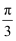
构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15°  .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( )
 .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( ) 
A .  B .
B .  ﹣1
C .
﹣1
C .  D .
D . 
 B .
B .  ﹣1
C .
﹣1
C .  D .
D . 
如图,在  中,
中,  、
、  分别是
分别是  和
和  上的点,且
上的点,且  ,如果
,如果  ,
,  ,
,  ,那么
,那么  的长是多少?
的长是多少?
 中,
中,  、
、  分别是
分别是  和
和  上的点,且
上的点,且  ,如果
,如果  ,
,  ,
,  ,那么
,那么  的长是多少?
的长是多少? 
cos60°的值等于( )
A .  B .
B . 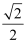 C . 1
D .
C . 1
D . 
 B .
B . 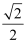 C . 1
D .
C . 1
D . 
如图坐标系中,O(0,0),A(3,3  ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=  ,则AC:AD的值是( )
,则AC:AD的值是( )
 ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=  ,则AC:AD的值是( )
,则AC:AD的值是( )

A . 1:2
B . 2:3
C . 6:7
D . 7:8
如图是反比例函数y= 的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
 的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
A . 1
B .  C . 2
D .
C . 2
D . 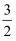
 C . 2
D .
C . 2
D . 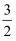
如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=  ∠P.
∠P.
 ∠P.
∠P. 
-
(1) 求证:PA是⊙O的切线;
-
(2) 若∠A=30°,⊙O的半径为4,DM=1,求PM的长;
-
(3) 如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C为顶点的三角形与△BFM相似,求DH的长度.
计算:|  -2|+2﹣1﹣cos60°﹣(1﹣
-2|+2﹣1﹣cos60°﹣(1﹣  )0.
)0.
 -2|+2﹣1﹣cos60°﹣(1﹣
-2|+2﹣1﹣cos60°﹣(1﹣  )0.
)0.
如图,有一斜坡 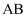 ,坡顶B离地面的高度BC为30m,斜坡AB的坡度为1:2,则此斜坡AB为( )
,坡顶B离地面的高度BC为30m,斜坡AB的坡度为1:2,则此斜坡AB为( )
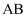 ,坡顶B离地面的高度BC为30m,斜坡AB的坡度为1:2,则此斜坡AB为( )
,坡顶B离地面的高度BC为30m,斜坡AB的坡度为1:2,则此斜坡AB为( ) 
A .  m
B . 60m
C . 30m
D . 15m
m
B . 60m
C . 30m
D . 15m
 m
B . 60m
C . 30m
D . 15m
m
B . 60m
C . 30m
D . 15m
如图所示物体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D .
已知三条线段的长分别为1.5,2,3,则下列线段中,不能与它们组成比例线段的是( )
A . l
B . 2.25
C . 4
D . 2
如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )

A . 点O
B . 点P
C . 点M
D . 点N
如图,已知双曲线y1= (x>0),y2=
(x>0),y2= (x>0),点P为双曲线y2=
(x>0),点P为双曲线y2= 上的一点,且PA⊥x轴于点A,PA,PO分别交双曲线y1=
上的一点,且PA⊥x轴于点A,PA,PO分别交双曲线y1= 于B,C两点,则△PAC的面积为( )
于B,C两点,则△PAC的面积为( )
 (x>0),y2=
(x>0),y2= (x>0),点P为双曲线y2=
(x>0),点P为双曲线y2= 上的一点,且PA⊥x轴于点A,PA,PO分别交双曲线y1=
上的一点,且PA⊥x轴于点A,PA,PO分别交双曲线y1= 于B,C两点,则△PAC的面积为( )
于B,C两点,则△PAC的面积为( )
A . 1
B . 1.5
C . 2
D . 3
校园文化艺术节上,同学们感受到浓厚的艺术氛围、体验到多彩的文化盛宴.小王同学制作了每个面上都有一个汉字的正方体,右图是它的一种展开图,那么在原正方体中,与“美”字所在面相对的面上的汉字是( )

A . 铁
B . 一
C . 同
D . 行
如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的  ,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( )
,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( )
 ,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( )
,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( ) 
A . (4,3)
B . (3,4)
C . (5,3)
D . (4,4)
如图,在  中,
中, 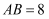 ,
,  ,点P是
,点P是  边的中点,点Q是
边的中点,点Q是  边上一动点,若
边上一动点,若  与
与  相似,则
相似,则 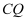 的长为.
的长为.
 中,
中, 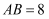 ,
,  ,点P是
,点P是  边的中点,点Q是
边的中点,点Q是  边上一动点,若
边上一动点,若  与
与  相似,则
相似,则 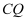 的长为.
的长为. 
已知正比例函数y=kx与比例函数  的图象都过点A(m,1).求:
的图象都过点A(m,1).求:
 的图象都过点A(m,1).求:
的图象都过点A(m,1).求:
-
(1) 正比例函数的表达式;
-
(2) 正比例函数图象与反比例数图象的另一个交点的坐标.
在一次数学活动课上,小芳到操场上测量旗杆的高度,她的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,利用她所测数据,求旗杆的高.

王师傅在楼顶上的点A出测得楼前一棵树CD的顶端C的俯角为60 , 又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )。
, 又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )。
 , 又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )。
, 又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )。
A . (24-10 )m
B . (24-
)m
B . (24-
 m
C . (24-5
m
C . (24-5 )m
D . 9m
)m
D . 9m
 )m
B . (24-
)m
B . (24-
 m
C . (24-5
m
C . (24-5 )m
D . 9m
)m
D . 9m
如图,在△ABC中(∠B≠∠C),AB=8 cm,BC=16 cm,点P从点A开始沿边AB向点B以2 cm/s的速度移动,点Q从点B开始沿边BC向点C以4 cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.

最近更新
- 中国在世界上最早培植的两种农作物是:A.棉花与水稻 B.棉花与玉米C.水稻和玉米D.水稻和粟
- —What fruit is in season now? —Grapes and peaches, ______. A
- 如图为夏季晴天某植物叶片中测得的光合作用强度的变化曲线。下列对这一曲线变化的叙述错误的是 A.AB段光合强度随光照强度增
- 正方体的棱上到异面直线,的距离相等的点的个数为( ) 2 3 4 5
- 已知物质M由同一短周期的X、Y两种元素组成,X原子的最外层电子数是最内层电子数的一半,Y元素最高正价与它的负价代数和为6
- 新文化运动产生的基本条件不包括: ( ) A.俄国十月革命的影响 B.资产
- 今年上半年,我国一些地区出现蔬菜收购价格下跌、销售不畅的现象。为减少菜农损失,各级政府采取了一些相应的措施。下列措施中,
- 肝炎病人怕吃油腻食物的原因是() A.唾液分泌过少B.胆汁分泌过少 C.胃液分泌过少D.肠液分泌过少
- 在夯实基础阶段,珠江三角洲的工业属于 A.资金密集型工业 B.技术密集型工业 C.劳动密集型工业 D.资源密
- 二甲醚(C2H6O)是一种清洁燃料,能替代柴油作车用能源,具有广阔的市场前景.下列有关二甲醚的说法错误的是( )
- (08年惠州市一模)(11分)第29届奥林匹克运动会即将在北京举办,解答下列与奥运会有关的物理学问题:(取重力加速度g=
- 关于家庭电路和安全用电,以下说法正确的是( )A. 客厅里一个开关控制四只灯泡,这四只灯泡一定是串联的。
- 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。文中共有10处语言错误,每句中最多有两处。每处错误
- 从“圆明园2010年罹难150周年纪念启动仪式”上获悉,圆明园管理处联合清华大学,将对园内的石刻文物进行大规模的保护,这
- Chinese and Nigerianmedia should pay more attention to t
- 存在于RNA而不存在于DNA,存在于叶绿体而不存在于线粒体,存在于动物细胞质中而不存在于植物细胞质中的糖类物质分别是()
- (11·漳州)口袋中有2个红球和3个白球,每个球除颜色外完全相同,从口袋中随机摸出一个红球的概率是_ ▲ .
- 假定你是李华,你的英朋友Peter来信向你咨询如何才能学好中文。请你根据以下要点写回信。 要点:1.参加中文学习班;
- 以下有关秦朝中央集权制度的说法不正确的是( ) A.是我国经济政治发展的结果 B
- Canyou imagine living without cars, computers or telephones?



