九年级(初三)数学下学期下册试题
用计算器计算:sin35°≈ (结果保留两个有效数字).
如图要测量古塔  的高度,在塔前平地上点C、D处观测塔尖A,仰角分别为
的高度,在塔前平地上点C、D处观测塔尖A,仰角分别为 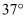 和
和  ,C、D之间的距离为21m,求古塔的高度.(结果取整数.参考数据:
,C、D之间的距离为21m,求古塔的高度.(结果取整数.参考数据:  ,
,  ,
,  )
)
 的高度,在塔前平地上点C、D处观测塔尖A,仰角分别为
的高度,在塔前平地上点C、D处观测塔尖A,仰角分别为 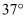 和
和  ,C、D之间的距离为21m,求古塔的高度.(结果取整数.参考数据:
,C、D之间的距离为21m,求古塔的高度.(结果取整数.参考数据:  ,
,  ,
,  )
) 
如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B, 垂直地面,垂足为点D,
垂直地面,垂足为点D, , 垂足为点C.设
, 垂足为点C.设 , 下列关系式正确的是( )
, 下列关系式正确的是( )
 垂直地面,垂足为点D,
垂直地面,垂足为点D, , 垂足为点C.设
, 垂足为点C.设 , 下列关系式正确的是( )
, 下列关系式正确的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
根据下列条件求锐角  的度数;
的度数;
 的度数;
的度数;
-
(1)
 ;
;
-
(2)
 ;
;
-
(3)
 ;
;
-
(4)
 .
.
操场上有三根测杆AB,MN和XY,MN=XY,其中测杆AB在太阳光下某一时刻的影子为BC(如图中粗线).

-
(1) 画出测杆MN在同一时刻的影子NP(用粗线表示),并简述画法;
-
(2) 若在同一时刻测杆XY的影子的顶端恰好落在点B处,画出测杆XY所在的位置(用实线表示),并简述画法.
如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m.若小芳身高只有1.2m,则她的影长为( )

A . 1.2m
B . 1.4m
C . 1.6m
D . 1.8m
三角尺在灯泡O的照射下在墙上形成的影子如图所示,OA=20cm,OA′=50cm,则这个三角尺的周长与它在墙上形成的影子的周长的比是( )

A . 5:2
B . 2:5
C . 4:25
D . 25:4
如图,已知正方形OABC的三个顶点坐标分别为A (2,0),B (2,2),C (0,2),若反比例函数  的图象与正方形OABC的边有交点,请写出一个符合条件的k值.
的图象与正方形OABC的边有交点,请写出一个符合条件的k值.
 的图象与正方形OABC的边有交点,请写出一个符合条件的k值.
的图象与正方形OABC的边有交点,请写出一个符合条件的k值. 
如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,若AC= , BC=2.则sin∠ACD的值为( )
, BC=2.则sin∠ACD的值为( )

A .  B .
B . 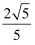 C .
C .  D .
D . 
 B .
B . 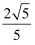 C .
C .  D .
D . 
如图,在Rt△ABC中,∠C=90°,点D在线段AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,∠B=∠BAE=30°.

-
(1) 求证:BC是⊙O的切线;
-
(2) 若AC=3,求⊙O的半径r;
-
(3) 在(1)的条件下,判断以A、O、E、F为顶点的四边形为哪种特殊四边形,并说明理由.
用计算器求下列锐角三角函数值,并填入表中:
|
锐角 |
… |
| | | | … | | | | … |
| | ||||||||||
| | ||||||||||
| |
随着锐角A的度数不断增大,  有怎样的变化趋势?
有怎样的变化趋势?  呢?
呢?  呢?你能说明自己的结论吗?
呢?你能说明自己的结论吗?
在平面直角坐标系  中,已知正比例函数
中,已知正比例函数  的图象与反比例函数
的图象与反比例函数  图象的一个交点坐标为
图象的一个交点坐标为  ,则其另一个交点坐标为.
,则其另一个交点坐标为.
 中,已知正比例函数
中,已知正比例函数  的图象与反比例函数
的图象与反比例函数  图象的一个交点坐标为
图象的一个交点坐标为  ,则其另一个交点坐标为.
,则其另一个交点坐标为.
如图,∠1=∠2,添加一个条件使得△ADE∽△ACB.

如图,  过点
过点  ,点D是y轴左侧圆上一点,则
,点D是y轴左侧圆上一点,则  的度数是( )
的度数是( )
 过点
过点  ,点D是y轴左侧圆上一点,则
,点D是y轴左侧圆上一点,则  的度数是( )
的度数是( ) 
A . 15°
B . 30°
C . 45°
D . 60°
如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

-
(1) 试说明DF是⊙O的切线;
-
(2) 若AC=3AE=6,求tanC.
计算: 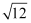 +(π﹣3.14)0×|(﹣
+(π﹣3.14)0×|(﹣  )﹣1|﹣tan60°×(﹣1)2018
)﹣1|﹣tan60°×(﹣1)2018
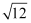 +(π﹣3.14)0×|(﹣
+(π﹣3.14)0×|(﹣  )﹣1|﹣tan60°×(﹣1)2018
)﹣1|﹣tan60°×(﹣1)2018
如图所示是一个正方体展开图,图中六个正方形内分别标有“新”、“时”、“代”、“去”、“奋”、“斗”、六个字,将其围成一个正方体后,则与“奋”相对的字是( )

A . 斗
B . 新
C . 时
D . 代
如图,在 中,
中, ,
,  ,
,  , 动点P从点A出发,沿AC以每秒2个单位长度的速度向终点C匀速运动.同时,动点Q从点C出发,沿CB以每秒1个单位长度的速度向终点B匀速运动.当点P到达终点时,点Q也随之停止运动.当点P不与点A、C重合时,连结PQ.作线段PQ的垂直平分线交折线
, 动点P从点A出发,沿AC以每秒2个单位长度的速度向终点C匀速运动.同时,动点Q从点C出发,沿CB以每秒1个单位长度的速度向终点B匀速运动.当点P到达终点时,点Q也随之停止运动.当点P不与点A、C重合时,连结PQ.作线段PQ的垂直平分线交折线 于点E,交AB于点F,交PQ于点G,连结CG.设点P的运动时间为t(秒).
于点E,交AB于点F,交PQ于点G,连结CG.设点P的运动时间为t(秒).
 中,
中, ,
,  ,
,  , 动点P从点A出发,沿AC以每秒2个单位长度的速度向终点C匀速运动.同时,动点Q从点C出发,沿CB以每秒1个单位长度的速度向终点B匀速运动.当点P到达终点时,点Q也随之停止运动.当点P不与点A、C重合时,连结PQ.作线段PQ的垂直平分线交折线
, 动点P从点A出发,沿AC以每秒2个单位长度的速度向终点C匀速运动.同时,动点Q从点C出发,沿CB以每秒1个单位长度的速度向终点B匀速运动.当点P到达终点时,点Q也随之停止运动.当点P不与点A、C重合时,连结PQ.作线段PQ的垂直平分线交折线 于点E,交AB于点F,交PQ于点G,连结CG.设点P的运动时间为t(秒).
于点E,交AB于点F,交PQ于点G,连结CG.设点P的运动时间为t(秒).
-
(1) 用含t的代数式表示线段CP的长度为.
-
(2) 当PQ与AB平行时,求t的值.
-
(3) 当
 是等腰三角形时,求t的值.
是等腰三角形时,求t的值.
-
(4) 当
 时,直接写出t的值.
时,直接写出t的值.
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )

A . 175π+450
B . 700π+450
C . 700π+1500
D . 250π+1050
西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.

最近更新
- 下列说法中不正确的是()。A. 糖类、油脂、蛋白质都是人体必需的营养物质B. 农业上大量使用杀虫剂以提高农作物产量C.
- 偶函数f(x)在[-1,0]上为单调递减函数,又α、β为锐角三角形的两个内角,则有( )A.f(cosα)>f(c
- 下列句子中没有错别字的一句是( ) A、前扑后继 邂逅 披星带月 化干戈为玉帛 B、心心
- 纽扣电池可作计算器、电子表等的电源。有一种纽扣电池,其电极分别为Zn和Ag2O,用KOH溶液作电解质溶液,电池的总反应为
- 历史上很多著名的科学家同时也是哲学家,例如伽利略、笛卡尔、爱因斯坦等,也有很多著名的哲学家 同时也是科学家,例如培根、莱
- 西瓜之所以甘甜可口,主要是因为西瓜的 含有大量的糖分 ()A.细胞壁 B.细胞膜 C.细胞液 D.细胞
- 民主革命时期,中国领导人民军队打了无数胜仗。下列战役发生在解放战争时期的是 A.四渡赤水 B.
- (08年德州市质检理) 定义运算“*”如下:a*b=,则函数的最大值等于
- 不能用水浴加热的实验是( )A.苯的硝化反应 B.银镜反应 C.制酚醛树脂
- 2014年5月9日,经湖南省纪委研究并报湖南省委同意,决定对衡阳破坏选举案(见图)中部分违反党纪政纪人员共409人给予党
- 以下温度最接近25℃的是 ( )
- (09广东卷)3.水稻细胞内合成的某物质,能够在常温下高效分解淀粉,该物质 A. 在4℃条件下易变性
- 正三棱锥的侧面均为直角三角形,则它的侧面与底面所成角的余弦值是_____________.
- 下图是一个细胞的亚显微结构模式图。根据图回答问题(在横线上写出细胞或结构的名称,在括号内写标号):(1)该图是
- 如果两个遗传性状发生重组,说明控制这两个性状的基因有如下可能关系:A.独立遗传 B.不完全连锁 C.完全连锁 D.细胞质
- 同一短周期的元素W、X、Y、Z的原子序数依次增加,下列叙述不正确的是:A.单质的化学活泼性:W<X<Y&l
- 抛物线的焦点坐标是 .
- 科学家在细胞中发现了一种新的线粒体因子——MTERF3,这一因子主要抑制线粒体DNA的表达,从而减少细胞能量的产生。此项
- 下图一表示人体吸收葡萄糖的过程示意图,图二表示人体内离子通道的三种类型。有关叙述不正确的是( )A.图一中①和②处Na+
- —Hey, dad. ______ —I can’t find my glasses. A. How are y