九年级(初三)数学下学期下册试题
关于反比例函数 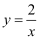 的图象和性质,下列说法错误的是( )
的图象和性质,下列说法错误的是( )
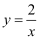 的图象和性质,下列说法错误的是( )
的图象和性质,下列说法错误的是( )
A . 函数图象关于原点对称
B . 函数图象分别位于第一、三象限
C . 点(﹣1,﹣2)在函数图象上
D . 当x>0时,y随x的增大而增大
如图,已知在△ABC中,点D,E分别在边AB,AC上,DE∥BC,AD:BD=2:1,点F在AC上,AF:FC=1:2,联结BF,交DE于点G,那么DG:GE等于( )

A . 1:2
B . 1:3
C . 2:3
D . 2:5.
如图,在  中,点
中,点  在边
在边  上,连接
上,连接  并延长交
并延长交  的延长线于点
的延长线于点  ,若
,若  ,则
,则  .
.
 中,点
中,点  在边
在边  上,连接
上,连接  并延长交
并延长交  的延长线于点
的延长线于点  ,若
,若  ,则
,则  .
. 
构造几何图形解决代数问题是“数形结合思想”的重要应用,小康在计算  时,构造出如图所示的图形:在Rt
时,构造出如图所示的图形:在Rt  ACD中,
ACD中,  ,
,  ,延长
,延长 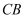 到
到  ,
,  ,连接
,连接  ,得
,得  .根据此图可求得
.根据此图可求得  的结果( )
的结果( )
 时,构造出如图所示的图形:在Rt
时,构造出如图所示的图形:在Rt  ACD中,
ACD中,  ,
,  ,延长
,延长 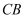 到
到  ,
,  ,连接
,连接  ,得
,得  .根据此图可求得
.根据此图可求得  的结果( )
的结果( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
对新城初中某年级学生的体重(单位:kg,精确到1kg )情况进行了抽查,将所得数据处理后分成A,B,C三组(每组含最低值,不含最高值),并制成如图1、表1的统计图表(部分数据未填),在被抽查的学生中偏瘦和偏胖的学生共有.


如图,已知点P是△ABC的重心,过P作AC的平行线DE,分别交AB于点D、交BC于点E;作DF∥BC,交AC于点F,若S△ABC=18,则S四边形ECFD=.

反比例函y=﹣ 的图象位于( )
的图象位于( )
 的图象位于( )
的图象位于( )
A . 第一、三象限
B . 第二、四象限
C . 第一、四象限
D . 第二、三象限
如图,  和
和  都是等腰直角三角形,
都是等腰直角三角形, 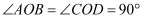 ,且点
,且点  、
、  、
、  在同一条直线上,连接
在同一条直线上,连接  .
.
 和
和  都是等腰直角三角形,
都是等腰直角三角形, 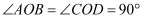 ,且点
,且点  、
、  、
、  在同一条直线上,连接
在同一条直线上,连接  .
. 
-
(1)
 的度数为.
的度数为.
-
(2) 若
 、
、  分别是
分别是  、
、  的中点,连接
的中点,连接  ,
, 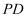 ,
,  ,则
,则  的值为.
的值为.
一个几何体从正面、左面、上面看都是同一平面图形的几何体有、。(写两种即可)
五个大小相同的正方体搭成的几何体如图所示,其左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若  的每条边长增加各自的
的每条边长增加各自的  得
得  ,则
,则  的度数与其对应角
的度数与其对应角 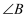 的度数相比( )
的度数相比( )
 的每条边长增加各自的
的每条边长增加各自的  得
得  ,则
,则  的度数与其对应角
的度数与其对应角 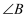 的度数相比( )
的度数相比( )
A . 增加了  B . 减少了
B . 减少了  C . 增加了
C . 增加了  D . 没有改变
D . 没有改变
 B . 减少了
B . 减少了  C . 增加了
C . 增加了  D . 没有改变
D . 没有改变
如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:  (即AB:BC=1:
(即AB:BC=1:  ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
 (即AB:BC=1:
(即AB:BC=1:  ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
-
(1) 用适当的方法解方程:3(x-1)2=2(x-1)
-
(2) 计算:

如图,点A在反比例函数 的图象上,点C在x轴的正半轴上,AC交y轴于点B,若
的图象上,点C在x轴的正半轴上,AC交y轴于点B,若 ,
,  的面积为1,则
的面积为1,则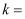 .
.
 的图象上,点C在x轴的正半轴上,AC交y轴于点B,若
的图象上,点C在x轴的正半轴上,AC交y轴于点B,若 ,
,  的面积为1,则
的面积为1,则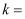 .
.
如图,以  的边
的边  为直径的
为直径的  交
交  于点F , 点E是
于点F , 点E是  的中点,连接
的中点,连接  并延长交
并延长交  于点D , 若
于点D , 若  .
.
 的边
的边  为直径的
为直径的  交
交  于点F , 点E是
于点F , 点E是  的中点,连接
的中点,连接  并延长交
并延长交  于点D , 若
于点D , 若  .
. 
-
(1) 求证:
 是
是  的切线;
的切线;
-
(2) 若
 的半径为2,
的半径为2,  ,求
,求  的长.
的长.
计算:﹣14+ 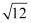 +sin60°+(π﹣
+sin60°+(π﹣ 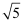 )0=.
)0=.
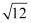 +sin60°+(π﹣
+sin60°+(π﹣ 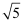 )0=.
)0=.
如图,直角坐标系中,P(3,y)是第一象限内的点,且 , 求sinα.
, 求sinα.
 , 求sinα.
, 求sinα.
下列各组数中,能成比例的是( )
A . 3,4,5,6
B . -1,-2, 2,4
C . -3,1,3,0
D . -1,2,-3,4
已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.

-
(1) 请你添加一个适当的条件,使得四边形ABCD是平行四边形,并证明你的结论;
-
(2) 作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
-
(3) 在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=
 ,求⊙O的半径.
,求⊙O的半径.
如图所示的几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
最近更新
- 文学类文本阅读(25分)兄弟赵宏欣街心公园里,有一片针松林。说是林,其实也不怎么算林,也就那么七、八棵树。不过,那树大约
- 下列加点字注音全部正确的一项是( )(3分) A.亵(xiè)渎 滞(zì)笨 鲜(xiān)为人知 B.
- 如图所示,通电螺线管左端是 极。(填“N”或“S”)
- 已知酸性条件下有如下反应:2Cu+===Cu2++Cu。由于反应温度不同,用氢气还原氧化铜时,可能产生Cu或Cu2O,两
- 某一年,农民甲开展多种经营,承包土地年收入3万元,利用业余时间炒股嫌得2万元,用自己的私家货车跑运输得到报酬4万元。那么
- 某材料显示:清前期,景德镇民窑接受欧洲人的定制,并经由荷兰人运往欧洲,器型种类包括西式餐具或人物饰像等。对于该材料的解读
- 从下图《变动着的市场价格》可以得出的合理结论有 ①如果高档耐用品在N点,其替代产品需求量增加②如果生活必需品在M点,
- 肉毒碱(化学式为C7H15NO3)是一种具有多种生理功能的物质,被公认为人体必需的营养物质和最佳的减肥营养素。下列关于
- 下列实验基本操作中正确的是 A.闻气味 B.熄灭酒精灯C.滴加液体D.倾倒液体
- 完形填空。 “Nancy,try to cook for us today,” my mother called.“Bu
- 现代类人猿和人类的共同祖先是( ) A.东非人 B.森林古猿 C.长臂猿 D.北京人
- 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,
- 细菌相对于真菌,明显不同的特点是( ) A.能分解动植物遗体
- 下列措施不合理的是()A.用SO2漂白纸浆和草帽辫 B.用硫酸清洗锅炉中的水垢 C.高温下用焦
- 下列各句中,没有语病的一句是 A、有关部门对极少数不尊重环卫工人劳动、无理取闹的事件,及时进行了批评教育和严肃处理。
- 右图是耸立在国家博物馆北广场的孔子青铜雕像,它成为天安门地区的文化新地标。下列有关孔子的说法不符合史实的是A.春秋时期鲁
- 下图为我国某区域多年平均气温分布图(单位:℃),读图回答下面试题。 影响图示地区气温分布的主要因素是 A.纬度因素
- 21.下列叙述正确的是()A.同周期元素中,ⅦA族元素的原子半径最大B.ⅥA族元素的原子,其半径越大,越容易得到电子C.
- 如图所示,当神经冲动在轴突上传导时,下列叙述错误的是 A.丁区域发生K+外流和Na+内流 B.甲区与丙区可能刚恢复为静息
- 皇帝主要通过奏事、朝议、刺察等形式掌握全国的军政信息,控制和指挥着整个国家机器的运转。秦朝时期能够参加朝议的官员不包括



